 学生の方
学生の方数Bの確率って、文字とかグラフとか出てきてわかりにくい…
「数学B」で習う確率分布と統計的な推測。
数学Aで習った確率の延長ですが、
確率変数、期待値、分散、二項分布、正規分布など、新しい用語が出てきたり、グラフを使って解く問題があったりして難しそう…と思っていませんか?
実は、数Bの確率の単元は、一度覚えてしまえば、問題のパターンはかなり限られているので、早く得点に繋げることができます。
この記事では、数Bの確率の基礎となる、確率変数、期待値、分散の意味と求め方をわかりやすく説明していきます。
解き方をしっかり覚えて、得点源にしていきましょう!



粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

確率変数と確率分布
確率変数
確率変数とは、サイコロを振って出た目の数とか、くじを10回引いてあたりが出た回数のような、確率の問題でよくやる試行の結果として出てくる数字のことです。
普通はXとかYとかの文字で表されます。
普通は問題文に「サイコロを振って出た目の数をXとする」とか書いてあるので、それに従えばいいです。
確率の記号
「サイコロを振って3が出る確率」って毎回日本語で書いてると面倒なので、記号で表します。
サイコロを振って出た目の数をXとするとき、X=3となる確率は、記号で、
P(X=3)
と書きます。このPはprobability(確率)の頭文字からとられています。
また、( )の中は不等式を入れることもできます。
例えばサイコロを振って2以上4以下の目が出る確率は、
P(2\leqq X \leqq 4)
のように書きます。
確率分布
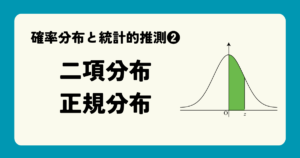
確率分布とは、確率変数と、それが起こる確率を対応させたものです。
例えばサイコロを1回振って出る目をXとすると、それぞれの目が出る確率は\cfrac{1}{6}ずつなので、Xの確率分布は次の表のようになります。
もうひとつ例を。
コインを2枚投げると、表と裏の出方は、
(表,表),(表,裏),(裏,表),(裏,裏)
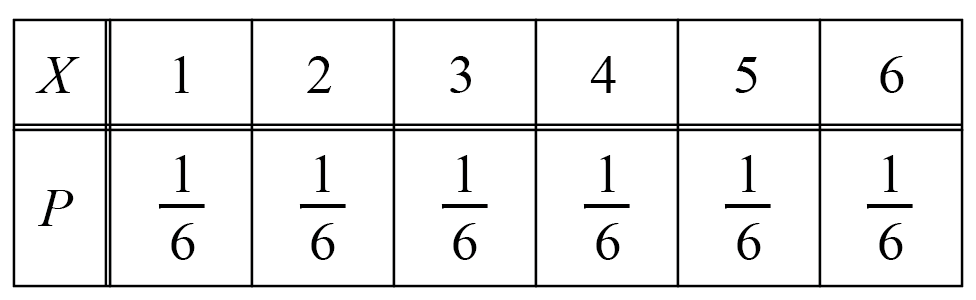
の4通りがあります。ここで、表の枚数をXとすると、
X=0になるのは(裏,裏)の1通りで、
確率は\cfrac{1}{4}
X=1になるのは(表,裏)と(裏,表)の2通りで、
確率は\cfrac{2}{4}=\cfrac{1}{2}
X=2になるのは(表,表)の1通りで、
確率は\cfrac{1}{4}
になるので、Xの確率分布は次のようになります。
期待値と分散
数Bの確率は、個別の確率を求める計算そのものはとても簡単になっている場合が多いので、数Aでやった確率の基本的なものができていれば、あまり心配はありません。
数Bでは、確率を求めたあとの計算がメインになっていきます。
まずは期待値と分散の計算です。
期待値
期待値とは、「確率変数×確率」の合計です。
別名を「平均」ともいうので、1回あたりの確率変数の平均と考えてもいいでしょう。
「Xの期待値」は、expectation(期待値)の頭文字をとって、E(X) と書きます。
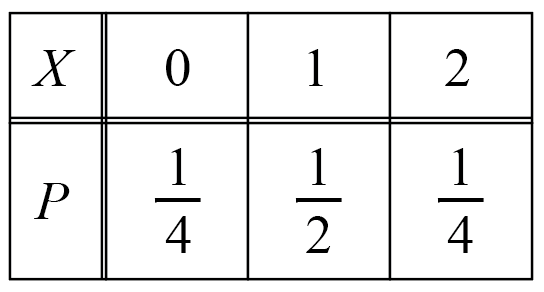
例えば、1000本のくじがあって、賞金と本数が次のようになっているとします。
もらえる賞金額をX円とすると、Xの確率分布は次のようになります。
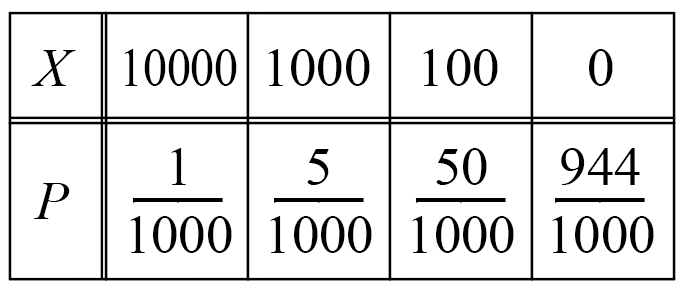
そして、XとPをかけて全部足すと期待値になるので、
E(X)=10000\cdot\cfrac{1}{1000}+1000\cdot\cfrac{10}{1000}+100\cdot\cfrac{50}{1000}+0\cdot\cfrac{944}{1000}=20よって期待値は20円。
つまり,1回引いて期待できる賞金額の平均は20円ということになります。
 粗茶さん
粗茶さんくじの料金が20円よりも高い場合は、引かないほうがいいってこと。
別の例を1つ。
サイコロを1回振って出た目の数をXとするとき、Xの期待値を求めよ。
先程もやりましたが、確率分布はこんな感じ。

なので、Xの期待値は、
E(X)=1\cdot\cfrac{1}{6}+2\cdot\cfrac{1}{6}+3\cdot\cfrac{1}{6}+4\cdot\cfrac{1}{6}+5\cdot\cfrac{1}{6}+6\cdot\cfrac{1}{6}=\cfrac{7}{2}となります。
サイコロの場合はすべてのXに対応する確率が等しいですね。
このように、確率に何らかの法則があるときは、もうちょっとかっこよくシグマで計算することもできます。
 粗茶さん
粗茶さん数列が苦手な人は、飛ばしても大丈夫ですよ。
E(X)=\displaystyle{\sum^{6}_{k=1}}\left(k\cdot\cfrac{1}{6}\right)=\cfrac{1}{6}\displaystyle{\sum^{6}_{k=1}}k=\cfrac{1}{6}\times\cfrac{1}{2}\cdot6\cdot7=\cfrac{7}{2}一般的に
P(X=x_1)=p_1,P(X=x_2)=p_2,…,P(X=x_n)=p_n
のとき、
E(X)=x_1p_1+x_2p_2+\cdots+x_np_n=\displaystyle{\sum^n_{k=1}x_kp_k}って書くことができます。
aX+bの期待値
確率変数に数字をかけたり足したりしたものも、確率変数として扱うことができます。
サイコロを1回振って出た目の数をXとするとき、2X+3の期待値を求めよ。
出た目を2倍して3を足したものを、新しい確率変数として、期待値を計算します。
とりあえず確率分布はこんな感じ。
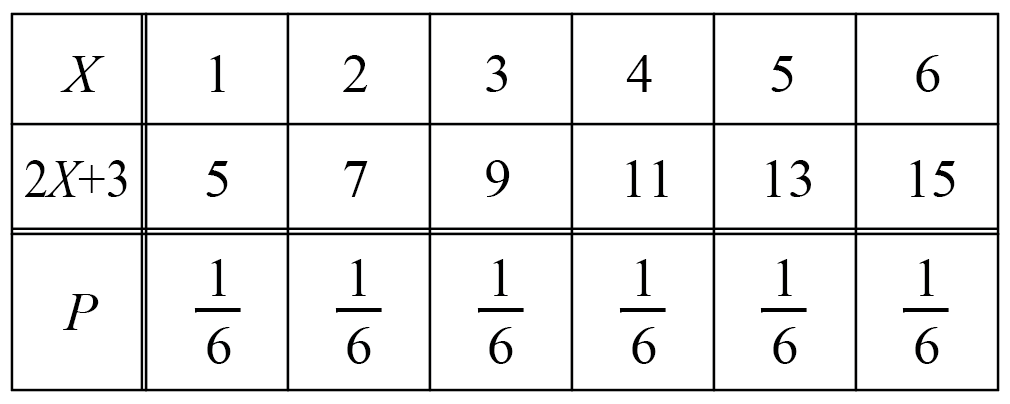
なので、2X+3の期待値は、
\begin{array}{ll}
&E(2X+3)\\\\
=& 5\cdot\cfrac{1}{6}+7\cdot\cfrac{1}{6}+9\cdot\cfrac{1}{6}+11\cdot\cfrac{1}{6}+13\cdot\cfrac{1}{6}+15\cdot\cfrac{1}{6}\\\\
=&10
\end{array}これで問題ないんですが、事前にE(X)が出ている場合は、次の公式が利用できます。
Xを確率変数,a,bを定数とするとき,
E(aX+b)=aE(X)+b
全員の点数がa倍されれば、平均もa倍になるし、全員の点数がb増えれば、平均もb増えるに決まっているので、当たり前です。
これを使うと、例題2の期待値は、E(X)=\cfrac{7}{2}を利用して、
\begin{array}{ll}
&E(2X+3)\\\\
=&2E(X)+3\\\\
=&2\cdot\cfrac{7}{2}+3\\\\
=&10
\end{array}と求めることができます。
共通テストでもよく出てくるのでサクッとできるようにしておきましょう。
分散
1,2,3,4,5,6の目があるサイコロを1回振って出る目の期待値は\cfrac{7}{2}でした。
もしサイコロの目が3,3,3,4,4,4の6つだった場合でも、期待値は3\cdot\cfrac{1}{2}+4\cdot\cfrac{1}{2}=\cfrac{7}{2}になります。
両者は期待値が同じですが、分布の仕方が異なります。
1から6の目があるサイコロは、期待値に近い値もあれば遠い値もあって、バラツキが大きいです。
一方3と4しかないサイコロは、期待値の付近に値が集中していて、バラツキが小さくなっています。
このように、確率変数の散らばり具合を表す値に、分散があります。
分散は、「(X-期待値)^2\times確率」の合計 で求められます。
 粗茶さん
粗茶さん2乗しないと最終的な答えが0になっちゃうので、2乗したあとに確率をかけます。
「Xの分散」は、variance(分散)の頭文字をとって、V(X) と書きます。
コインを2枚投げて、表が出る枚数をXとするとき、Xの分散を求めよ。
上の方でもやっていますが、確率分布はこんな感じでした。

これより、期待値は、
E(X)=0\cdot\cfrac{1}{4}+1\cdot\cfrac{1}{2}+2\cdot\cfrac{1}{4}=1分散は「(X-期待値)^2\times確率」の合計 だったので、
V(X)=(0-1)^2\cdot\cfrac{1}{4}+(1-1)^2\cdot\cfrac{1}{2}+(2-1)^2\cdot\cfrac{1}{4}=\cfrac{1}{2}分散は、別の求め方があります。
確率変数Xについて,
V(X)=E(X^2)-\{E(X)\}^2つまり、(分散)=(2乗の期待値)ー(期待値の2乗)ということです。
証明は一応書いておきますが、あまり重要ではないので、興味のある人は見てください。
分散公式の証明(クリックで表示)
X=x_nとなる確率をp_n,期待値をmとすると、分散は、
\begin{array}{ll}
&(x_1-m)^2p_1+(x_2-m)^2p_2+\cdots+(x_n-m)^2p_n\\\\
=&({x_1}^2p_1-2mx_1p_1+m^2p_1)+({x_2}^2p_2-2mx_2p_2+m^2p_2)+\cdots+({x_n}^2p_n-2mx_np_n+m^2p_n)\\\\
=&{\color{red}{x_1}^2p_1+{x_2}^2p_2\cdots{x_n}^2p_n}+-2m({\color{blue}x_1p_1+x_2p_2+\cdots+x_np_n})+m^2({\color{green}p_1+p_2+\cdots+p_n})
\end{array}ここで、赤の部分はX^2の期待値なのでE(X^2)、青の部分はXの期待値なのでE(X)、緑の部分はすべての確率の和なので1になる。ついでにm=E(X)でもあるので、この式は、
\begin{array}{ll}
&{\color{red}E(X^2)}-2E(X){\color{blue}E(X)}+\{E(X)\}^2\cdot {\color{green}1}\\\\
=&E(X^2)-\{E(X)\}^2\end{array}で、どちらの方法でも分散を出すことができるのですが、一応の使い分けは次のようになります。
- 期待値が整数のとき…「(X-期待値)^2\times確率」の合計
- 期待値が分数のとき…(2乗の期待値)ー(期待値の2乗)
期待値が整数の場合は、「(X-期待値)^2」が整数になりやすいので、分散は上の方法で求めやすいです。
期待値が分数(整数でない)場合は、「(X-期待値)^2」の計算が面倒なので、下の方法でやったほうがまだマシです。
状況に応じて使い分けられるように、両方のやり方を覚えておきましょう。
標準偏差
標準偏差とは,分散にルートをつけたものです。
分散は、計算のときに2乗が行われているので、数字が大きくなりすぎてしまって扱いにくいことがあるので、実際の単位に近づけるために、ルートをつけたのが標準偏差。ぐらいの認識でいいです。
「Xの標準偏差」は、standard deviation(標準偏差)の頭文字のsに相当するギリシャ文字\sigma(シグマ)を使って、\sigma(X)と表します。なぜかこれだけギリシャ文字。
例題3におけるXの標準偏差は、
\sigma(X)=\sqrt{V(X)}=\cfrac{1}{\sqrt{2}}ということになります。
aX+bの分散と標準偏差
期待値と同じように,aX+bの分散と標準偏差を求める機会があります。
具体的には次の公式になります。
Xを確率変数,a,bを定数とするとき,
\begin{array}{l}
V(aX+b)=a^2V(x),
\sigma(aX+b)=|a|\sigma(X)
\end{array} 学生の方
学生の方+bはどこいったの?
という気持ちになったと思いますが,全員がb点アップしても,全体が平行移動するだけで,散らばり具合は変わらないので,+bは,分散や標準偏差に影響を与えません。
一方aについては,2乗の計算の影響を受けるので,分散はa^2倍,標準偏差はその平方根で|a|倍になります。
詳しい証明が気になる方は,ご覧ください。
aX+bの分散の計算(クリックで表示)
\begin{array}{ll}
&V(aX+b)\\\\
=&\{(ax_1+b)-E(aX+b)\}^2p_1+\cdots+\{(ax_n+b)-E(aX+b)\}^2p_n
\end{array}期待値E(aX+b)は,aE(X)+bでした。
そしてE(X)=mとすると,この式は,
\begin{array}{ll}
&\{(ax_1+b)-(am+b)\}^2p_1+\cdots+\{(ax_n+b)-(am+b)\}^2p_n\\\\
=&\{a(x_1-m)\}^2p_1+\cdots+\{a(x_n-m)\}^2p_n ※ここでbが消える\\\\
=&a^2(x_1-m)^2p_1+\cdots+a^2(x_n-m)^2p_n\\\\
=&a^2\{{\color{red}(x_1-m)^2p_1+\cdots+(x_n-m)^2p_n}\}
\end{array}赤色の部分は,Xの分散V(X)になっているので,求める分散は,
a^2V(X) になります。
また,
\begin{array}{ll}
&\sigma(aX+b)\\\\
=&\sqrt{V(aX+b)}\\\\
=&\sqrt{a^2V(X)}\\\\
=&|a|\sigma(X)
\end{array} 粗茶さん
粗茶さん\sqrt{a^2}は a じゃなくて |a|ですよ。
この公式もよく使われるので,しっかり使えるようにしておきたいですね。
確率変数と期待値と分散 まとめ
ということで,今回は確率変数・期待値・分散のお話でした。
覚えておくことは,
- 確率変数Xとは,試行の結果として得られる値のこと
- 期待値E(X)は,確率変数×確率 の合計
- E(aX+b)=aE(X)+b
- 分散V(X)は,(X−期待値)^2\times確率の合計,または(2乗の期待値)ー(期待値の2乗)
- 標準偏差\sigma(X)は,分散の平方根
- V(aX+b)=a^2(X),\sigma(aX+b)=|a|\sigma(X)
でした。
数Ⅰでやっている「データの分析」でも同じようなことを学んでいると思うので,なじみやすかったでしょうか?
数Bの確率統計の問題を解く上での基本事項になるので,しっかりマスターしておきましょう。
確率変数の次は,有名な分布の種類や統計的推測についても学びましょう。


オススメ参考書
数Bの確率を扱っている参考書は数少ないですが,おすすめはこちら。
なんと楽天kobo電子書籍版もあります。
このブログでは,自分で勉強しているとき,つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や,勉強が楽しくなる文房具も紹介していますので,よろしければご覧ください!




