数Bの確率統計シリーズの3回目です。
今回は統計的な推測の部分をやります。
特に母平均の推定・母比率の推定は、共通テストでもメインとなる部分ですので、流れをしっかり抑えて得点源にしてほしいです!



粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。
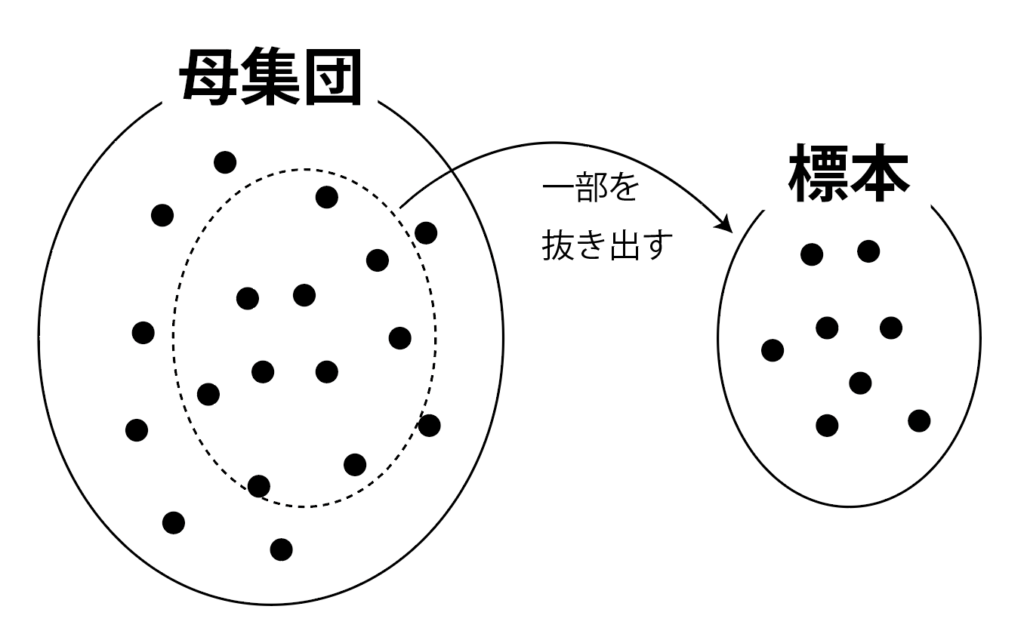
母集団と標本
統計的な調査をするときは,調べたい対象全部を調べる全数調査と,一部を抜き出して調べて,そこから全体の様子を推測する標本調査があります。
全数調査
5年に1回やっている国勢調査は,全数調査の代表例です。
全数調査は,対象全体の状況を正確に知ることができる反面,時間や労力がかかって大変です。
標本調査
一方,標本調査は,少ない時間や労力でできますが,対象全体の状況を完全に正確に把握することはできません。
ですが,標本調査が使われる場面は多くあります。
例えば,工場の製品を検査する場合は,全部の製品を傷つけるわけにはいかないので,標本調査が行われています。
標本調査では,調べたい対象全体の集合を母集団,調査のために母集団から抜き出された(抽出された)要素の集合を標本といいます。
また,母集団の各要素を等しい確率で抽出する方法を無作為抽出といい,無作為抽出によって選ばれた標本を無作為標本といいます。
 粗茶さん
粗茶さん標本が極端にかたよったものになると困るからね。
標本平均とその分布
ここからは,標本平均と分布について考えていきます。
標本平均と標本標準偏差
例えば,全校生徒1000人の学校で,生徒の身長の平均を知りたい場合を考えます。
1000人をの平均を計算するのは多すぎてつらいので,20人を無作為に抽出して調べることにしました。
この20人の集合が標本ですね。
抽出した数(今回は人数)のことを標本の大きさというので,今回の場合は,
「母集団から大きさ20の標本を無作為に抽出した」
と表現します。
この20人の身長を順に X_1,X_2,\cdots,X_{20}
として,その平均を\overline{X} とすると,
\overline{X}=\cfrac{1}{20}(X_1+X_2+\cdots +X_{20})
これを標本平均といいます。
また, X_1,X_2,\cdots,X_{20} の分散 S^2 は,
S^2=\cfrac{1}{20}\left\{(X_1-\overline{X})^2+(X_2-\overline{X})^2+\cdots+(X_{20}-\overline{X})^2\right\}
これにルートをつけると標準偏差 S になるってことで,
S=\sqrt{\cfrac{1}{20}\left\{(X_1-\overline{X})^2+(X_2-\overline{X})^2+\cdots+(X_{20}-\overline{X})^2\right\}}
これを標本標準偏差といいます。
今の説明は標本の大きさが20でしたが,一般に標本の大きさ n でいえることなので,まとめると,
母集団から大きさ n の標本を無作為に抽出し,変量 x について,その標本のもつ x の値を X_1,X_2,\cdots,X_n とするとき,
\overline{X}=\cfrac{1}{n}(X_1+X_2+\cdots+X_n)
を標本平均といい,
S=\sqrt{\cfrac{1}{n}\left\{(X_1-\overline{X})^2+(X_2-\overline{X})^2+\cdots+(X_{n}-\overline{X})^2\right\}}
を標本標準偏差という。
※標本平均や標本標準偏差に対して,母集団の平均を母平均(通常は m で表す),母集団の標準偏差を母標準偏差(通常は \sigma で表す)といいます。
標本平均の期待値と標準偏差
先程,1000人の生徒から無作為にに20人を抽出して標本を作りましたが,抽出を行うたびに別の20人が選ばれるので,その都度標本平均は変わりますよね。
その,毎回変わる標本平均の値の平均(期待値)は,どんな値になるのかな?また,標本平均の標準偏差はどんな値になるのかな?ということを考えていきます。
 粗茶さん
粗茶さん「標本」の期待値ではなくて,「標本平均」の期待値です!
母平均 m,母標準偏差 \sigma である母集団から大きさ n の標本を抽出するときの,標本平均の期待値と標準偏差を考えます。
まずは標本平均の期待値です。素直に計算してみましょう。
E(\overline{X})
=E\left(\cfrac{X_1+X_2+\cdots+X_{n}}{n}\right)
=\cfrac{1}{n}E(X_1+X_2+\cdots+X_{n})
=\cfrac{1}{n}\left\{E(X_1)+E(X_2)+\cdots+E(X_{n})\right\}
ここで E(X_1)というのは,身長で言えば,「母集団から1番目に抽出される人の身長X_1の期待値(平均)」という意味です。
平均 m の母集団から抽出するので,当然 X_1 の平均(期待値)も m です。
X_2 以降も同じことなので,
E(X_1)=E(X_2)=\cdots=E(X_n)=m
が成り立ちます。
それでは式の続きをどうぞ。
=\cfrac{1}{n}(m+m+\cdots m)
=\cfrac{1}{n}\cdot nm
=m
ということで,標本平均の期待値は,母平均と同じになります。
つづきまして,標本平均の標準偏差も求めてみましょう。素直に計算するよ。
 粗茶さん
粗茶さんVは分散です。
\sigma(\overline{x})=\sqrt{V(\overline{X})}
=\sqrt{V\left(\cfrac{X_1+X_2+\cdots+X_n}{n}\right)}
=\sqrt{\cfrac{1}{n^2}V(X_1+X_2+\cdots+X_n)}
 粗茶さん
粗茶さん\cfrac{1}{n}倍された変量の分散は,もとの変量の分散の\cfrac{1}{n^2}倍
=\sqrt{\cfrac{1}{n^2}\left\{V(X_1)+V(X_2)+\cdots+V(X_n)\right\}}
 粗茶さん
粗茶さんX_1,X_2,\cdots,X_nは独立なので,分散はそれぞれ分けてOK
X_1,X_2,\cdots,X_n は,母集団から抽出している以上,母集団の分布に従うので,期待値だけでなく,標準偏差も母標準偏差と同じと考えられる。つまり,
\sigma(X_1)=\sigma(X_2)=\cdots=\sigma(X_n)=\sigma
がなり立ちます。もちろん分散も母集団の分散(\sigma^2)と同じ。
それでは式に戻ります。
=\sqrt{\cfrac{1}{n^2}(\sigma^2+\sigma^2+\cdots+\sigma^2)}
=\sqrt{\cfrac{1}{n^2}\cdot n\sigma^2}
=\cfrac{\sigma}{\sqrt{n}}
ということで,標本平均の標準偏差は,母標準偏差を\sqrt{n}で割ったものになります。
 粗茶さん
粗茶さんきっと覚えてしまうことになりますが,\sqrt{n}で割る理由がわからなくなったら,もう一度ここに戻ってきてね…。
母平均 m,母標準偏差 \sigma の母集団から大きさ n の標本を無作為に抽出するとき,標本平均\overline{X}の期待値と標準偏差は,
E(\overline{X})=m,\sigma(\overline{X})=\cfrac{\sigma}{\sqrt{ n}}
標本平均と正規分布
標本平均 \overline{X} の分布については,次の法則が成り立つことが知られています。
母平均 m,母標準偏差 \sigma の母集団から大きさ n の無作為標本を抽出するとき,標本平均\overline{X} は,n が大きいとき,近似的に正規分布 N\left(m,\cfrac{\sigma^2}{n}\right) に従うとみなすことができる。
理由はあまり重要ではないので,とりあえず省略。
正規分布で解けるということを知っておけばOK。
ちょいと例題を。
母平均50,母標準偏差20をもつ母集団から,大きさ100の無作為標本を抽出するとき,その標本平均\overline{X} が54より大きい値をとる確率を求めよ。
正規分布に従うことから,正規分布表で確率を探していけばいいやつです。
m=50,\sigma=20,n=100 だから,この標本平均 \overline{X} は近似的に正規分布N\left(50,\cfrac{20^2}{100}\right),すなわちN(50,4) に従う。
平均50,分散4の正規分布なので,標準偏差は\sqrt{4}=2ですね。
ここで,Z=\cfrac{\overline{X}-平均}{標準偏差} が標準正規分布に従うんでした。
ここで,Z=\cfrac{\overline{X}-50}{2} は,近似的に標準正規分布N(0,1)に従う。
\overline{X}=54 とすると,Z=2 である。
正規分布表で2のところをひくと0.4772と書いてあるので,
P(\overline{X}>54)=P(Z>2)
=0.5-0.4772=0.0228 …(答)
推定
材料が揃ったので,ここからが本番です。
共通テストで出る推定は,母平均の推定と母比率の推定の2つです。
2つといっていますが,そんなに大きく違うわけではありませんけどね。
母平均の推定
母平均がわかっていない母集団から無作為に抽出した標本の標本平均を用いて,母平均を推定します。
もちろん「母平均は165.5cmだ!!!」みたいにピンポイントに当てるのは無理です。
母平均の推定では,「95%の確率で,ここからここの間に母平均がありますよ」のように,区間を求めます。
「●●%の確率で母平均mを含む区間」のことを,「母平均mに対する信頼度●●%の信頼区間」といいます。
 粗茶さん
粗茶さんほとんどの問題は95%の信頼区間を求めさせるので,95%で説明しますね。
先程の「標本平均の分布」のところで,母平均 m,母標準偏差\sigma の母集団から抽出された大きさ nの無作為標本の標本平均 \overline{X} は,n が大きいとき,近似的に正規分布N\left(m,\cfrac{\sigma^2}{n}\right) に従うんでした。
そして,Z=\cfrac{\overline{X}-m}{\cfrac{\sigma}{\sqrt{n}}} は,近似的に正規分布N(0,1) に従います。
正規分布表の値が0.475(0.95の半分)になるとき,z=1.96なので,
P(-1.96\leqq Z\leqq 1.96)=0.95
ということです。これを変形して,mの範囲に直していきます。
-1.96\leqq Z\leqq 1.96
⇔-1.96\leqq \cfrac{\overline{X}-m}{\cfrac{\sigma}{\sqrt{n}}}\leqq 1.96
⇔-1.96\cdot\cfrac{\sigma}{\sqrt{n}}\leqq \overline{X}-m\leqq 1.96\cdot\cfrac{\sigma}{\sqrt{n}}
各辺(-1)倍して,
-1.96\cdot\cfrac{\sigma}{\sqrt{n}}\leqq m-\overline{X}\leqq 1.96\cdot\cfrac{\sigma}{\sqrt{n}}
⇔\overline{X}-1.96\cdot\cfrac{\sigma}{\sqrt{n}}\leqq m\leqq \overline{X}+1.96\cdot\cfrac{\sigma}{\sqrt{n}}
これで m の範囲になりました。つまり,
P\left(\overline{X}-1.96\cdot\cfrac{\sigma}{\sqrt{n}}\leqq m\leqq \overline{X}+1.96\cdot\cfrac{\sigma}{\sqrt{n}}\right)=0.95
したがって,\overline{X}-1.96\cdot\cfrac{\sigma}{\sqrt{n}} 以上 \overline{X}+1.96\cdot\cfrac{\sigma}{\sqrt{n}} 以下の範囲に母平均mがある確率が95%だよ。ということになります。
まさにこの範囲が「母平均mに対する信頼度95%の信頼区間」であり,
\left[\overline{X}-1.96\cdot\cfrac{\sigma}{\sqrt{n}},\overline{X}+1.96\cdot\cfrac{\sigma}{\sqrt{n}}\right] と書きます。
 粗茶さん
粗茶さん一般に「a 以上 b 以下の範囲」のことを[a,b] って書きます。
信頼度が95%以外の問題もたまに出ますが,その場合は1.96のかわりに,別の数字がはいることになります(問題による)。
標本の大きさ n が大きいとき,母平均 m に対する信頼度95%の信頼区間は,
\left[\overline{X}-1.96\cdot\cfrac{\sigma}{\sqrt{n}},\overline{X}+1.96\cdot\cfrac{\sigma}{\sqrt{n}}\right]例題をひとつ。
全国から無作為抽出した2500世帯について,年間の米購入量を調査したところ,平均値85.0kg,標準偏差30.6kgであった。全国の1世帯あたりの平均購入量を,信頼度95%で推定せよ。
母標準偏差がわからない場合は,母標準偏差\sigmaのかわりに標本標準偏差Sを使っても大丈夫です。
 粗茶さん
粗茶さん母平均がわかってないのに,母標準偏差だけわかってるって,そもそもどんな状況やねん…
求める信頼区間は,\left[\overline{X}-1.96\cdot\cfrac{S}{\sqrt{n}},\overline{X}+1.96\cdot\cfrac{S}{\sqrt{n}}\right]
標本平均は \overline{X}=85.0,標本標準偏差は S=30.6,標本の大きさは n=2500 だから,
1.96\cdot\cfrac{S}{\sqrt{n}}=1.96\cdot\cfrac{30.6}{2500}\fallingdotseq 1.2
よって,信頼度95%の信頼区間は,
[85.0-1.2,85.0+1.2]
すなわち [83.8,86.2](単位はkg) …(答)
母比率の推定
母平均のときとあまり変わらないのですが,母比率の推定というのもあります。
例えば,「大量生産した製品の中で,不良品がどのくらい入っているか」のようなことを推定します。
不良品の例でいうと,全製品の中に含まれる不良品の比率を母比率(通常は p で表す),一部を抽出した標本の中の不良品の比率を標本比率(通常はR で表す)といいます。
製品には「不良品」と「不良品でない」の2種類しかないので,大きさ n の標本中の不良品の個数をTとすると,T は二項分布 B(n,p) に従います。
二項分布のときにやりましたが,T の平均は E(T)=np,分散は V(T)=np(1-p) でした。
n が大きいとき,T は近似的に正規分布 N(np,np(1-p)) に従います。
また,標本比率を R とすると,R=\cfrac{T}{n} です。標本の取り出し方によって標本比率も変わるため,R は確率変数で,
E(R)=E\left(\cfrac{T}{n}\right)=\cfrac{1}{n}E(T)=\cfrac{1}{n}\cdot np=p
V(R)=V\left(\cfrac{T}{n}\right)=\cfrac{1}{n^2}V(T)=\cfrac{1}{n^2}\cdot np(1-p)=\cfrac{p(1-p)}{n}
したがって,R は近似的に正規分布 N\left(p,\cfrac{p(1-p)}{n}\right) に従います。
正規分布に従うってことは,信頼区間も求めることができるってことです。
母平均の信頼区間
\left[\overline{X}-1.96\cdot\cfrac{\sigma}{\sqrt{n}},\overline{X}+1.96\cdot\cfrac{\sigma}{\sqrt{n}}\right] の,
標本平均 \overline{X} を標本比率 R に,
標準偏差 \cfrac{\sigma}{\sqrt{n}} を \sqrt{\cfrac{p(1-p)}{n}} に
書き直せばいいので,母比率 p に対する信頼度95%の信頼区間は,
\left[R-1.96\cdot\sqrt{\cfrac{p(1-p)}{n}},R+1.96\cdot\sqrt{\cfrac{p(1-p)}{n}}\right]
さらに,n が十分大きいとき,R は p に近いとみなしてよいので,ルートの中の p を R に置き換えて,
\left[R-1.96\cdot\sqrt{\cfrac{R(1-R)}{n}},R+1.96\cdot\sqrt{\cfrac{R(1-R)}{n}}\right]
これが信頼区間です。
 粗茶さん
粗茶さんpを推定したいっていうのに,式にpが入ってたら元も子もないからね…
標本の大きさ n が大きいとき,標本比率を R とすると,母比率 p に対する信頼度95%の信頼区間は,
\left[R-1.96\cdot\sqrt{\cfrac{R(1-R)}{n}},R+1.96\cdot\sqrt{\cfrac{R(1-R)}{n}}\right]
こちらも例題を1つ。
ある県の高校3年生から無作為に300人を選び,虫歯がある生徒を数えたところ,210人であった。この県の高校3年生の虫歯の保有率 p を,95%の信頼度で推定せよ。
標本比率は R=\cfrac{210}{300}=0.7
n=300 であるから,
1.96\sqrt{\cfrac{R(1-R)}{n}}=1.96\sqrt{\cfrac{0.7\times 0.3}{300}}\fallingdotseq 0.052
よって,虫歯の保有率 p に対する信頼度95%の信頼区間は,
[0.7-0.052,0.7+0.052]
すなわち,[0.648,0.752] …(答)
まとめ
今回は、統計的な推測(標本、母平均の推定、母比率の推定)について説明しました。
推定についてはかなり複雑な式も出てきますが、その式になる理由も併せて理解しておくと、覚える助けになるかと思います。
仮説検定についても記事にまとめましたので,ぜひ読んでみてくださいね。

おすすめ参考書
数Bの確率を扱っている参考書は数少ないですが,おすすめはこちら。
「センター試験」とありますが,共通テストに変わっても使えますぞ。
このブログでは,自分で勉強しているとき,つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や,勉強が楽しくなる文房具も紹介していますので,よろしければご覧ください!




