数Bの確率統計シリーズの第2回です。
前回は,確率変数・期待値・分散をやりましたが,今回は代表的な確率分布の二項分布と正規分布をやります。
そういうことで,今回もゆるく進めてまいります。




粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。
二項分布
二項分布とは,数Aでやった「反復試行の確率」の確率分布のことです。
反復試行の確率と二項分布
反復試行の確率って,覚えていますか?
1回の試行で事象Aの起こる確率をpとする。この試行をn回行う反復試行において,Aがちょうどr回起こる確率は,
_n{\rm C}_rp^r(1-p)^{n-r}このときの事象Aが起こる回数をXとすると,Xの確率分布を二項分布といって,B(n,p)と書きます。
また,このとき「確率変数Xは二項分布B(n,p)に従う」という独特の言い回しがあります。
なんのこっちゃわからないと思いますので,具体的にやってみます。
コインを5回投げて,表の出る回数をXとすると,Xはどんな確率分布に従うかな?
P(X)は,反復試行の確率で計算できるので,二項分布です。
1回の試行で,表が出る確率pは\cfrac{1}{2},試行回数nは5なので,
確率変数Xは,二項分布B\left(5,\cfrac{1}{2}\right)に従う。といいます。
二項分布の期待値と分散
コインを5回投げて,表の出る回数をXとする。Xの期待値・分散・標準偏差を求めよ。
期待値は,X=0,1,2,3,4,5の確率をそれぞれ出して,掛け算して合計すれば出せますが,今後試行回数が100回とかになるとさすがに別の対応を考えないといけません。
そこで,二項分布の場合は,期待値・分散・標準偏差を簡単に求められる公式があります。ステキ。
確率変数Xが二項分布B(n,p)に従うとき,
\begin{array}{l}
E(X)=np,\\\\
V(X)=np(1-p),\\\\
\sigma(X)=\sqrt{np(1-p)}
\end{array}めちゃ簡単!ステキ!
ということで例題2をやっていきたいと思いますが,
期待値はnとpの積なので,
E(X)=5\cdot\cfrac{1}{2}=\cfrac{5}{2}分散は期待値に1-p(事象Aが起きない確率)をかけたもので,
V(X)=5\cdot\cfrac{1}{2}\cdot\cfrac{1}{2}=\cfrac{5}{4}標準偏差は分散のルートなので,
\sigma(X)=\sqrt{\cfrac{5}{4}}=\cfrac{\sqrt{5}}{2}公式の証明は知らなくても問題は解ける(というか証明が難しい)ので,割愛します。覚えましょう。
正規分布
正規分布は,統計や確率の世界でよく使われる分布の一つで,平均値のあたりにデータが多く集まるという,いい感じの分布ぐらいのイメージでOK。
ちなみに式で表すと、
f(x)=\cfrac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}ですが、見なかったことにしましょう…
 学生の方
学生の方書きたかっただけでしょ。
 粗茶さん
粗茶さんスンマセン…
二項分布と正規分布の関係
実は,二項分布の試行回数をとても多くしていくと,正規分布に近づくことが知られています。
二項分布B(n,p)に従う確率変数Xは,nが大きいとき,近似的に正規分布N(np,np(1-p))に従う。
 粗茶さん
粗茶さん二項分布はB(回数,確率)でしたが,正規分布はN(平均,分散)です。
正規分布はこんな感じのグラフで表されます(mは平均値)。
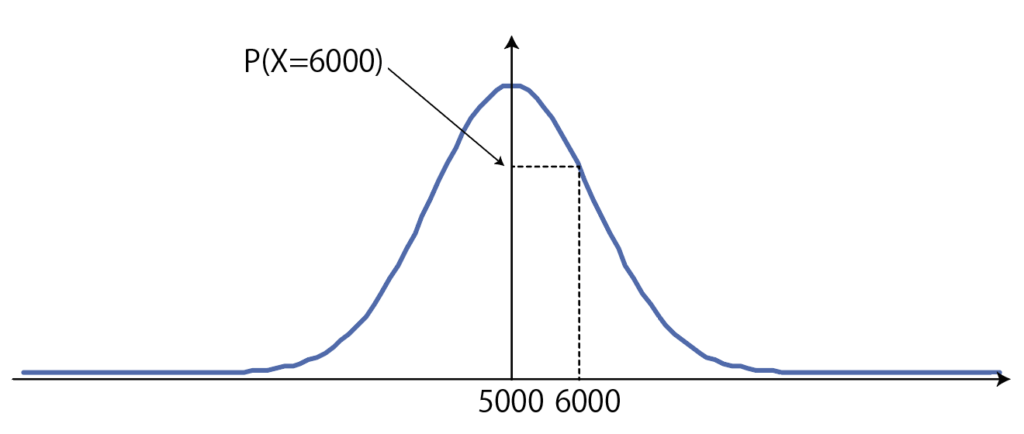
Xがコインを10000回投げて表の出る回数だとすると,Xは二項分布B\left(10000,\cfrac{1}{2}\right)に従うので,
平均は10000\cdot\cfrac{1}{2}=5000,分散は10000\cdot\cfrac{1}{2}\cdot\cfrac{1}{2}=2500です。
試行回数10000は十分大きいので,Xは近似的に正規分布N(5000,2500)に従うってこと。
たとえば,P(X=6000)は,X=6000のときのy座標です。
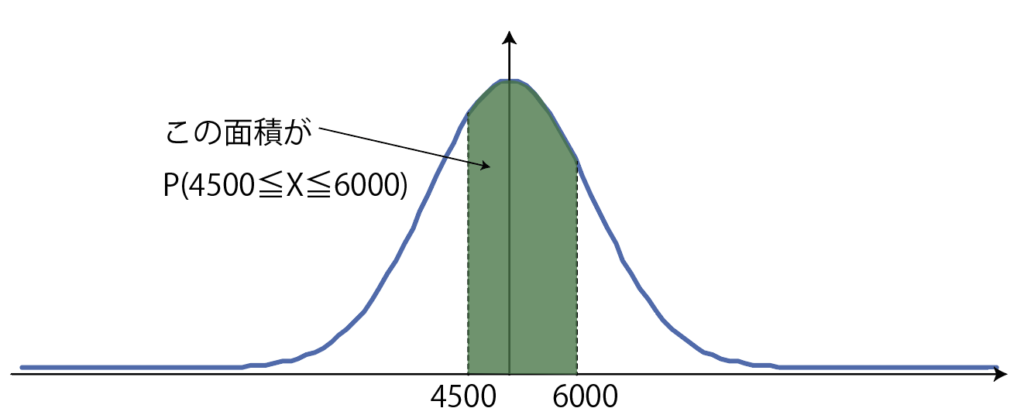
また,P(4500\leqq X\leqq 6000)は,曲線と,X=4500と,X=6000と,X軸で囲まれる面積です。
 学生の方
学生の方y座標とか面積って、どうやって計算するの?
座標や面積は,実際には計算することはなく,次の標準正規分布を用いて求めることができます。
標準正規分布と正規分布表
標準正規分布とは,平均が0,分散が1の正規分布,つまりN(0,1)のことです。
なんと,標準正規分布については,それぞれの値に対応する確率が表にまとめられた正規分布表という神ツールが,問題用紙に載っています。
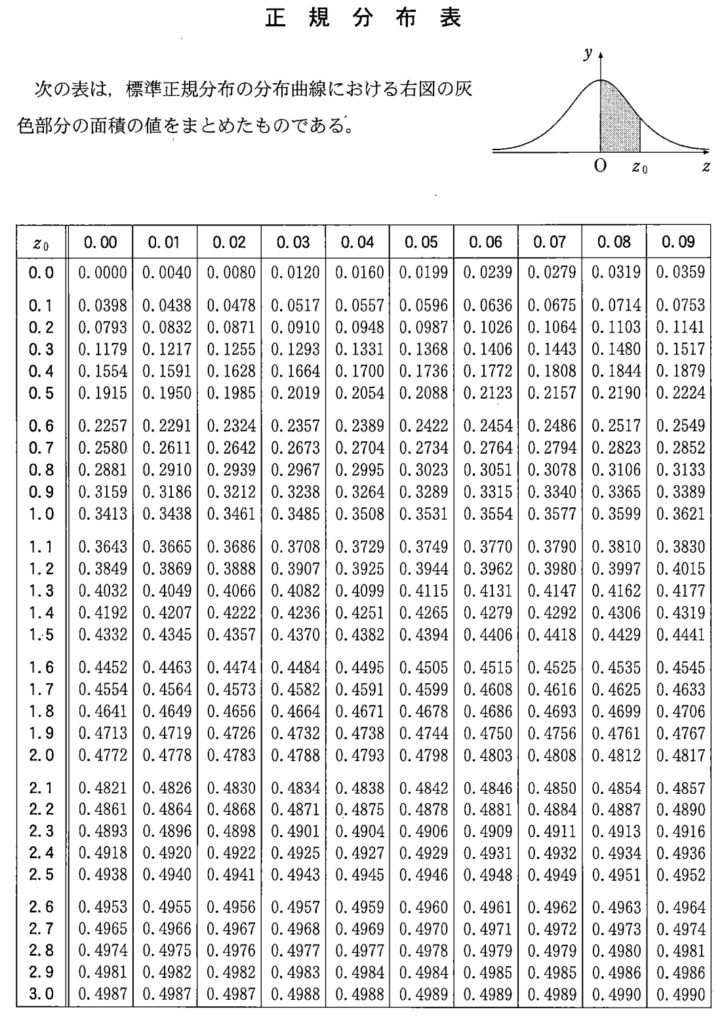
例えば,Xが標準正規分布N(0,1)に従うとき,P(0\leqq X\leqq 1.23)は,下図の面積ですが,
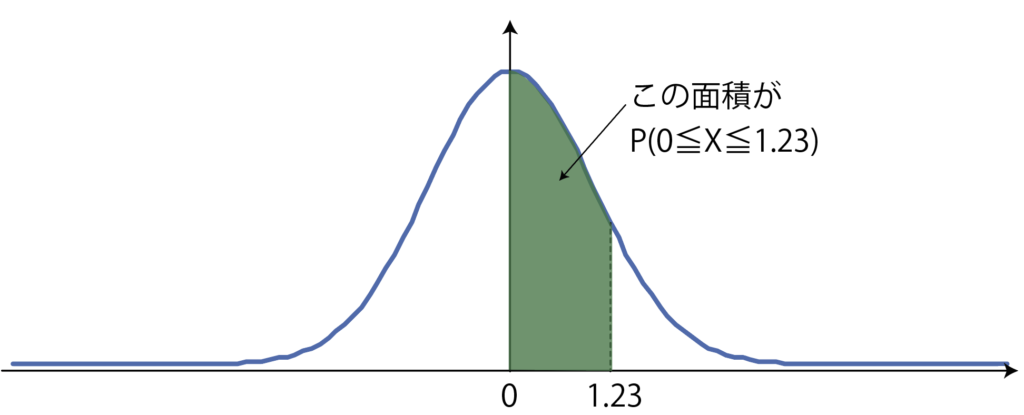
この面積は,正規分布表で1.23のところを探せば,載っています。
上下が小数第1位まで,左右が小数第2位なので,1.23のところには,
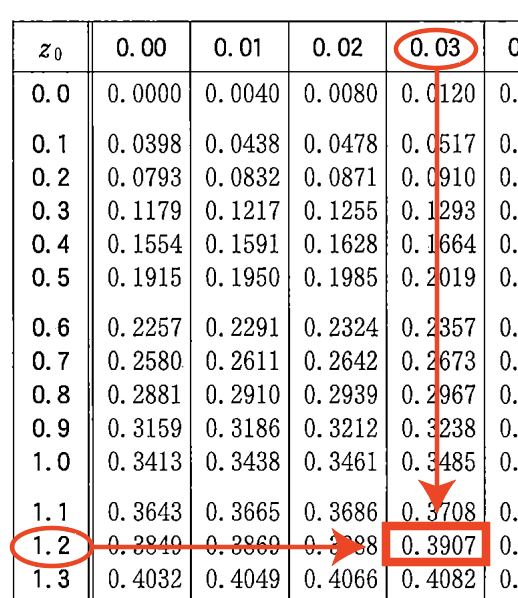
0.3907って書いてあるので,P(0\leqq X\leqq 1.23)=0.3907ということです。
もうひとつ例を。
P(X\geqq 2)と言われたら,下図の面積なのですが,
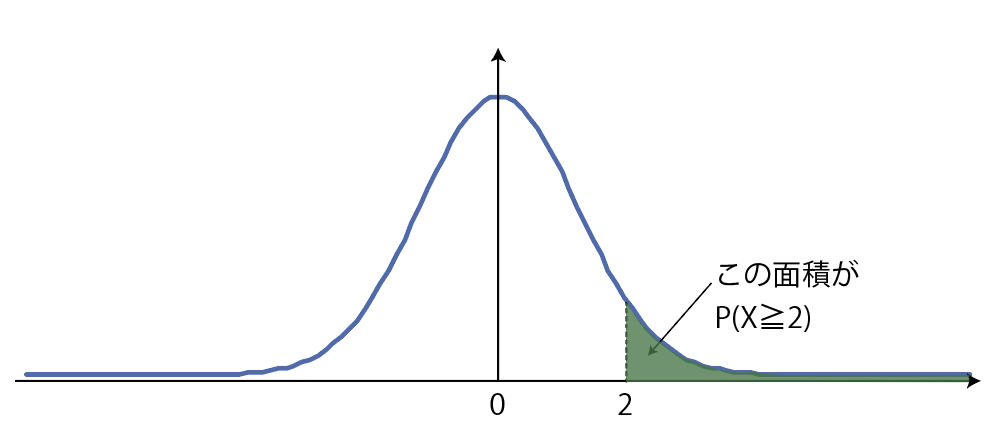
直接出すことができない形なので,工夫します。
全体の半分の面積が0.5なので,0.5から引く形です。
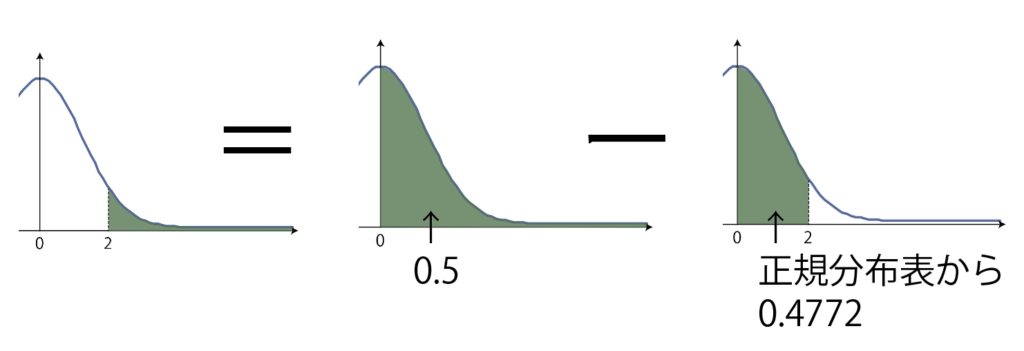
よって,P(X\geqq 2)=0.5-0.4772=0.0228 ってなります。
正規分布と標準正規分布
 学生の方
学生の方標準正規分布のときはいいんだけど,標準じゃない正規分布のときはどうするの?
実際は,最初から標準正規分布に従う確率変数なんて出てきません。
ですが,正規分布に従う確率変数Xについて,次の事実が知られています。
確率変数Xが正規分布N(m,\sigma^2)に従うとき,
Z=\cfrac{X-m}{\sigma}
とおくと,確率変数Zは標準正規分布N(0,1)に従う。
ですので,XをZに書き直してしまえば,正規分布表を用いて確率を求めることができるようになるのです。
たとえばこんな問題がよく出てきます。
サイコロ1個を720回投げて,1が出る回数をXとするとき,130\leqq X \leqq 140となる確率を求めよ。
1が出る確率は\cfrac{1}{6}なので,Xは二項分布B\left(720,\cfrac{1}{6}\right)に従う。
Xの期待値mと標準偏差\sigmaは,
m=720\cdot\cfrac{1}{6}=120, \sigma=\sqrt{720\cdot\cfrac{1}{6}\cdot\cfrac{5}{6}}=10なので,Z=\cfrac{X-m}{\sigma}=\cfrac{X-120}{10}は近似的に標準正規分布N(0,1)に従う。
X=130のとき,\cfrac{130-120}{10}=1,
X=140のとき,\cfrac{140-120}{10}=2 で,正規分布表より
P(0\leqq Z\leqq 1)=0.3413, P(0\leqq Z\leqq 2)=0.4772
なので,求める確率は,
\begin{array}{ll}
&P(130\leqq X\leqq 140)\\\\
=&P(1\leqq Z\leqq 2)\\\\
=&P(0\leqq Z\leqq 2)-P(0\leqq Z\leqq 1)\\\\
=&0.4772-0.3413\\\\
=&0.1359
\end{array}となります。
共通テストで出されるのは,二項分布の試行回数が十分に大きいので,正規分布に近似されるというパターンです。
Z=\cfrac{X-m}{\sigma}に書き直す→正規分布表を探す
という流れをしっかりおさえていきましょう。
二項分布と正規分布 まとめ
今回は二項分布と正規分布について説明しました。
覚えておくことは,
- 反復試行は二項分布B(n,p)
- 二項分布の平均はnp,分散はnp(1-p)
- 二項分布の試行回数が大きいと,正規分布N(m,\sigma^2)に近似される。
- 正規分布に従うXを,Z=\cfrac{X-m}{\sigma}に変換すると,標準正規分布N(0,1)
- 標準正規分布の確率は,正規分布表から探せる
でした。
二項分布から標準正規分布までの流れはお決まりのものなので,何も考えずにできるぐらいに慣れておきましょう。
次回は統計的推測に行きます。

オススメ参考書
数Bの確率を扱っている参考書は数少ないですが,おすすめはこちら。
「センター試験」とありますが,共通テストに変わっても使えますぞ。
このブログでは,自分で勉強しているとき,つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や,勉強が楽しくなる文房具も紹介していますので,よろしければご覧ください!