「位置ベクトル」を学習すると出てくる，「交点の位置ベクトル」の問題。
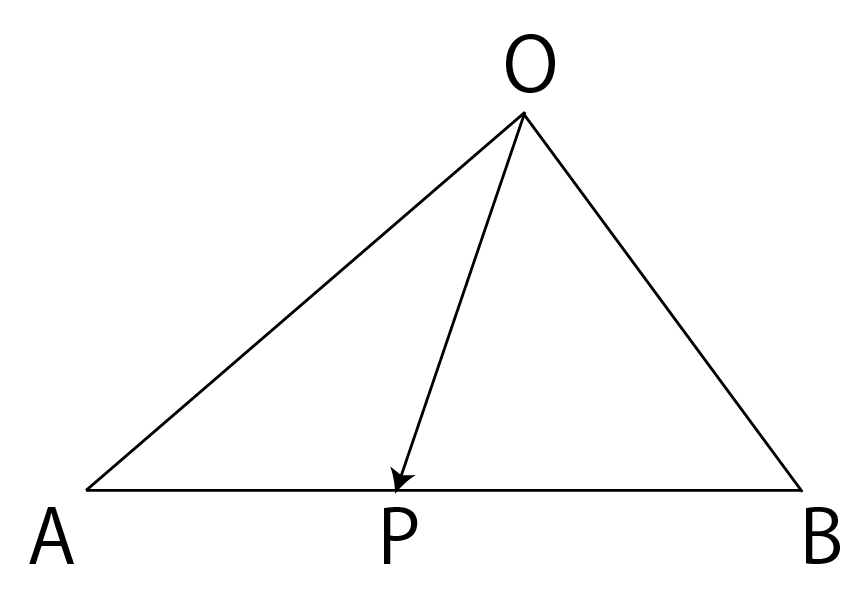
図だとこれです。
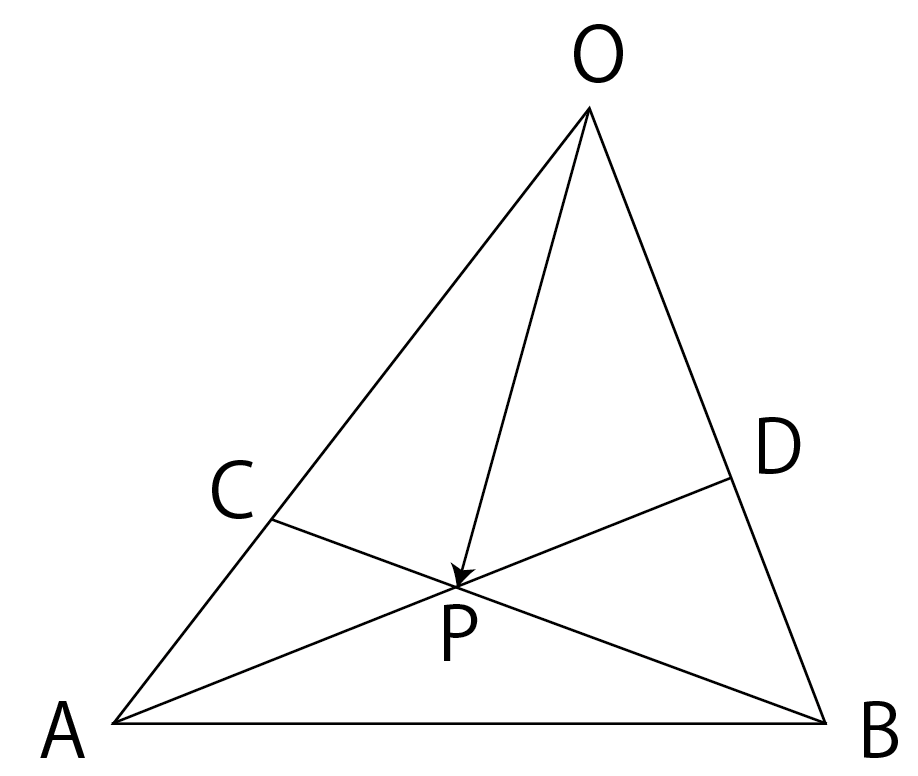
このときの\rm \overrightarrow{OP}を求めよ。っていう問題。
教科書ではsとtをおいて連立方程式を作って解く方法を習いますが，
実は連立方程式を使わずに，交点の位置ベクトルを求める方法があります。
この記事では，交点の位置ベクトルの求め方を３種類紹介します。
お友達が連立方程式をめんどくさそうに解いているのを横目に，自分はスマートな方法でさっさと解いてしまい，優越感を味わいましょう！
- 高校数学・高校公民・中学社会担当の現役塾講師
- 講師歴13年
- 13年の指導経験で知った「生徒がつまづきやすいポイント」や「教科書よりも効率の良い解法」をわかりやすく発信しています。
交点の位置ベクトルの問題の解き方３選
今回扱う問題はこちら。
三角形\rm ABCについて，辺\rm OAを2:1に内分する点を\rm C，辺\rm OBを3:2に内分する点を\rm Dとする。２つの線分\rm ADと\rm BCの交点を\rm Pとするとき，\overrightarrow{\rm OP}を\overrightarrow{\rm OA}と\overrightarrow{\rm OB}で表せ。
図示するとこんな感じ。
わかっている比を利用して，\overrightarrow{\rm OP}を\overrightarrow{\rm OA}と\overrightarrow{\rm OB}で表してね。という問題です。
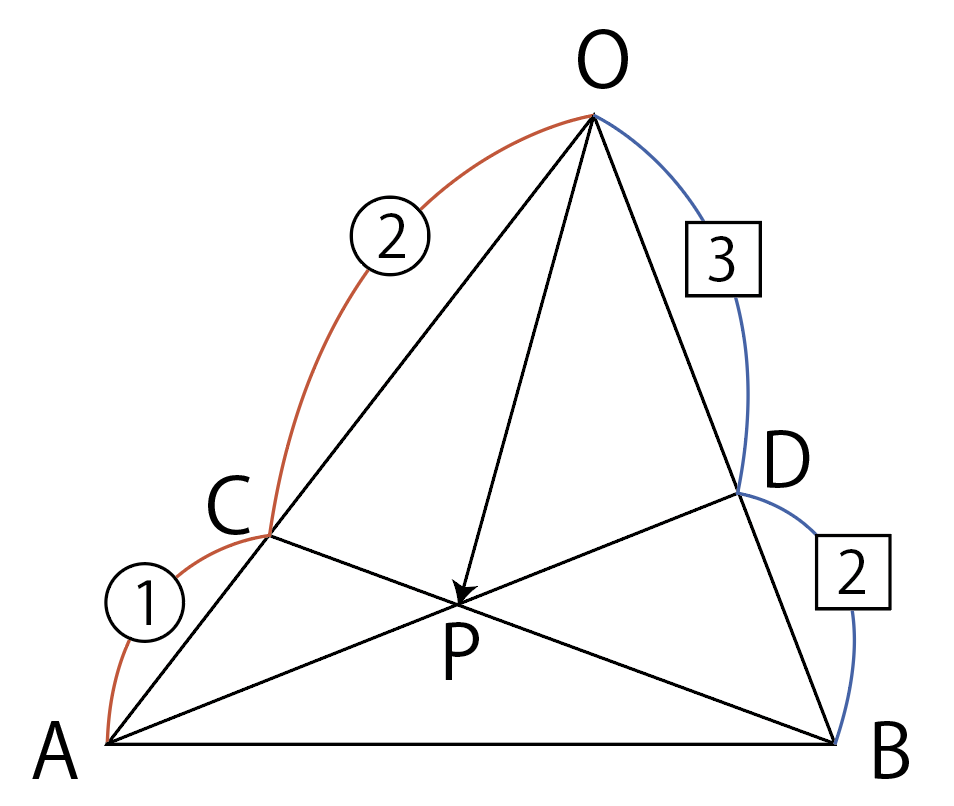
この問題の解き方を3種類紹介します。
- 教科書的方法（連立方程式を解く）
- １つの文字で解く方法
- 文字を使わない方法（メネラウスの定理を使う）
それでは順に紹介していきます。
教科書的な方法（連立方程式）
交点の位置ベクトルの問題，教科書では連立方程式を解く方法が載っています。
\overrightarrow{\rm OP}を，文字を使って2種類の式で表します。
\rm Pは，\rm AD上にあるので，
{\rm AP:PD}=(1-s):sとおけます。
また，\rm Pは，\rm CB上にもあるので，
{\rm CP:PB}=(1-t):tとおけます。
粗茶さん{\rm AP:PD}=(1-s):sじゃなくて，{\rm AP:PD}=s:(1-s)でもOK。tも同様。
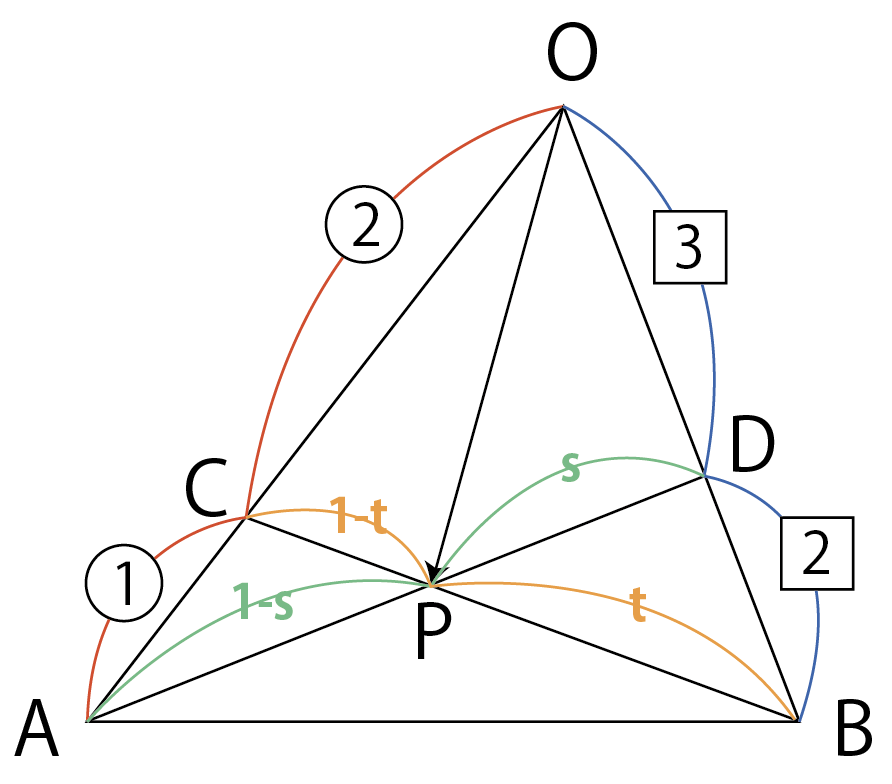
{\rm AP:PD}=(1-s):sより，
\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+(1-s)\overrightarrow{\rm OD}
\therefore \overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+\cfrac{3}{5}(1-s)\overrightarrow{\rm OB} …①
粗茶さん\rm OD:DB=3:2だから，\overrightarrow{\rm OD}=\cfrac{3}{5}\overrightarrow{\rm OB}
また，
{\rm CP:PB}=(1-t):tより，
\overrightarrow{\rm OP}=t\overrightarrow{\rm OC}+(1-t)\overrightarrow{\rm OB}
\therefore \overrightarrow{\rm OP}=\cfrac{2}{3}t\overrightarrow{\rm OA}+(1-t)\overrightarrow{\rm OB} …②
粗茶さん\rm OC:CA=2:1だから，\overrightarrow{\rm OC}=\cfrac{2}{3}\overrightarrow{\rm OA}
①と②は同じベクトル\overrightarrow{\rm OP}を表しています。
同じということは，\overrightarrow{\rm OA}の係数どうしが等しいし，\overrightarrow{\rm OB}の係数どうしも等しくなる。
\overrightarrow{\rm OA}と\overrightarrow{\rm OB}は一次独立なので，各係数を比較して，
s=\cfrac{2}{3}t…③
1-t=\cfrac{3}{5}(1-s)…④
粗茶さん\overrightarrow{\rm OA}と\overrightarrow{\rm OB}が平行でもなければ\overrightarrow{0}でもないことを「\overrightarrow{\rm OA}と\overrightarrow{\rm OB}は一次独立である」といいます。
係数の比較ができるのは，一次独立のときだけ。
③，④を連立させて解きましょう。
③を④に代入して，
1-t=\cfrac{3}{5}\left(1-\cfrac{2}{3}t\right)
⇔ -\cfrac{3}{5}t=-\cfrac{2}{5}
∴ t=\cfrac{2}{3}
③に代入して，
s=\cfrac{2}{3}\cdot\cfrac{2}{3}=\cfrac{4}{9}
sを①に代入して，
\overrightarrow{\rm OP}=\cfrac{4}{9}\overrightarrow{\rm OA}+\cfrac{3}{5}\left(1-\cfrac{4}{9}\right)\overrightarrow{\rm OB}
\therefore \overrightarrow{\rm OP}=\cfrac{4}{9}\overrightarrow{\rm OA}+\cfrac{1}{3}\overrightarrow{\rm OB} …（答）
これで何の問題もないのですが…
学生の方連立方程式めんどくさい。分数の計算やりたくない。
連立方程式になるし，ほぼ間違いなく分母の異なる分数が出てきます。
次は，連立方程式を使わず，文字１つで終わらせる方法を紹介します。
１つの文字で解く方法
交点の位置ベクトルを，１つの文字だけで求める方法です。
連立方程式になる場合は，sとtの2つを使いましたが，今回はsだけをおきます。
（tでもいいです）
\rm Pは，\rm AD上にあるので，
{\rm AP:PD}=(1-s):sとおけます。
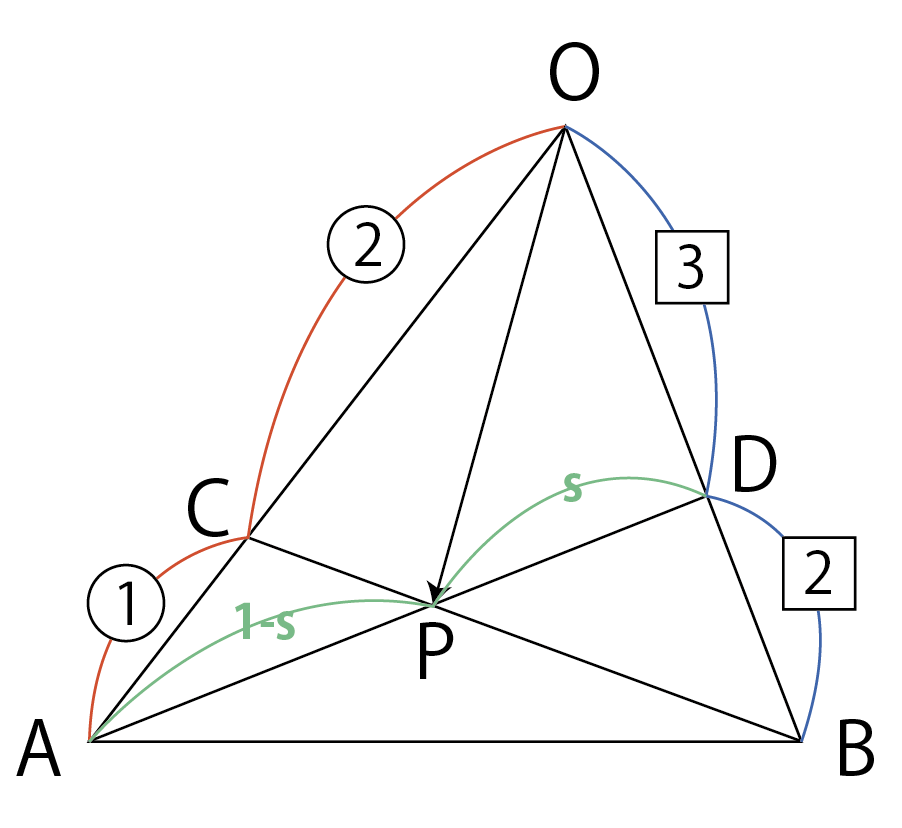
{\rm AP:PD}=(1-s):sより，
\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+(1-s)\overrightarrow{\rm OD} …①
粗茶さんここまでは，tをおいていないだけで，連立方程式のときの同じ流れです。
ここで，点\rm Pは\rm CB上にもあるので，\overrightarrow{\rm OP}を\overrightarrow{\rm OC}と\overrightarrow{\rm OB}で表すことを考えます。
\overrightarrow{\rm OC}=\cfrac{2}{3}\overrightarrow{\rm OA}より，\overrightarrow{\rm OA}=\cfrac{3}{2}\overrightarrow{\rm OC}
\overrightarrow{\rm OD}=\cfrac{3}{5}\overrightarrow{\rm OB}
これらを①に代入して，
\overrightarrow{\rm OP}=\cfrac{3}{2}s\overrightarrow{\rm OC}+\cfrac{3(1-s)}{5}\overrightarrow{\rm OB}
さらにここで，直線上の点に関する超重要なことがあります。
直線{\rm AB}上に点\rm Pがあるとき，
\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}，
s+t=1（係数の和が１）
今回は，点\rm Pが\rm CB上にあるので，
\overrightarrow{\rm OC}の係数\cfrac{3}{2}sと\overrightarrow{\rm OB}の係数\cfrac{3(1-s)}{5}の和が１になります。つまり，
\cfrac{3}{2}s+\cfrac{3(1-s)}{5}=1
⇔15s+6(1-s)=10
∴s=\cfrac{4}{9}
①に代入して計算すると，
\overrightarrow{\rm OP}=\cfrac{4}{9}\overrightarrow{\rm OA}+\cfrac{5}{9}\overrightarrow{\rm OD}
\overrightarrow{\rm OD}=\cfrac{3}{5}\overrightarrow{\rm OB} だったので，
\overrightarrow{\rm OP}=\cfrac{4}{9}\overrightarrow{\rm OA}+\cfrac{5}{9}\cdot\cfrac{3}{5}\overrightarrow{\rm OB}
∴\overrightarrow{\rm OP}=\cfrac{4}{9}\overrightarrow{\rm OA}+\cfrac{1}{3}\overrightarrow{\rm OB} …（答）
粗茶さん「係数の和が１」は，位置ベクトルでは非常に重要なので，使いこなせるようにしておきたい！
文字をおかない方法（メネラウスの定理の利用）
学生の方結局AP：PDが分かればいいんじゃないの？
と思ったアナタは正解です。
AP：PD（またはCP：PB）がわかりさえすれば，\overrightarrow{\rm OP}を求めることができます。
ベクトルを使わない方法として，メネラウスの定理を使うこともできます。
図のように，三角形\rm OADと直線\rm CBがあるとき，
\rm \cfrac{AP}{PD}\cdot\cfrac{DB}{BO}\cdot\cfrac{OC}{CA}=1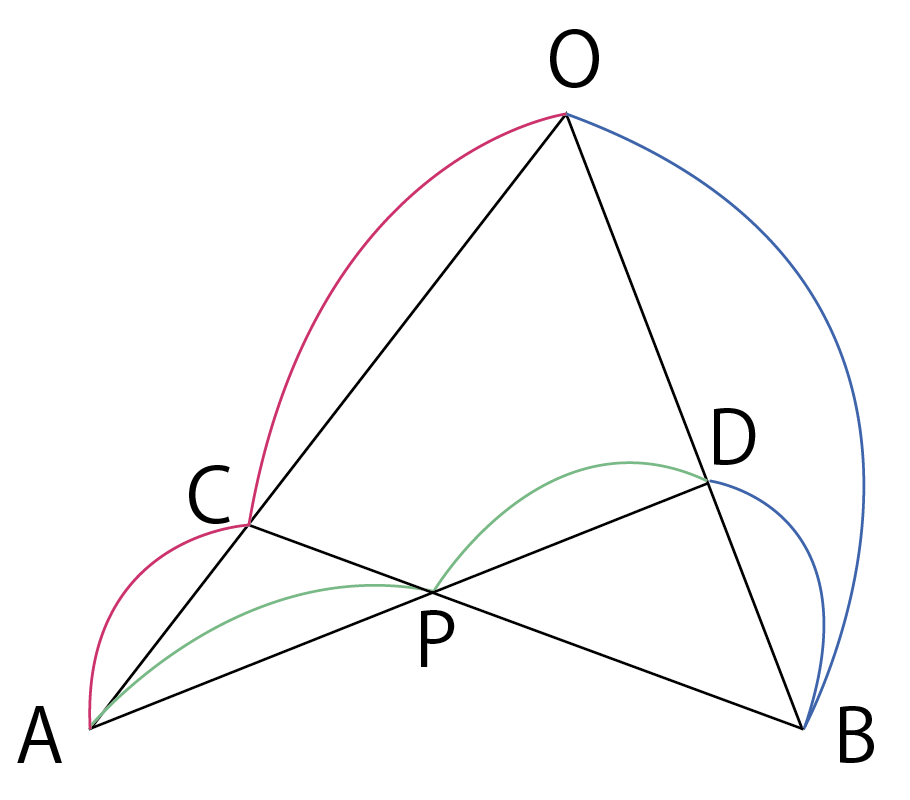
定理の説明は長くなるのでこの記事では省きますが，
メネラウスの定理を使うことで，AP：PDの比を求めることができてしまいます。
ここから解答。
メネラウスの定理より，
\rm \cfrac{AP}{PD}\cdot\cfrac{DB}{BO}\cdot\cfrac{OC}{CA}=1
それぞれの比を代入して，
\rm \cfrac{AP}{PD}\cdot\cfrac{2}{5}\cdot\cfrac{2}{1}=1
∴\rm \cfrac{AP}{PD}=\cdot\cfrac{5}{4}
つまり，\rm AP:PD=5:4
\rm Pは\rm ADを5:4に内分するので，
\rm \overrightarrow{OP}=\cfrac{4}{9}\overrightarrow{OA}+\cfrac{5}{9}\overrightarrow{OD}
\overrightarrow{\rm OD}=\cfrac{3}{5}\overrightarrow{\rm OB} だったので，
\overrightarrow{\rm OP}=\cfrac{4}{9}\overrightarrow{\rm OA}+\cfrac{5}{9}\cdot\cfrac{3}{5}\overrightarrow{\rm OB}
∴\overrightarrow{\rm OP}=\cfrac{4}{9}\overrightarrow{\rm OA}+\cfrac{1}{3}\overrightarrow{\rm OB} …（答）
このようにして，比がわかりさえすればいいので，メネラウスの定理を使う方法も有効です。
というか，けっこうオススメです。
交点の位置ベクトル まとめ
交点の位置ベクトルの求め方を３通り紹介しました。
- 連立方程式でやる（教科書的）
- １つの文字でやる
- メネラウスの定理で比を求める
「AP：PD（または「CP：PB）を求める」という目的はすべて同じです。
基本的には好きな方法でやってもらっていいのですが，
共通テストなどの穴埋め形式の問題の場合は，連立方程式の方法を指定されることがあります。
複数の方法で導けるようにしておきましょう。
このブログでは，自分で勉強しているとき，つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や，勉強が楽しくなる文房具も紹介していますので，よろしければご覧ください！
コメント