 学生の方
学生の方仮説検定を習ったんだけど、有意水準とか棄却域とか、何をしてるのかわかんない。
数Bの確率統計の最後に、仮説検定があります。
仮説検定とは,何かについての仮説が正しいかどうかを,データを使って確認する方法のことです。
- 教科書の例題を真似していれば、なんか問題は解ける。
- でも、何を仮説と置くか、自分でできる自信はない。
- 両側検定と片側検定って使い分けるの?
って、思っていませんか?
この記事では、仮説検定の考え方をわかりやすく説明します。
また、実際の問題での解答の作成方法、両側検定・片側検定の見分け方も紹介しますよ。
それではいってみましょう!
- 仮説検定の考え方がわかる
- 二項分布・正規分布を用いた仮説検定の問題の解き方がわかる
- 両側検定・片側検定の違いがわかる



粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

仮説検定とは
仮説検定とは,何かについての仮説(予想)が正しいかどうかを,データを使って確認する方法です。
具体的な問題で説明します。
その辺にあったコインを30回投げたら表が22回出たんだけど、このコイン、表が出やすくなっているのかなあ?
通常のコインは,表と裏が同じ確率で出るので,1回投げて表が出る確率は1/2=0.5です。
コインを30回投げれば,表は半分の15回ぐらい出そうな気がしますよね。
もちろん毎回ジャスト15回とはならないので、16回とか17回の場合もよく起こりそうです。
これが例えば30回投げて30回とも表だった場合,このコインについてどう思いますか?
 学生の方
学生の方絶対あやしい!表が出やすい細工がしてあるに違いないわ!
表の回数が多すぎるという結果が出た場合、
「普通のコインではめったに起こらないことが起きた。このコイン、表が出やすい加工が施されているぞ!」
と考えられます。
表の回数が29回とか28回とかだった場合も同様に、「このコインは表が出やすくなっている」といえそうです。
では、「30回中22回表が出た」という結果から、「このコインは表が出やすくなっている」と判断していいのでしょうか?
 学生の方
学生の方うーん,22回は…偶然起きたと考えられなくはないかも…??
「30回中22回表」という事象がどのくらい起こりうるのか、「コインを30回投げる」という試行を300回繰り返して調べてみました。
 学生の方
学生の方ほんとに投げたの?
 粗茶さん
粗茶さん実際はコンピューターでシミュレーションしました…
結果が、こちら!!

表が22回以上出たのは、300回中4回(22回が1回、23回が3回)だけでした。その確率は
4\div300=0.0133\cdots
つまり、約1.3%。
こんな、ほぼあり得ないことが起きてしまったということは、このコインが普通のものである(表と裏が等しい確率で出る)という仮説は間違っていて(仮説は棄却されるといいます)、このコインは表が出やすいものであると考えられます。
 学生の方
学生の方でも、「めったに起きない」と感じるかどうかは人によって違うんじゃないの?
実際に問題を解くときには、何%以下だったら仮説を棄却するかという基準(有意水準といいます)をあらかじめ決めておきます。
 粗茶さん
粗茶さん有意水準は何%でもいいんですが、5%か1%の問題が多いです。
有意水準5%の場合,大きすぎる2.5%と,小さすぎる2.5%をあわせて5%。
有意水準1%の場合,大きすぎる0.5%と,小さすぎる0.5%をあわせて1%という意味です。
今回の場合、起こる確率が1.3%だったので、有意水準5%で考えた場合,上位2.5%に収まっているので仮説は棄却され、有意水準1%で考えた場合は上位0.5%に入らないので仮説は棄却されない(表が出やすいコインだとはいえない)ことになります。
仮説が棄却されなかった場合、「仮説が間違っているとはいえない」ことがわかっただけです。仮説が正しいということを示せたことになってはいないので、気をつけましょう。
正規分布を使った仮説検定
 学生の方
学生の方意味はわかったけど,毎回コインを投げ続けるのは無理。
 粗茶さん
粗茶さんさすがに300回も投げることはないです。
テストの問題では,今まで学んだ二項分布や正規分布の知識を使って仮説検定を行います。
二項分布や正規分布については,以下の記事で復習しましょう。


先程と同じような例を用いて,統計の知識で仮説検定をしてみます。
あるコインを 100回投げたら表が65回出た。このコインは表と裏の出方に偏りがあると判断してよいか。有意水準5%で検定せよ。
コインを1回投げて表が出る確率をpとする。
コインの表と裏の出方に偏りがあるならば,p\neq 0.5である。
ここで,「表と裏の出方に偏りはない」,すなわちp=0.5という仮説を立てる。
 粗茶さん
粗茶さん冒頭は,だいたいこんな流れになります。
基本的に「イコール」になるものを仮説とします。
仮説が正しい(コインが普通のやつ)場合,表か裏かの二択なので,表の出る回数は二項分布になります。
コインを100回投げて表の出る回数をXとすると,p=0.5ならば,Xは二項分布B(100,0.5)に従う。
Xの期待値は100\times0.5=50,
Xの分散は100\times0.5\times(1-0.5)=25,
Xの標準偏差は\sqrt{25}=5
試行回数n=100は十分に大きいので、Xは近似的に正規分布N(50,25)に従う。
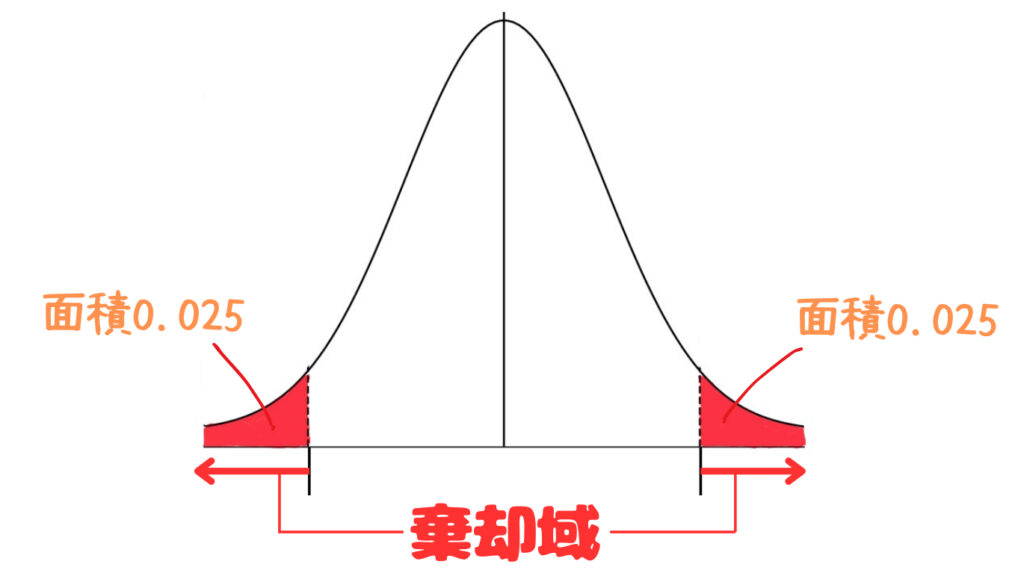
ここでXが65以上の確率P(X\geqq 65)が有意水準5%の半分である2.5%(0.025)以下なら仮説は棄却され,そうでなければ仮説は棄却されない。ということ。
なお,仮説が棄却される範囲のことを棄却域といいます。
有意水準5%の棄却域は下図の部分です。
正規分布に従うXは,標準正規分布に従うZに変換すれば,確率を求めることができましたね。
ここでZ=\cfrac{X-50}{5}とすると,Zは標準正規分布N(0,1)に従うので,
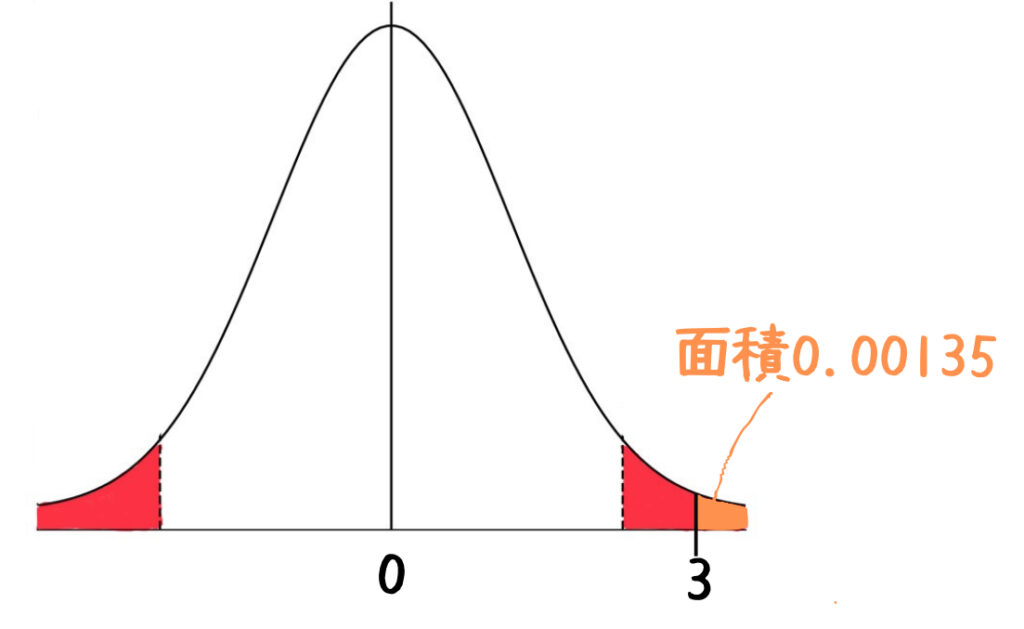
P(X\geqq 65)=P\left(\cfrac{X-50}{5}\geqq \cfrac{65-50}{5}\right)=P(Z\geqq 3)正規分布表で3のところを探すと0.49865になるので,
P(Z\geqq 3)=0.5-0.49865=0.00135
0.00135は0.025よりも小さい。よってZ=3は余裕で棄却域に入ります。
よって,仮説は棄却され,このコインは表と裏の出方に偏りがあると判断してよい。
ということで,やはり65回は多すぎだったんですねえ。
仮説検定の基本的な流れをまとめておきます。
- 事象が起こった状況や原因を推測し,仮説を立てる。
- 有意水準を定め,棄却域を求める。
- 標本から得られた確率変数の値が棄却域に入れば仮説を棄却し,棄却域に入らなければ仮説を棄却しない(仮説が正しいという意味ではない)。
片側検定と両側検定
先ほどのコインの例では、表が出る回数が多すぎても少なすぎても仮説を棄却するので、棄却域をグラフの両端に設定しました。
このように、棄却域を両端(大きい方と小さい方)にとる検定方法を両側検定といいます。
両側検定に対して,棄却域を大きい方or小さい方だけにとる片側検定という方法もあります。
 学生の方
学生の方両側でも片側でも、どっちでやってもいいの?
両側検定でも片側検定でも、やり方は同じですが、問題の問われ方で使い分けます。
- 「〜でないといえるか」「偏っているといえるか」など、仮説より大きすぎても小さすぎても棄却する問題→両側検定
- 「大きい(小さい)といえるか」「増加した(減少した)といえるか」など、大きい(小さい)場合だけを考えればよい問題→片側検定
片側検定の例を1つ。
あるテレビ番組の視聴率は、従来10%であった。無作為に400世帯を調査したところ、50世帯が視聴していることがわかった。視聴率は以前よりも上がったといえるか。有意水準5%で検定せよ。
400世帯中50世帯が観ているとなると、視聴率は12.5%で,従来の10%よりも高いのですが,はたして全体の視聴率も上がったのでしょうか?
調査のときにたまたま観ている人を多く抽出してしまっただけなのか、あるいは実際に全体の視聴率が上がったのかを検定します。
視聴率は上がっていない(10%のまま)という仮説を立てて、この仮説が棄却できるかどうかを調べます。
- 仮説が棄却できる→視聴率は上がったといえる
- 仮説が棄却できない→視聴率は上がったとはいえない(調査した400人の中に,たまたま観ている人が多く含まれていただけ)
と判断します。
現在の視聴率をpとする。
視聴率が上がっているならば、p>0.1である。
ここで、「視聴率は上がっていない」つまりp=0.1と仮定する。
 粗茶さん
粗茶さん各世帯ごとに「観ている」「観ていない」の二択なので、二項分布に従います。
仮説が正しいとすれば、視聴している世帯数Xは、二項分布B(400,0.1)に従い、
Xの期待値は400\cdot 0.1=40,
Xの分散は400\cdot 0.1\cdot 0.9=36
Xの標準偏差は\sqrt{36}=6
世帯数400は十分に大きいので、Xは近似的に正規分布N(40,36)に従う。
さらに,Z=\cfrac{X-40}{6}とすると,Zは標準正規分布N(0,1)に従うので,
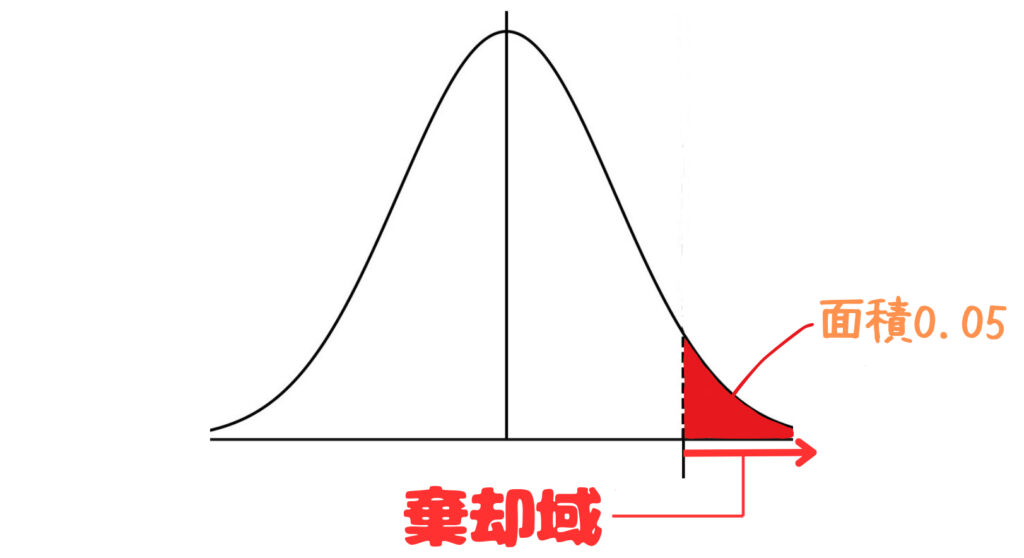
P(X\geqq 50)=P\left(\cfrac{X-40}{6}\geqq \cfrac{50-40}{6}\right)=P\left(Z\geqq \cfrac{5}{3}\right)今回は「上がったといえるか」という問題で、片側検定なので、棄却域は上から5%の部分になります。
正規分布表で\cfrac{5}{3}\fallingdotseq 1.67のところを探すと0.4525になるので、
P\left(Z\geqq \cfrac{5}{3}\right)\fallingdotseq P(Z\geqq 1.67)=0.5-0.4525=0.0475で、ギリギリ棄却域に入ります。
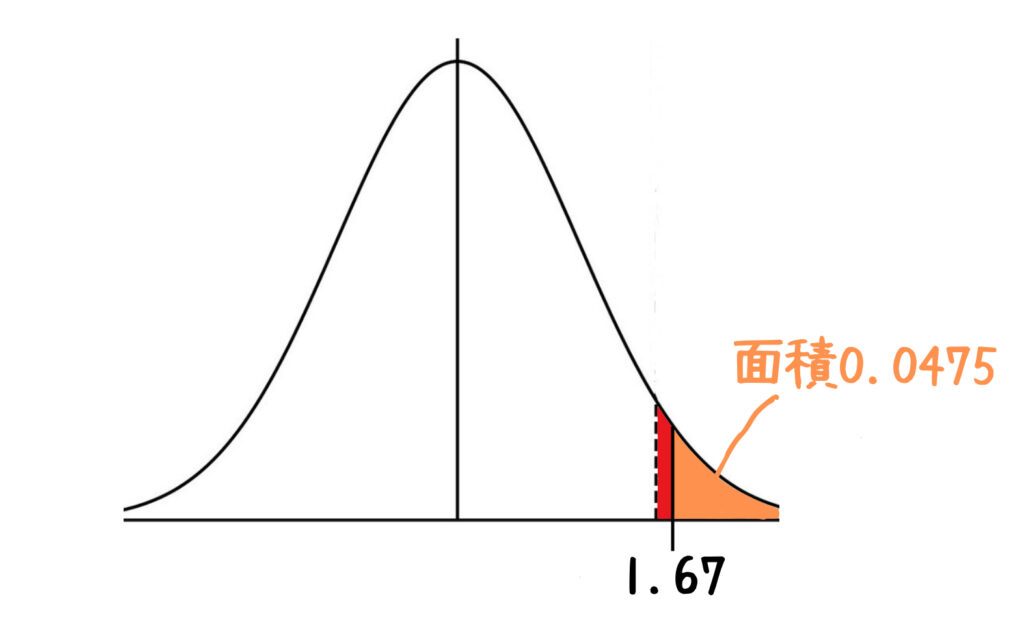
よって、仮説は棄却され、視聴率上がったと考えられる。
この問題、両側検定だったら棄却域の面積が0.025なので、棄却されません。
片側検定は、両側検定よりも棄却される可能性が高いことがわかります。
棄却されやすいということは、「視聴率が上がったといえる」のような判断が実は間違っていた!という可能性も上がることになるので、実用上は慎重に使う必要がありそうです。
 粗茶さん
粗茶さんテストの問題を解く上では、あまり気にしなくてもいいけどね。
まとめ
この記事では、数Bの確率統計の中から、仮説検定のお話をしました。
仮説検定の流れをおさらいすると、
- 事象が起こった状況や原因を推測し,仮説を立てる。
- 有意水準を定め,棄却域を求める(両側検定or片側検定も決める)。
- 標本から得られた確率変数の値が棄却域に入れば仮説を棄却し,棄却域に入らなければ仮説を棄却しない(正しいといえるわけではない)。
でした。確率変数の値が棄却域に入るかどうかは、二項分布の正規分布による近似を用いて求めていきましょう。
仮説検定は流れが決まっているので、流れに沿ってしっかりと解答を作っていきましょう。
大学の授業でもやるでー。
このブログでは,自分で勉強しているとき,つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や,勉強が楽しくなる文房具も紹介していますので,よろしければご覧ください!



