 学生の方
学生の方政経で「信用創造」を習ったんだけど、どういうこと?お金が増えるの?意味わかんないんだけど!
誰かが銀行に預けたお金を銀行が誰かに貸して、そのお金が使われて、そのお金が預金されて、また貸し出されて…を繰り返すことで、実際に存在する現金よりも多くの預金通貨を生み出すことができるしくみを信用創造といいます。
この記事では、銀行による信用創造のしくみを、具体例を交えてわかりやすく説明するとともに、入試の計算で役立つ公式とその使い方を紹介します。
- 信用創造によって預金通貨が増える仕組みがわかる
- 入試で問われる信用創造の計算問題の解き方がわかる

- 高校数学・高校公民・中学社会担当の現役塾講師
- 講師歴13年
- 13年の指導経験で知った「生徒がつまづきやすいポイント」や「教科書よりも効率の良い解法」をわかりやすく発信しています。
信用創造で預金が増える仕組み
銀行が預金と貸付を繰り返すことで、実際に存在する現金の何倍もの預金通貨を作り出すことができるしくみを信用創造といいます。
これだけ書かれてもなんのこっちゃわかんないと思いますので、具体例をあげながら説明してみます。
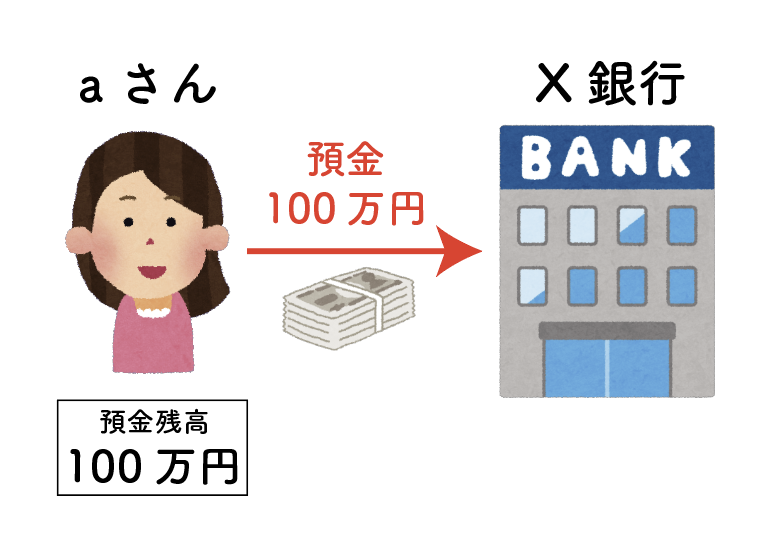
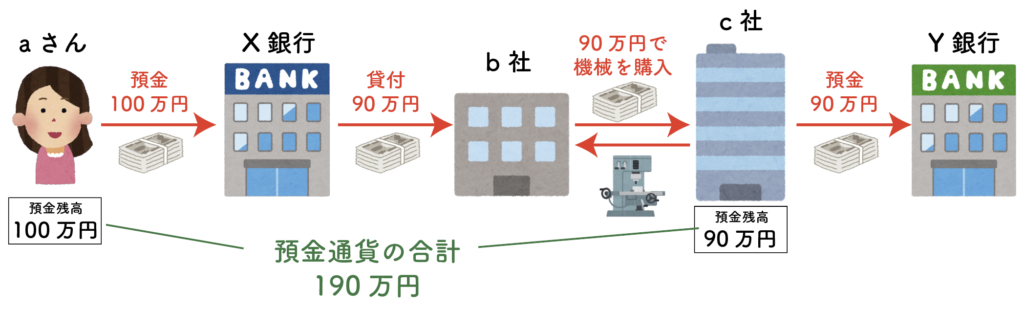
X銀行に口座を持っているaさんが,100万円を預金したとしましょう。
もちろんaさんの預金残高は100万円になります。
ちなみに,最初に預けられたお金を本源的預金といいます。
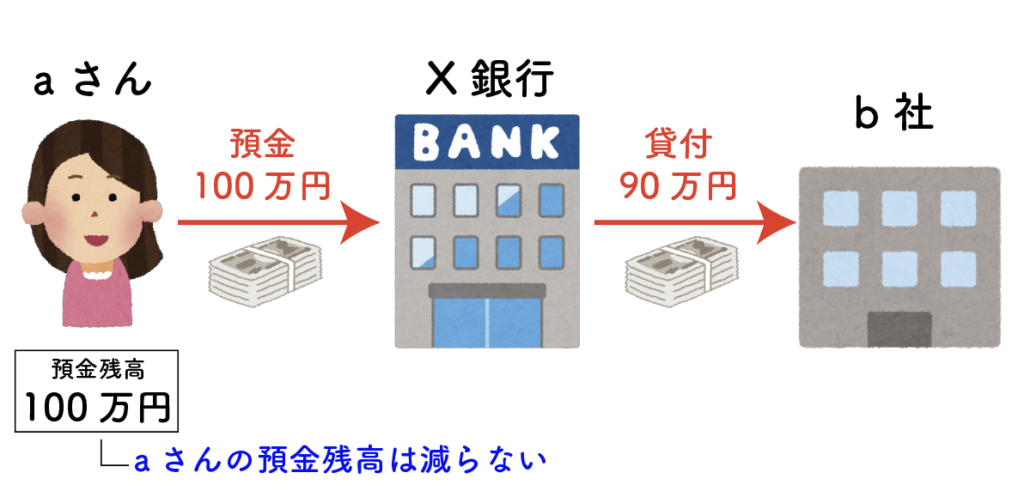
次に、X銀行がこの預金をb社に貸し出しました。ただし、全額を貸し出すと預金の引き出しに対応できなくなるので、10%は貸し出さず、残りの90万円を貸し出しました。
 粗茶さん
粗茶さんこの「貸し出さないで残しておくお金」を支払準備金といい、「残しておく割合」を支払準備率といいます。この例では、支払準備率10%で話を進めます。
aさんが預けたお金はb社に貸し出されていますが、aさんがそれを知ることはなく、aさんの預金額が減ることもないので、aさんの預金残高は100万円のまま。
その後、b社は借りた90万円で、c社から新しい機械を購入しました。
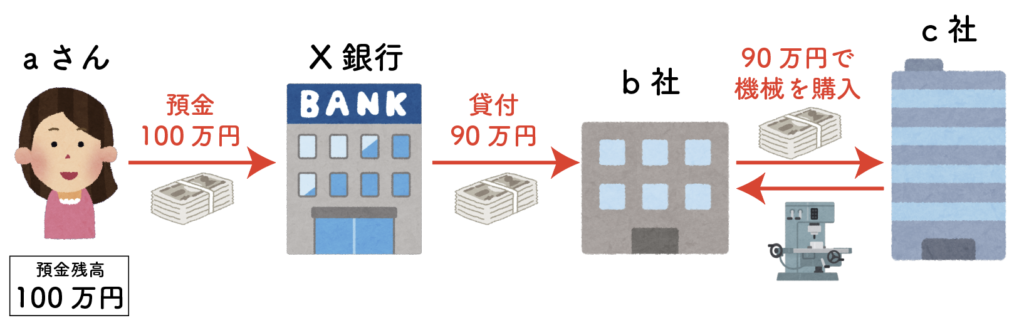
c社には機械の購入代金90万円が入りますが、現金で持ってても仕方がないので、Y銀行に預けました。
すると、c社の預金残高は90万円になります。
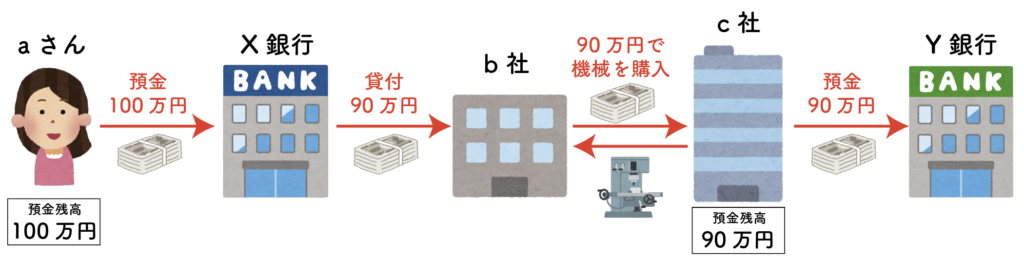
ここで状況を整理しましょう。
aさんが100万円をX銀行に預け、そのうち90万円がb社に貸し出され、その90万円はc社を通じてY銀行に預金されました。
現金はX銀行にある10万円と、Y銀行にある90万円の計100万円であり、全く増えていません。
ですが預金額はどうでしょうか?
aさんはX銀行に100万円を預けたので、aさんの口座残高は100万円。c社はY銀行に90万円を預けたので,c社の口座残高は90万円。両者を足すと預金通貨の合計は190万円で、現金通貨よりも預金通貨がかなり多くなっています。
aさんの100万円も、c社の90万円も、ちゃんとした通貨なので、それぞれ好きな時に使うことができます。
ただし,aさんとc社が同時に全額を出金しないという前提はありますけどね。
このあと,Y銀行が別の人にお金を貸して、そのお金が別の口座に入金されると,さらに預金通貨が増えていきます。
このような信用創造のしくみのおかげで、現金として存在するよりもかなり大きいお金を動かすことができるようになり、国全体の経済活動を活発にすることができるのです。
 学生の方
学生の方ってことは無限にお金が増えるってこと?錬金術?
あくまでも預金が増えているのは、銀行がお金を貸している間だけであって、借金が返済されたり、預金が下ろされたりすれば、その分預金残高が減るので、信用創造は終了になります。
あと、支払準備率があるので、預金の増え方は徐々に小さくなっていき、無限に預金が増え続けるということはありません。
信用創造の計算問題を攻略
信用創造に関する計算問題をやってみましょう。
2019年度大学入試センター試験,政治・経済の問題をもとに作成しました。
次の表のように,銀行Aが2,000万円の預金(本源的預金)を受け入れ,支払準備率10%として企業に貸し出すとする。この貸出金は,企業の取引の支払いに充てられ,支払いを受け取った別の企業によって銀行Bに全額,預金されるとする。銀行Bはこの預金をもとに企業への貸し出しを行い,同様の過程を経て,銀行Cに預金がなされる。この過程が次々と繰り返された場合,信用創造で作り出された銀行全体の預金の増加額はいくらか。
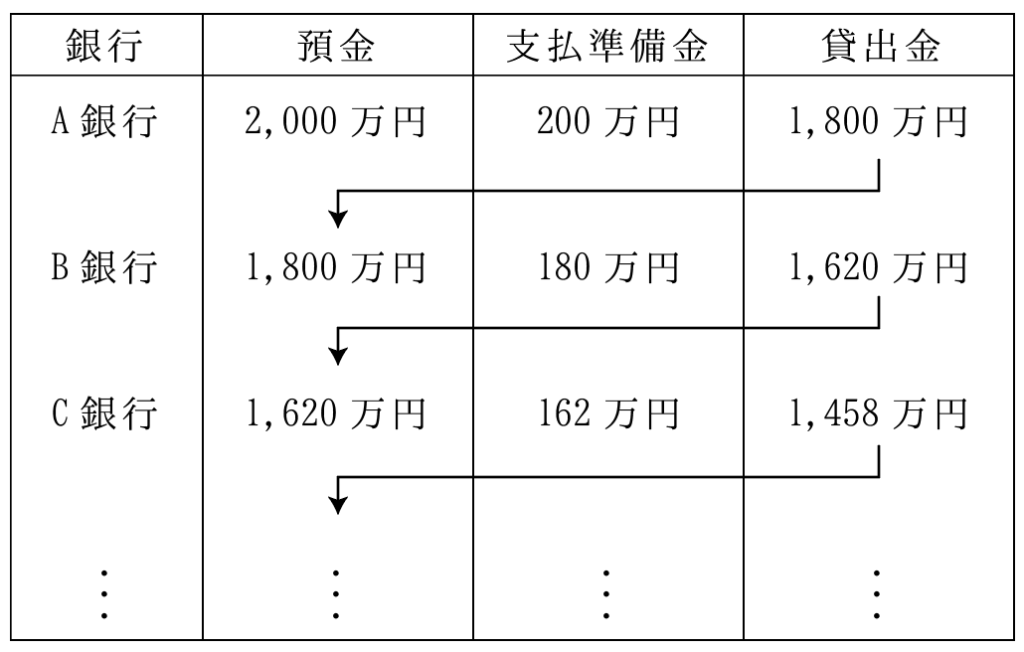
入試で出る形式は決まっていて,銀行が貸付を繰り返した結果,新たに創造された預金額の合計を問う問題がほとんどです。というか,それ以外見たことがない。
信用創造の計算公式
 学生の方
学生の方無限に続いてるのに,計算するとか,無理じゃね?
実は,表の左の列にある預金の合計を求める公式が存在します。
預金の合計=本源的預金÷支払準備率
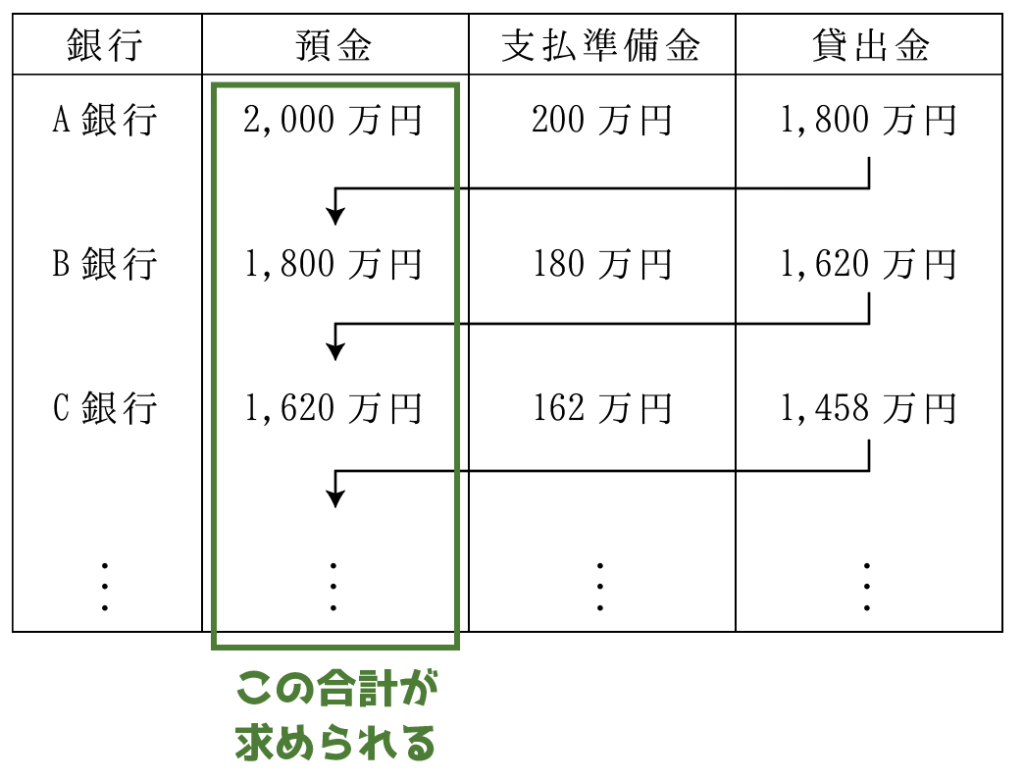
今回は,本源的預金が2000万円,支払準備率は10%(0.1)なので,預金の合計額は,
2000万÷0.1=2億円
ということになります。
ですが,ここで問題をよーく読みましょう。
問題では,信用創造によって増加した預金額を聞いているので,求めるのは,B銀行以下の預金額の合計ということになります。
 粗茶さん
粗茶さん本源的預金は貸出を行う前から存在しているお金なので,増加した金額に入れちゃダメですね。
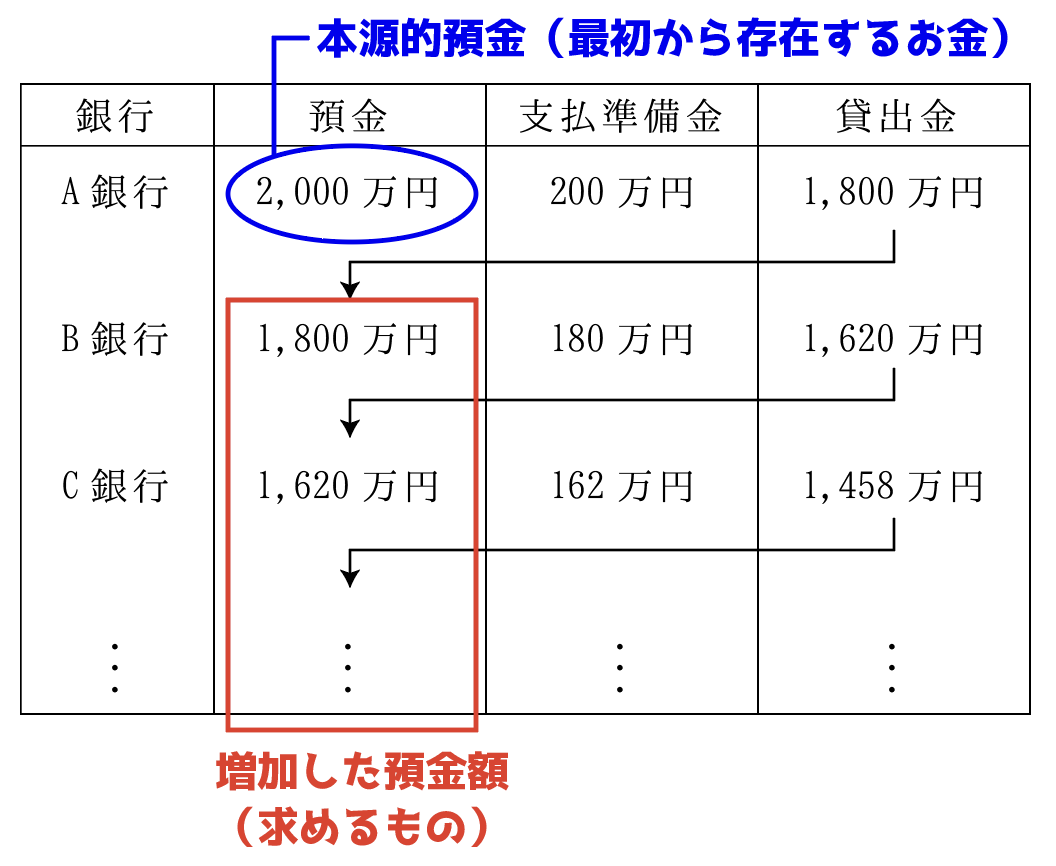
よって答えは,上の式で求めた2億円から,本源的預金2,000万円を引くので,
2億ー2000万=1億8000万円
になります。
信用創造の計算公式が成り立つ理由
 学生の方
学生の方どうして支払準備率で割ると合計が出るの?
 粗茶さん
粗茶さんそんな気になるあなたのために,ご説明差し上げましょう。
ただ,数学(等比数列)の知識が必要なので,苦手な人は飛ばしてね。
預金額に注目します。
支払準備金として10%は残されるので,次の銀行の預金額は,前の銀行の預金額の90%,つまり0.9倍になっています。
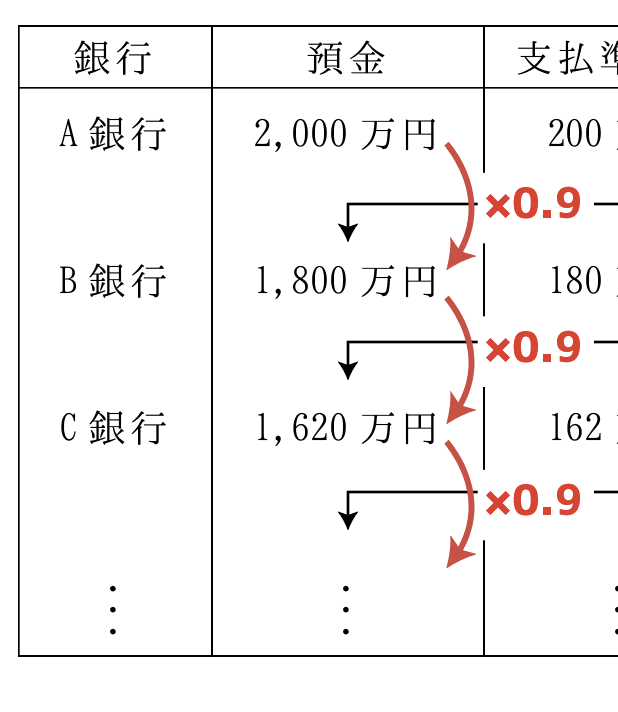
これは初項2000万,公比0.9の等比数列にほかなりません。
つまり預金額の合計は,初項2000万,公比0.9の等比数列の和ということです。
等比数列の和の公式はこちら。
初項a,公比r,項数nの等比数列の和は,
\cfrac{a(1-r^n)}{1-r}今回はa=2000万,r=0.9,項数は無限ですが,とりあえずnとすると,
\cfrac{2000万(1-0.9^n)}{1-0.9}って書けます。分母は計算できて,
\cfrac{2000万(1-0.9^n)}{0.1}分母が預金準備率の0.1になりました。これで「預金準備率で割る」ということは示せました。
問題は分子の0.9^nなんですが,今回は「貸出を次々と行う」ので,nは1とか2とかいう小さい数ではなく,かなり大きな数になります。
例えばn=50とすると,
0.9^{50}=0.005153775で,0に近い値になります。nをもっと大きくすると,0.9^nはもっと小さくなるので,無視できる数になります。
ということで,nがじゅうぶんに大きいとき,求める預金額の合計は,
\cfrac{2000万}{0.1}で計算できるというわけなんですね。
 粗茶さん
粗茶さん公式で求めることができる理由を問われることはないので,数列がよくわからない人は,結果を覚えてしまえばOK!
正しく活用できることが大切!
信用創造の問題は,計算方法だけ覚えれば簡単
ということで,今回は,銀行の信用創造で預金通貨が増える仕組みと,計算問題の攻略法を解説しました。
預金の合計=本源的預金÷支払準備率
をしっかり覚えておきましょう。
また,預金の増加額を答える場合には,預金の合計から本源的預金を引くことも忘れないようにしましょう。
共通テストで毎年出題されるというわけではありませんが,簡単な計算で答えが出せるところなので,得点源にしたいですね!
政治経済 おすすめ参考書
はじめて学習する人にもとっつきやすい一冊。
全編カラーでポップなデザインなので,楽しく読み進められます。
高校生が登下校の電車の中で読んでいるのも時々見かけます。
外で取り出しても平気なデザインっていうのも,結構大事ですよね。
内容のわかりやすさは申し分なし!
このブログでは,自分で勉強しているとき,つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や,勉強が楽しくなる文房具も紹介していますので,よろしければご覧ください!






コメント