学生の方常用対数を使って桁数を求める問題を習ったんだけど、なんか不等式がでてきてわかりづらいんですけど。
粗茶さん不等式…あ、これね。
整数Aがn桁のとき、
n-1\leqq\log_{10}A < nこれは正しいことを言っているのですが、答えが右辺だったか左辺だったかで、いつも迷っていませんか？
実は、桁数の問題は不等式を使わなくても答えを出すことができます。
この記事では、常用対数を使った桁数の問題を、桁数が求められる仕組みも理解できる方法で、わかりやすく解説します。
さらに桁数を求める過程で、ついでに最高位の数までわかってしまうというお得な方法です！
粗茶さんもちろん「小数第何位に初めて0でない数が現れるか」の方もやります。
- 常用対数を用いて、大きな数の桁数と、小さい数の「小数第何位に初めて0でない数が現れるか」を求める方法がわかる
- ついでに、最高位の数と、「初めて現れる0でない数が何か」もわかる
- 高校数学・高校公民・中学社会担当の現役塾講師
- 講師歴13年
- 13年の指導経験で知った「生徒がつまづきやすいポイント」や「教科書よりも効率の良い解法」をわかりやすく発信しています。
常用対数とは
はじめに、常用対数について軽く説明しておきます。
常用対数は底が10の対数
常用対数とは、10を底とする対数、つまり\log_{10}のことです。
ある数Nに\log_{10}をつけて\log_{10}Nにすることを、常用対数をとるといいます。
常用対数をとると「10の何乗か」がわかる
そもそも\log_{a}b=cとは、「bはaのc乗」という意味でした。
このaが10になって、
\log_{10}b=cだったら、「bは10のc乗」という意味になります。
常用対数をとると、ある数が10の何乗であるかがわかるのです。
これを利用して、大きい数の桁数を求めることができます。
常用対数で桁数を求める
常用対数を使って、大きい数の桁数を求めてみましょう。
6^{40}の桁数を求めよ。また、最高位の数字も求めよ。
ただし，\log_{10}2=0.3010，\log_{10}3=0.4771とする。
まずは常用対数をとる
桁数の問題を扱うときは、まず常用対数をとります。
\log_{10}2と\log_{10}3の近似値が出ているので、これらで表すことを考えましょう。
\begin{array}{l}
\log_{10}6^{40}\\\\
=40\log_{10}6\\\\
=40\log_{10}(2\times 3)\\\\
=40(\log_{10}2+\log_{10}3)\\\\
=40(0.3010+0.4771)\\\\
=40\times 0.7781\\\\
=31.124
\end{array}つまり，
\log_{10}6^{40}=31.124ということになります。
対数から指数の形に直して、小数点を動かす
このあと、よくある解答では、
31\leqq\log_{10}6^{40}<\color{red}32よって6^{40}は32桁。
って終わっていることが多いと思います。
これはこれであっているし、公式のように覚えてしまってもいいのですが、
学生の方31桁なのか32桁なのか、いつもわかんなくなっちゃうんだよね…。
答えが不等式の右辺か左辺かどっちかで迷ってしまうことがありそうです。
そこで今回は、不等式を導入せずに答えを求める方法を伝授しますよ。
まずは、対数の定義を思い出しましょう。
指数と対数は書き換えができるんでした。
\large{{\color{red}a}^{\color{blue}b}={\color{green}c}\Leftrightarrow \log_{\color{red}a}{\color{green}c}={\color{blue}b}}つまり\log_{\color{red}10}{\color{green}6^{40}}=\color{blue}31.124ということは、
{\color{green}6^{40}}={\color{red}10}^{\color{blue}31.124}ということになります。
さらに計算を進めていきます。
\begin{array}{ll}
6^{40}\\\\=10^{31.124}\\\\
=10^{0.124}\times 10^{31}
\end{array}31.124を小数部分と整数部分に分けました。
実はここで、10^{0.124}がどのくらいの値なのかは知ることができます。
まず、どんな数も0乗は1なので、
10^0=1
ですね。
次に、問題文にある\log_{10}2=0.3010を指数の形に書き直すと、
10^{0.3010}=2という意味です。
いま求めようとしている10^{0.124}は、1と2の間なので、10^{0.124}は「1.△△△…」いうことがわかります。
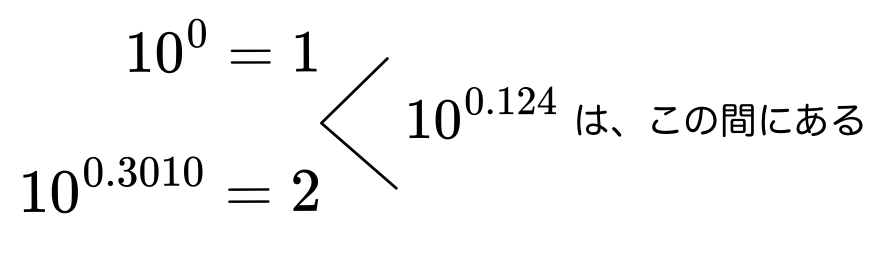
そして、この1.△△△…に10^{31}をかけると6^{40}になるというわけ。
10^{31}をかけるということは、10を31回かける、つまり小数点を右に31回動かすということです。
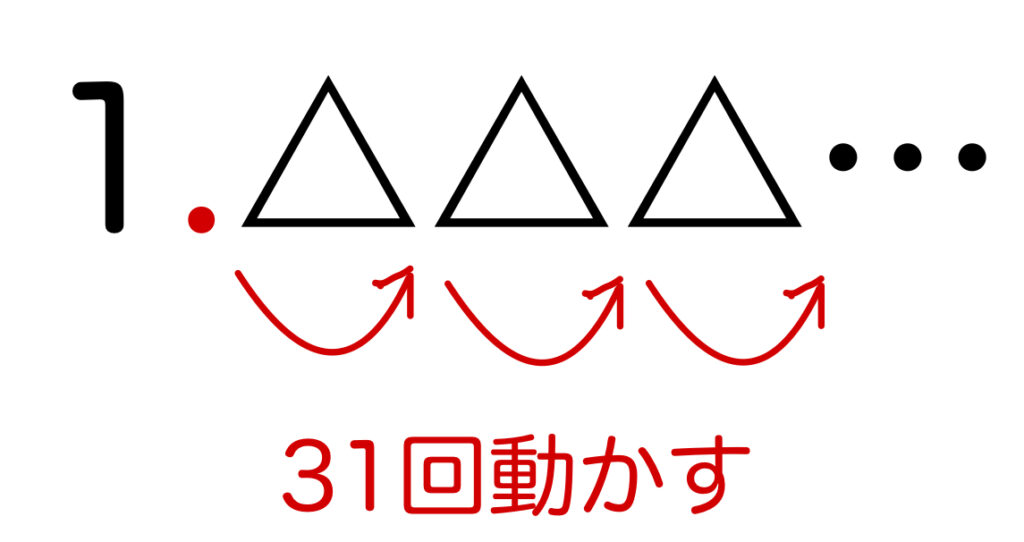
- 小数点を1回動かすと、1△.△△…なので、整数部分は2桁
- 小数点を2回動かすと、1△△.△…なので、整数部分は3桁
同様に続けていって…
小数点を右に31回動かすと、答えは32桁。
1.△△△…の小数点を動かしたので、最高位の数字は1ということもわかっちゃいます。
今回紹介した方法は、桁数がわかるだけでなく、同時に最高位の数字までわかってしまうので、超お得なんですねえ。
常用対数で「小数第何位に初めて0でない数が現れるか」を求める
常用対数を使うと、とても小さい数の小数第何位に初めて0でない数が現れるかを求めることもできます。
学生の方「小数第何位に初めて0でない数が現れるか」って長すぎるんだけど、もっと短くならないの？
粗茶さん「小数首位」って書いてあるのを見たことはあるけど、現状「小数第何位に初めて0でない数が現れるか」が多数派なので…
\left(\cfrac{1}{2}\right)^{100}は小数第何位に初めて0でない数が現れるか求めよ。また、初めて現れる0でない数は何か。
ただし，\log_{10}2=0.3010，\log_{10}3=0.4771とする。
常用対数をとる
取り組み方は例題1と同じで、まずは常用対数をとります。
\begin{array}{l}
\log_{10}\left(\cfrac{1}{2}\right)^{100}\\\\
=100\log_{10}\cfrac{1}{2}\\\\
=100\left(\log_{10}1-\log_{10}2\right)\\\\
=100(0-0.3010)\\\\
=100\times(-0.3010)\\\\
=-30.1
\end{array}対数から指数の形に直して、小数点を動かす
よくある解答では、やはり不等式で挟んで、
-{\color{red}31}< \log_{10}\left(\cfrac{1}{2}\right)^{100}\leqq -30よって\left(\cfrac{1}{2}\right)^{100}は小数第31位に初めて0でない数が現れる。
と終わっているんですが、
学生の方桁数のときは不等式の右辺の数字が答えだったけど、今回は左辺の数が答えになるのか…。
粗茶さん不等式で挟む方法だと、桁数の時と小数第何位の時を別々に覚えなきゃいけないので大変です。
やはり今回も不等式を使わない方法で解いていきます。
例題1と同じように、\log_{10}\left(\cfrac{1}{2}\right)^{100}=-30.1を指数の形に直して、
\left(\cfrac{1}{2}\right)^{100}=10^{-30.1}そして指数の-30.1を整数部分と小数部分に分けて計算していきます。
\left(\cfrac{1}{2}\right)^{100}=10^{-30.1}=10^{0.9}\times 10^{-31}小数部分の指数は必ず0と1の間になるように分けてください。
（ダメな例：10^{-0.1}\times 10^{-30}）
ここで10^{0.9}がどんな数なのかを探っていきます。
\begin{array}{l}
\log_{10}8\\\\
=\log_{10}2^3\\\\
=3\log_{10}2\\\\
=3\times 0.3010\\\\
=0.9030
\end{array}なので、
10^{0.9030}=8は判明。10^{0.9}はもう少し小さそうです。
次に\log_{10}7を求めたいところですが、\log_{10}7の近似値は、\log_{10}2と\log_{10}3を用いても求めることができません。
そこで、\cfrac{3}{4}=0.75に注目して、\log_{10}7.5を求めてみます。
\begin{array}{l}
\log_{10}7.5\\\\
=\log_{10}(0.75\times10)\\\\
=\log_{10}\left(\cfrac{3}{4}\times10\right)\\\\
=\log_{10}\cfrac{3}{4}+\log_{10}10\\\\
=\log_{10}3-\log_{10}4+\log_{10}10\\\\
=0.47710-0.6020+1\\\\
=0.8751
\end{array}よって、
10^{0.8751}=7.5となりました。
10^{0.9}は7.5と8の間にあるので、「7.△△△…」であることがわかります。
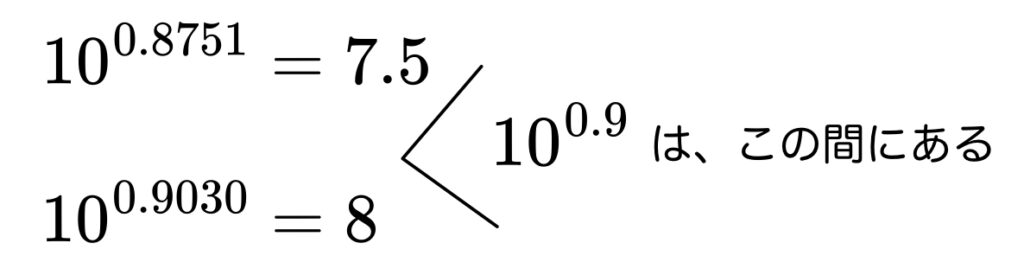
この7.△△△…に10^{-31}をかける、つまり10で31回割れば、\left(\cfrac{1}{2}\right)^{100}になります。
10で31回割るということは、小数点を左に31回動かすということ。
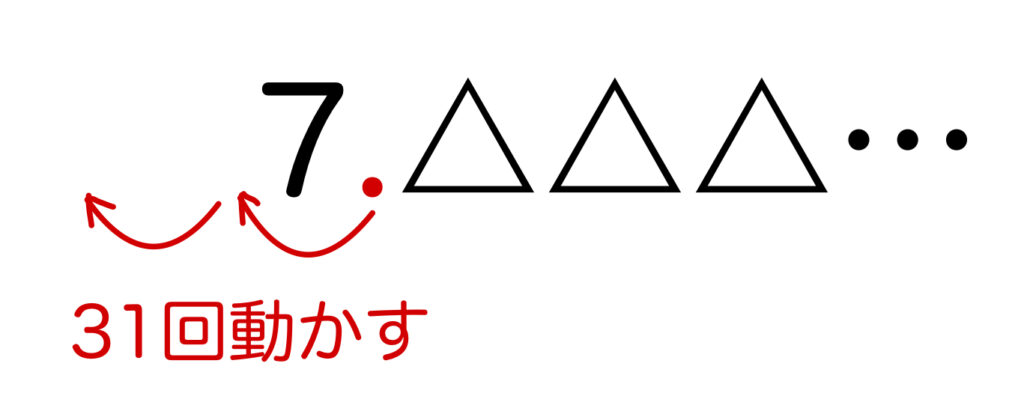
- 小数点を1回動かすと、0.7△△△…で、小数第1位に初めて0でない数が現れる。
- 小数点を2回動かすと、00.7△△…で、小数第2位に初めて0でない数が現れる。
と続くことから、小数点を31回動かすと、小数第31位に初めて0でない数が現れる。
また、「7.△△△…」の小数点を動かしたことから、初めて現れる0でない数は7。
2つの指数に分けるときだけ注意が必要ですが、基本的には桁数の問題と同じ方法で求めることができるんです。
まとめ
この記事では、常用対数を使った桁数の問題を解説しました。
指数の形に直すことで、「桁数」の場合も「小数第何位に初めて0でない数が現れるか」の場合も同じ方法で求めることができます。
ついでに最高位の数字までわかってしまうのでおすすめです。
あなたの持っている教科書や問題集の問題でも実践してみてくださいね！
このブログでは，自分で勉強しているとき，つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や，勉強が楽しくなる文房具も紹介していますので，よろしければご覧ください！
コメント