共通テストが近づいてきましたね。
 学生の方
学生の方数学無理!無理!ヤバイ!助けて!
と思ってるそこのアナタ!
数学難しいですよね。わかります。
だからといって残り日数もそんなにない中で、できることには限りがあります。
そこでこの記事では、共通テストの数学で1点でも多く取るために、これだけは覚えておくといいよ!という、即効性高めのポイントをまとめて紹介します。
共通テスト本番直前にチェックしたい人、数学が苦手でなんでもいいからすがりたい人、ヤバイを通り越してわけがわからなくなってる人、ぜひご覧ください。
【三角関数】半角の公式
三角関数は数IIの中でも特に苦手な人が多いと思います。
数多くある公式の中で、半角の公式は覚えていない人が多い割によく出てくるので、この際暗記でいきましょう。
\begin{array}{ll}
\sin^2\theta&=&\cfrac{1-\cos2\theta}{2}\\\\
\cos^2\theta&=&\cfrac{1+\cos2\theta}{2}
\end{array}半角の公式は、θを2θで表す公式。ということは、次の公式も仲間に入れてあげましょう。
\sin\theta\cos\theta=\cfrac{1}{2}\sin2\thetaこれは2倍角の公式\sin2\theta=2\sin\theta\cos\thetaを移項しただけなんですが,意外とよく出てくるので,
\sin\theta\cos\thetaを見たら\sin2\thetaを疑え!
と思っておきましょう。
【積分】面積の公式(1/6・1/3・1/12)
数II・B・Cで最も配点が大きいとされる微分・積分。
面積の計算は積分が必要になるのでどうしても計算量が多くなりがち。
文字が含まれていたりするとなおさらですよね。
そこで,簡単な形であれば公式一発で面積を出せるようにしておくと,分単位で時間が短縮できます。
詳しくはこちらの記事で説明しています。

2次関数と直線で囲まれる面積(6分の1公式)
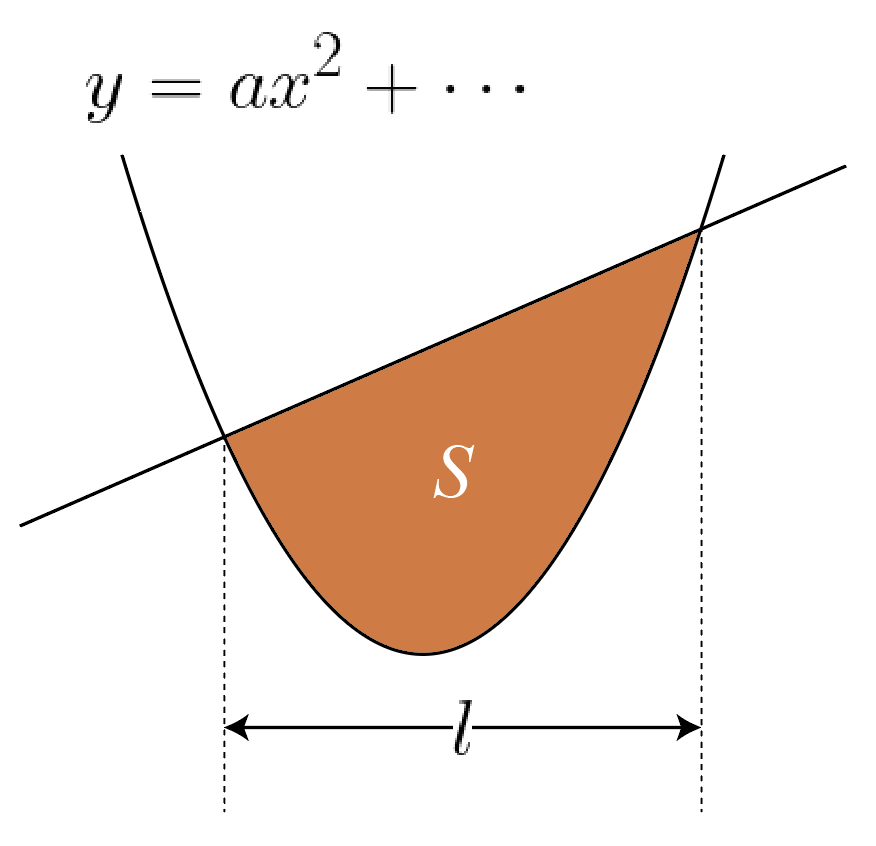
色を付けた部分の面積をSとすると
\large{S=\cfrac{|a|}{6}l^3}2次関数と接線で囲まれる面積(3分の1公式)
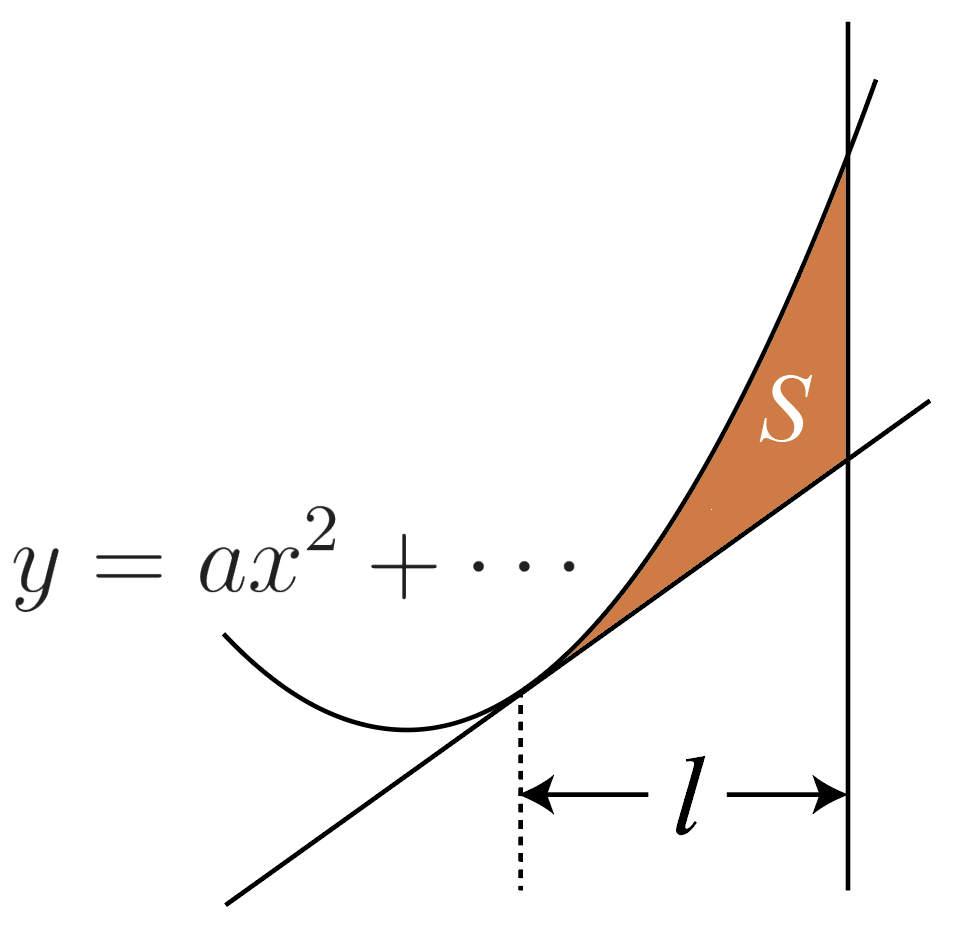
色を付けた部分の面積をSとすると
\large{S=\cfrac{|a|}{3}l^3}2次関数と2つの接線で囲まれる面積(12分の1公式)
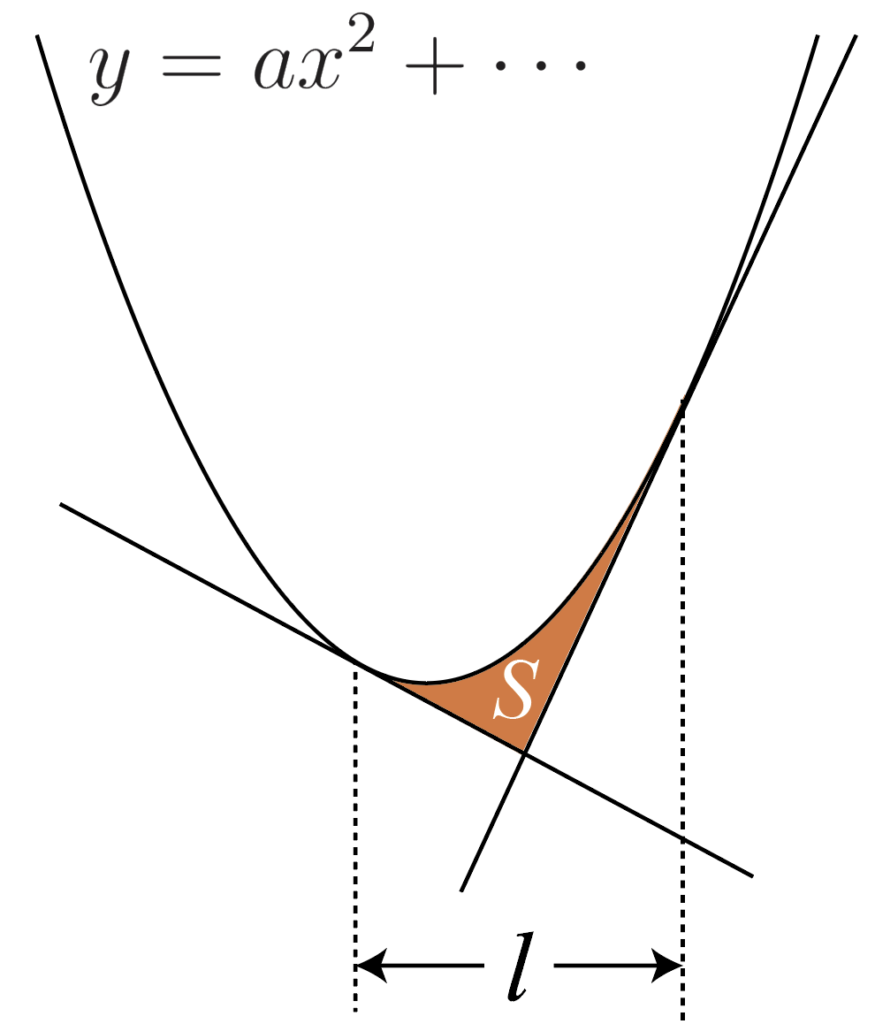
色を付けた部分の面積をSとすると
\large{S=\cfrac{|a|}{12}l^3}いずれの公式も,2次の係数aと横幅lがわかれば面積が求められます。直線の式はわからなくてもいいのが最大のポイント。
最近の出題傾向として,このような公式だけで求められる面積はあまり出ないですが,序盤の問題とかで軽く面積を出さなきゃいけないときなんかに活躍すると思うので,是非覚えておきましょう。
公式が使えない形のときは普通に積分するしかないので,そこはあしからず。
【データの分析】変量の変換
数I・Aで結構ウェイトが高いのがデータの分析。
後半によく出てくる変量の変換。
「全員の点数が2倍になったら平均はどうなる?」
といった類の問題ですね。
本当は変化するしくみも知っておきたいところですが,なにせ時間がないので,覚えてしまいましょう。
こちらも詳しく説明している記事がありますので,気になる方はどうぞ。

ax+bの平均
変量xに対して新しい変量u=ax+bを定める。
uの平均を\overline{u},xの平均を\overline{x}とすると,
\large \overline{u}=a\overline{x}+b全員の点数が2倍になれば平均も2倍になるし,全員の点数が5点上がれば平均も5点上がるので,感覚的にも理解しやすいかと思います。
ax+bの分散
変量xに対して新しい変量u=ax+bを定める。
uの分散を{S_u}^2,xの分散を{S_x}^2とすると,
\large {S_u}^2=a^2{S_x}^2分散に影響するのは「何倍になったか」だけであり,「何を足したか」は分散に影響を与えません。
ax+bの標準偏差
変量xに対して新しい変量u=ax+bを定める。
uの標準偏差をS_u,xの標準偏差をS_xとすると,
\large S_u=|a|S_x
分散と同様「何倍になったか」だけが影響を与えます。標準偏差は|a|倍になります。
ax+bとcx+dの共分散
変量xに対して新しい変量u=ax+b,変量yに対して新しい変量v=cx+d定める。
uとvの共分散をS_{uv},xとyの共分散をS_{xy}とすると,
\large S_{uv}=acS_{xy}変換された変量の共分散は、もとのac倍になります。
ax+bとcy+dの相関係数
変量xに対して新しい変量u=ax+b,変量yに対して新しい変量v=cx+d定める。
uとvの標準偏差をr_{uv},xとyの標準偏差をr_{xy}とすると,
\large
\left\{
\begin{array}{ll}
ac> 0のとき,&r_{uv}=r_{xy}\\\\
ac<0のとき,& r_{uv}=-r_{xy}
\end{array}
\right.もとの変量が何倍されていても相関係数が-1以上1以下の値をとることには変わりがないので,新しい変量の相関係数は,基本的にはもとの相関係数と同じになります。
ただし,acが負の場合は,相関係数の符号が逆になることだけは注意しましょう。
【確率分布と統計的推測】母平均・母比率の信頼区間
数II・B・Cの選択問題は4問から3問選択ですが,文系のあなたは第7問の単元を習っていないので,選択の余地なく4・5・6を解くことになります。
その中で比較的点を取りやすいのが「確率分布と統計的推測」の単元(おそらく第5問)。
後半に出てくる「信頼区間」を求めるところがまあまあ複雑ですよね。
これも形が決まってるので,よくわかってない人は暗記でいきましょう。
詳しいことはこちらの記事で説明しているよ。

まずは母平均の場合。
標本平均を\overline{X},母標準偏差を\sigmaとする。
標本の大きさ n が十分に大きいとき,母平均 m に対する信頼度95%の信頼区間は,
\overline{X}-1.96\cdot\cfrac{\sigma}{\sqrt{n}}\leqq m\leqq\overline{X}+1.96\cdot\cfrac{\sigma}{\sqrt{n}}母標準偏差\sigmaが出てない場合は標本標準偏差で代用可能ですが,たぶん問題用紙に書いてあります。
続いて母比率の場合です。見た目が違うだけで,やってることは母平均のときと同じです。
標本の大きさ n が十分に大きいとき,標本比率を R とすると,母比率 p に対する信頼度95%の信頼区間は,
R-1.96\cdot\sqrt{\cfrac{R(1-R)}{n}}\leqq p\leqq R+1.96\cdot\sqrt{\cfrac{R(1-R)}{n}}この1.96という数字は,信頼区間95%のときに使います。95%が出るのがほとんどなので,1.96も暗記しましょう。
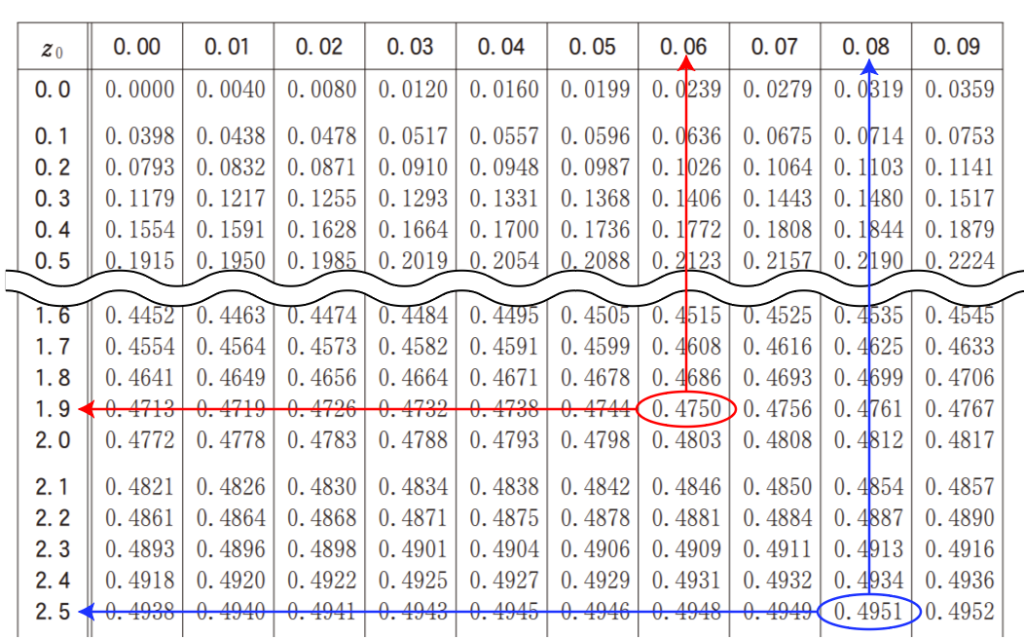
なお,1.96の根拠は,0.95(95%)の半分の0.4750を正規分布表で探すと出てくる数字です。
これが例えば「信頼区間99%」になったら,0.99(99%)の半分0.4950を正規分布表で探したいところですが,ちょうど0.4950は載ってないので,0.4951に対応する2.58を使うことになるかと思います(0.4949を使うと信頼区間が99%よりも狭くなってしまうため。いずれにしても問題文に書かれるはず)。
【図形】円に内接する四角形の性質の逆で円を探す
円に内接する四角形の向かい合う角の和が180°であることは中学校でも習うので知っていると思いますが,逆も成り立つことを忘れがち。
同一円周上にある点が見つかることで話が進んでいくことが結構あるので要注意。
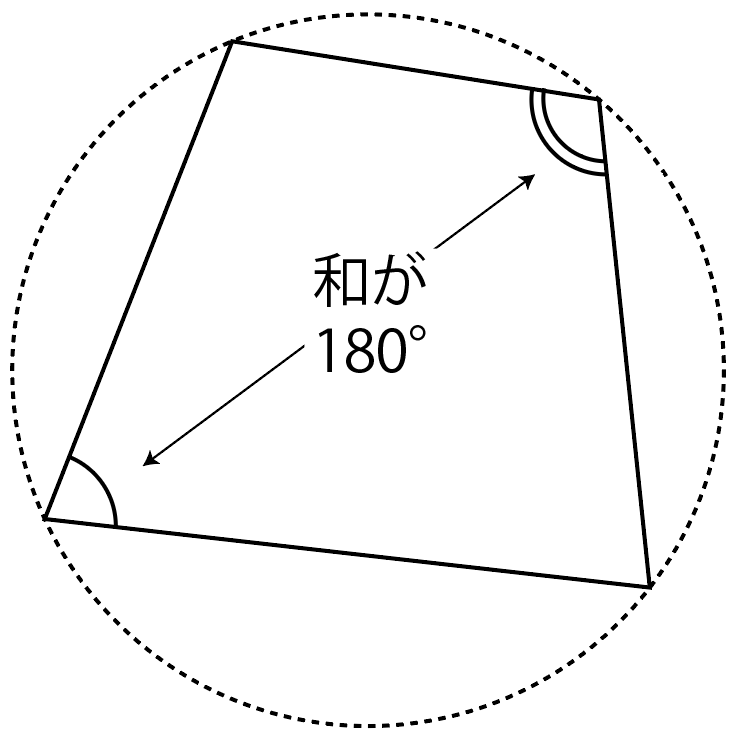
向かい合う角の和が180°のとき,この四角形は円に内接する。
つまり,この四角形をつくる4点は同一円周上にある。
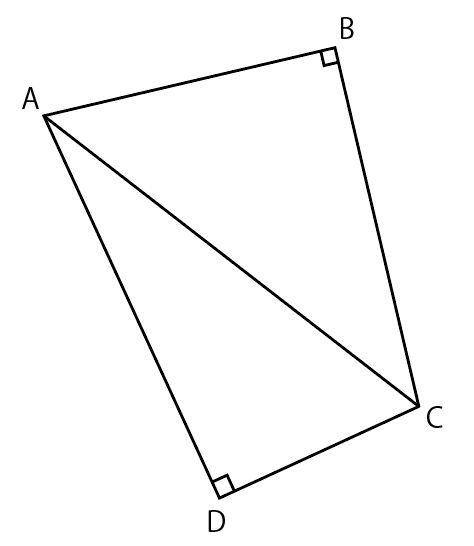
特にやばいのが直角が2つ見つかったときに円が描けるかどうか。
例えば次のような状況のとき,この4点A,B,C,Dって同一円周上ですよ。
 学生の方
学生の方???
∠ABCと∠ADCが両方とも直角ってことは,足したら180°。
向かい合う角の和が180°っていうことは,四角形ABCDは円に内接するっていうこと。
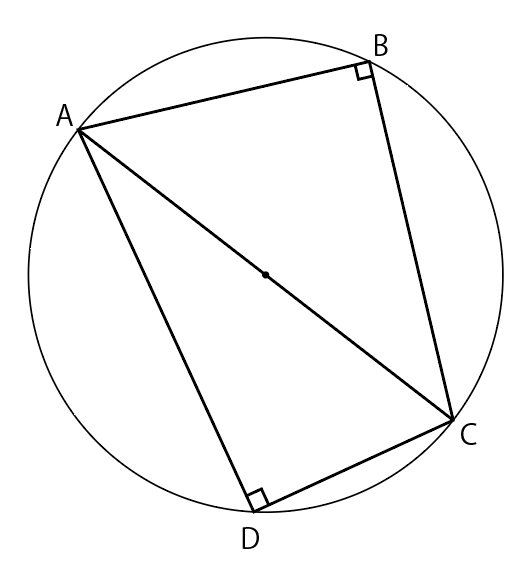
つまり4点A,B,C,Dは同一円周上にあるってことですね。
さらに直径に対する円周角は直角であることも考えると,この円の直径はACであることまでわかってしまいます。
直角三角形がくっついている状況だと,どうしても三角形にばかり目が行ってしまうと思いますが,直角が向かい合った四角形という視点に変換できると,幅が広がりますよ。
自分を信じて、最後の一歩を踏み出そう!
数学が苦手でも、今まで学んできた公式やポイントをきっちり押さえておけば、必ずや得点アップの道は開けます。
どんなに「ヤバイ!」と思っても、公式を思い出して使えるところを一つひとつ探ってみてください。
あなたが今まで積み重ねてきた努力は、確実に実力として残っています。
試験当日は焦らず、目の前の問題に集中していきましょう。
結果がどう転んでも、成長は必ずあなたに返ってきます。
自分を信じて、最後まで走りきるのみ!

