数Ⅱの最後の単元「積分」では,面積の計算が出てきます。
「上から下を引いて積分」という手順そのものが難しいということはありません。
 学生の方
学生の方時間があればできるけど,模試だと時間がたりなくなちゃうよ。
真面目に積分していくと計算が大変で嫌になっちゃうよ…という経験はありませんか?
この記事では,面積の計算スピードを上げるための便利な公式5つを紹介します。

粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。
積分を用いた面積の計算とは
複数の直線や曲線で囲まれる部分の面積は,ふつうは積分を用いて求めます。
例えばこんな問題。
放物線y=x^2-2と直線y=-2x+1で囲まれる部分の面積を求めよ。
まずは図を書くために,放物線と直線の交点を求めます。
放物線と直線の式を連立させて,
x^2-2=-2x+1
⇔ x^2+2x-3=0
⇔ (x-1)(x+3)=0
∴ x=-3,1
となるので,放物線と直線の交点のx座標は-3,1
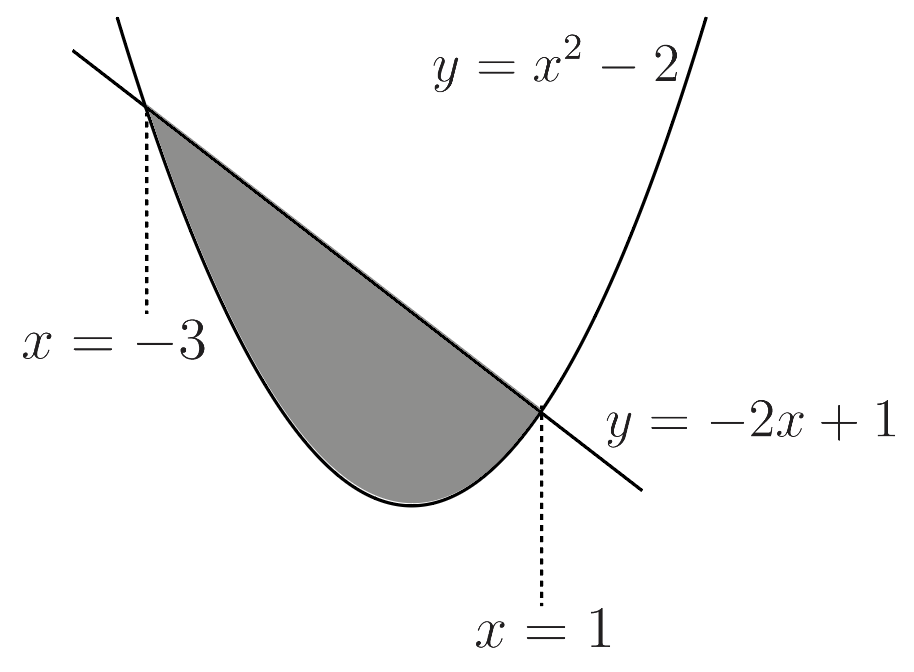
面積は「上から下を引いて積分」なので,
\displaystyle \int^1_{-3}\{(-2x+1)-(x^2-2)\}dx
= \displaystyle \int^1_{-3}(-x^2-2x+3)dx
= \left[-\cfrac{1}{3}x^3-x^2+3x\right]^1_{-3}
= \left(-\cfrac{1}{3}\cdot 1^3-1^2+3\cdot 1\right)-\left\{-\cfrac{1}{3}\cdot(-3)^3-(-3)^2+3\cdot(-3)\right\}
= \cfrac{32}{3}
 学生の方
学生の方めんどくさいし,間違えそう…
積分の計算をまともに行うと,分数が出てきて,計算がとても煩雑になりがちです。
そこで,特定の形においては,面積の計算公式を覚えておくことで,計算にかかる時間を大幅に減らすことができます。
計算スピード爆上がり!面積の計算公式5選
ここからは,積分の問題でよく出される面積の計算公式を5つ紹介します。
2次関数と直線で囲まれる面積(6分の1公式)
もっともよく使われるのが「2次関数と直線で囲まれる部分」の面積です。
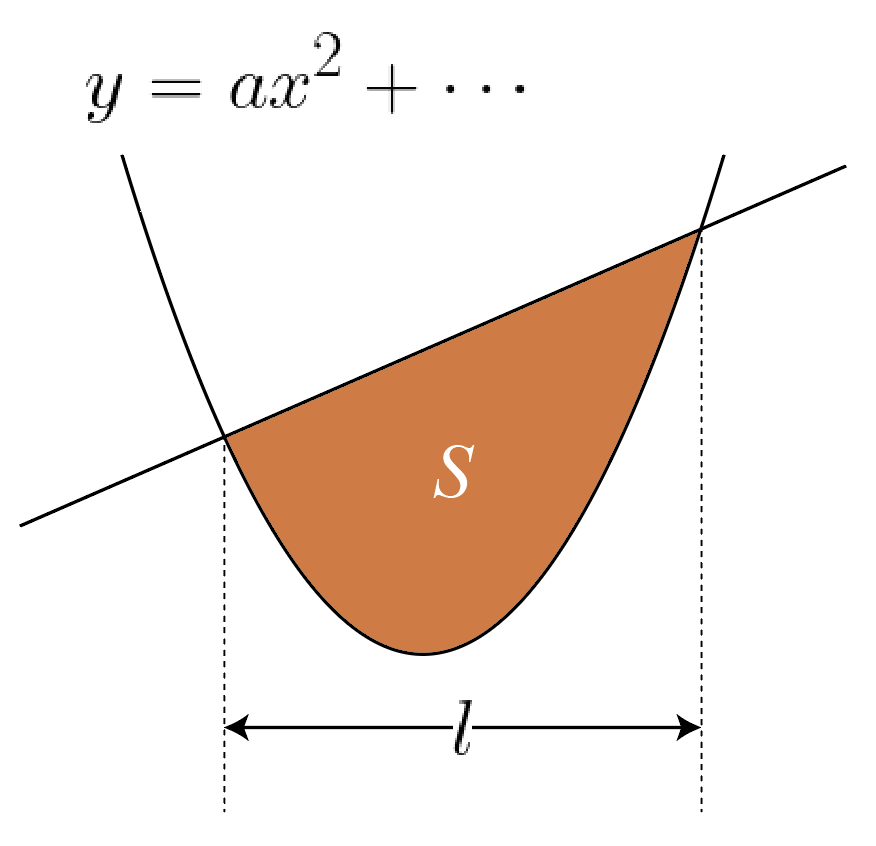
図の色を付けた部分の面積をSとすると,
S=\cfrac{|a|}{6}l^3
面積を求めるのに必要なのは,「2次の係数」と「横幅」だけ。
そして直線の式は何でもよい!ということです。
上の例題でやってみましょう。
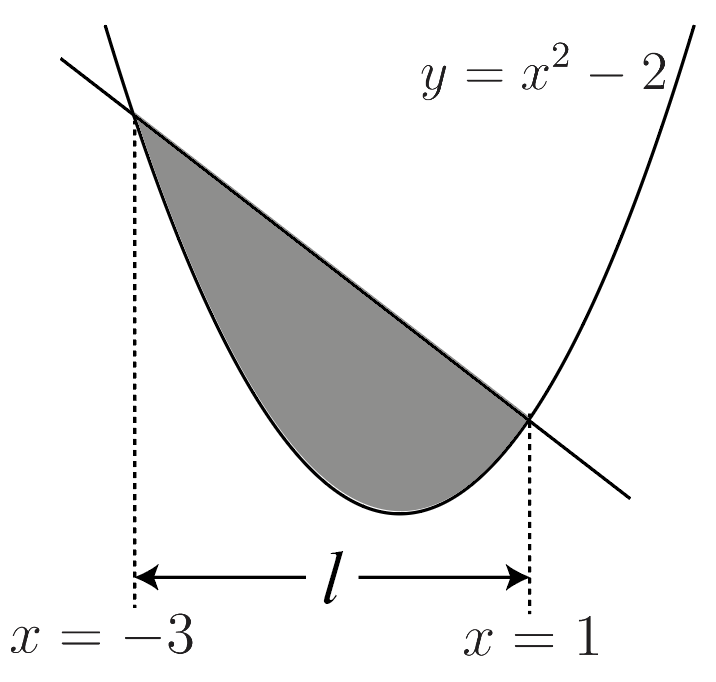
(放物線と直線の交点を求めるところまでは上の解答と同じ)
aは2次の係数なので,1
lは横幅なので,1-(-3)=4
よって,色を付けた部分の面積は,
\cfrac{|1|}{6}\cdot 4^3
=\cfrac{32}{3}
 学生の方
学生の方速い…速すぎる…
答えを求めるだけなら,公式一発で計算してしまえるのは強いです。
2次関数と2次関数で囲まれる面積(6分の1公式)
2次関数と2次関数でで囲まれる部分の面積も,6分の1公式が使えます。
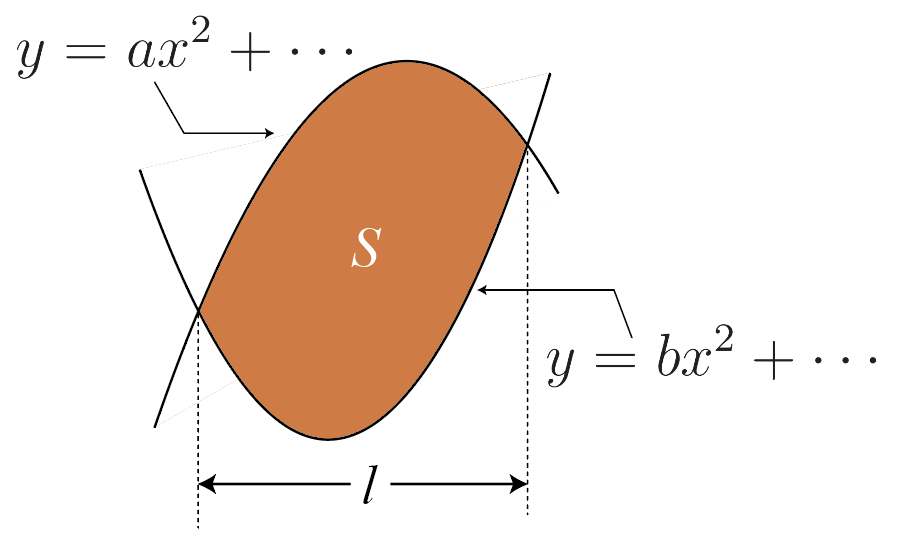
図の色を付けた部分の面積をSとすると,
S=\cfrac{|a-b|}{6}l^3
分母が「2次の係数の差」になるところに注意しましょう。
2次関数と接線で囲まれる面積(3分の1公式)
2次関数とその接線で囲まれる部分の面積は,分母が3になります。
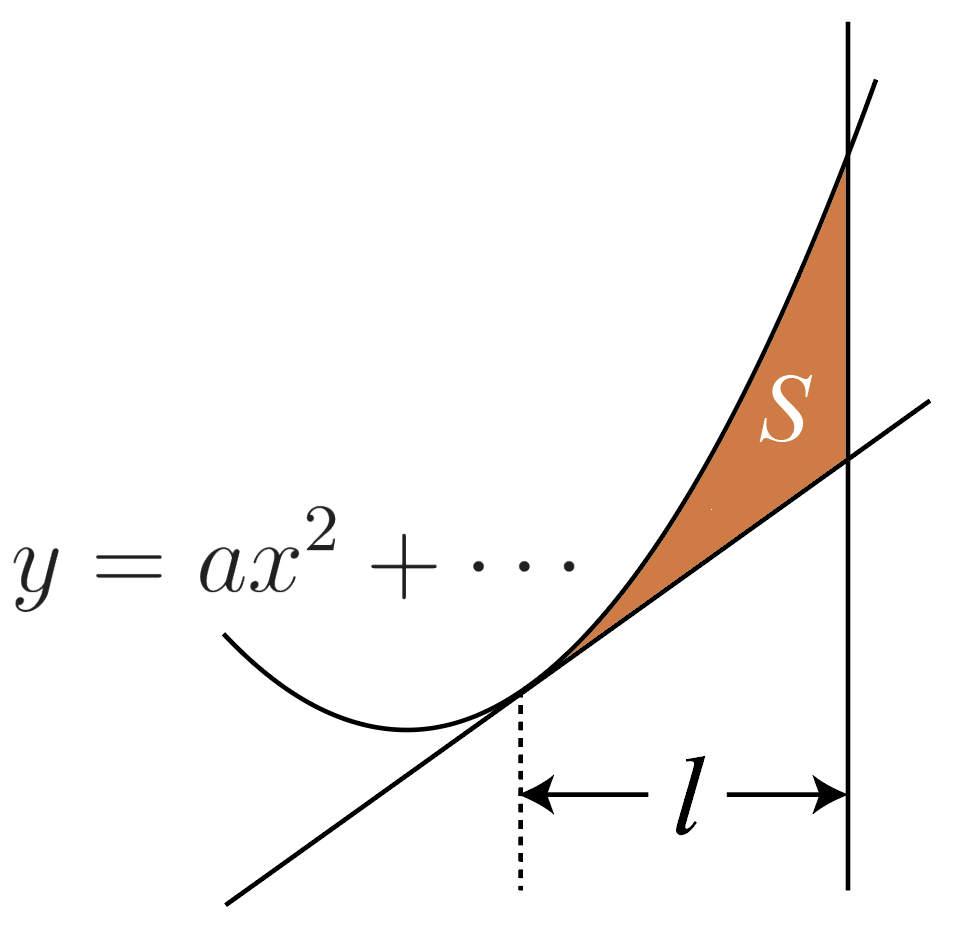
図の色を付けた部分の面積をSとすると,
S=\cfrac{|a|}{3}l^3
接点は右側でも左側でもいいです。例を1つ。
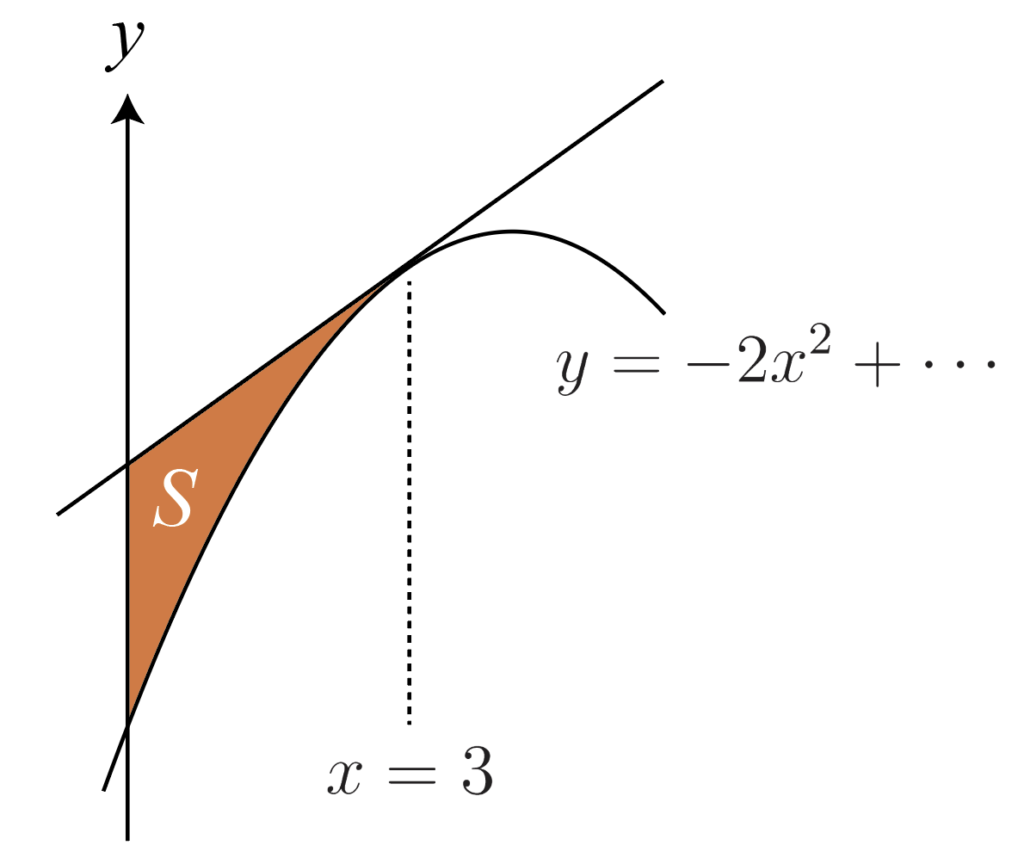
色を付けた部分の面積は,
\cfrac{|-2|}{3}(3-0)^3
=\cfrac{2}{3}\times 3^3
=18
求めているのは面積なので,必ず正の値になることは確認しておきましょう。
2次関数と2本の接線で囲まれる面積(12分の1公式)
2次関数と2接線で囲まれる面積は頻出ですが,公式を知らないと時間がかかってしまいます。
分母が12になります。
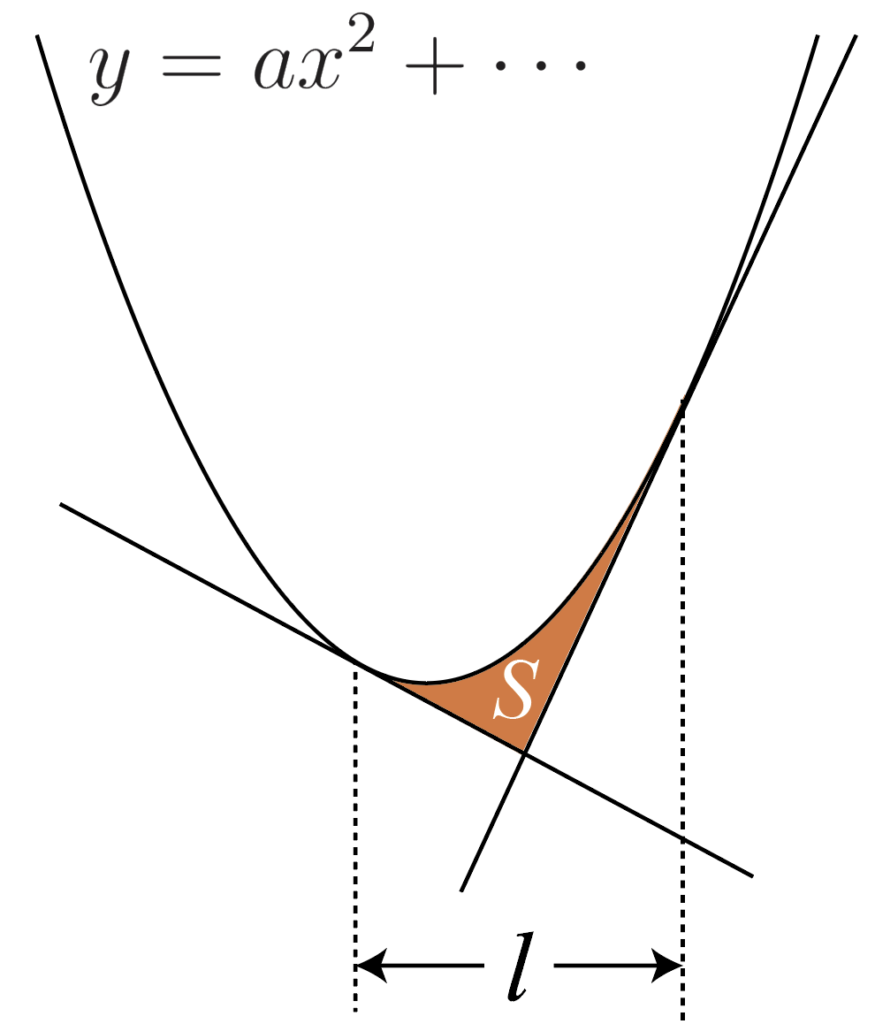
図の色を付けた部分の面積をSとすると,
S=\cfrac{|a|}{12}l^3
ひとつ例をあげます。公式と違って見えますが,実は同じです。
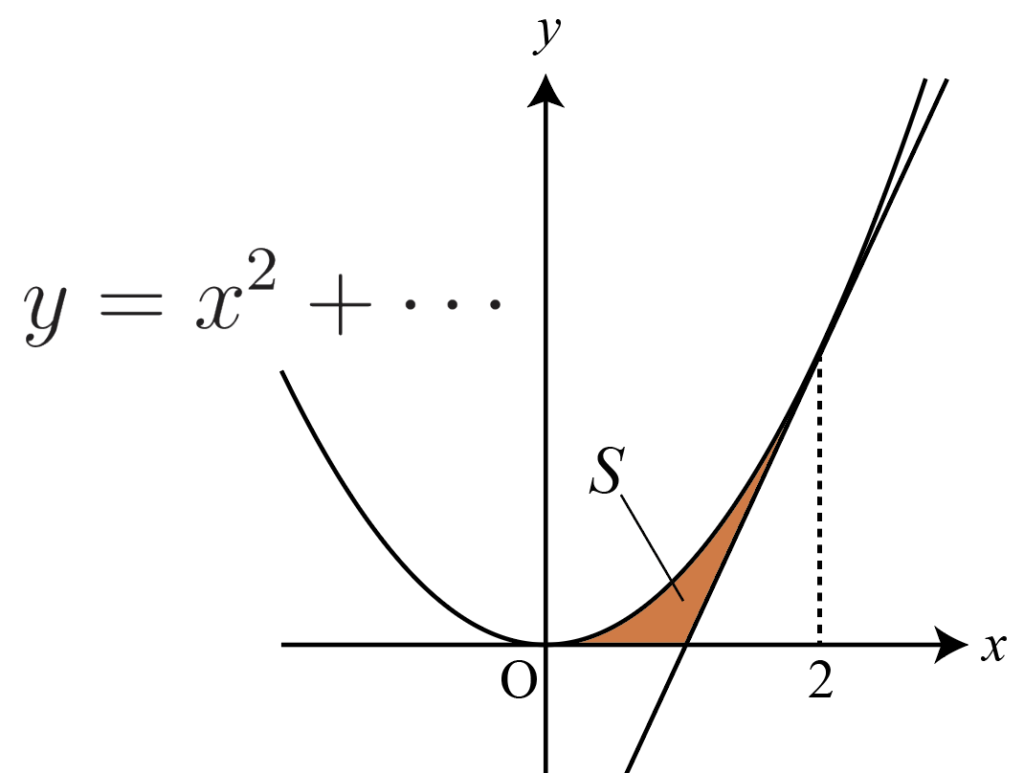
図の色を付けた部分の面積は,
\cfrac{|1|}{12}(2-0)^3
=\cfrac{1}{12}\times 8
=\cfrac{2}{3}
一見,接線が1つしかないように見えますが,今回はx軸も接線とみなすことができますよね。
よって,2つの接線で囲まれた形が使えることになります。
3次関数と接線で囲まれる面積(12分の1公式)
最後に3次関数と接線で囲まれる面積です。
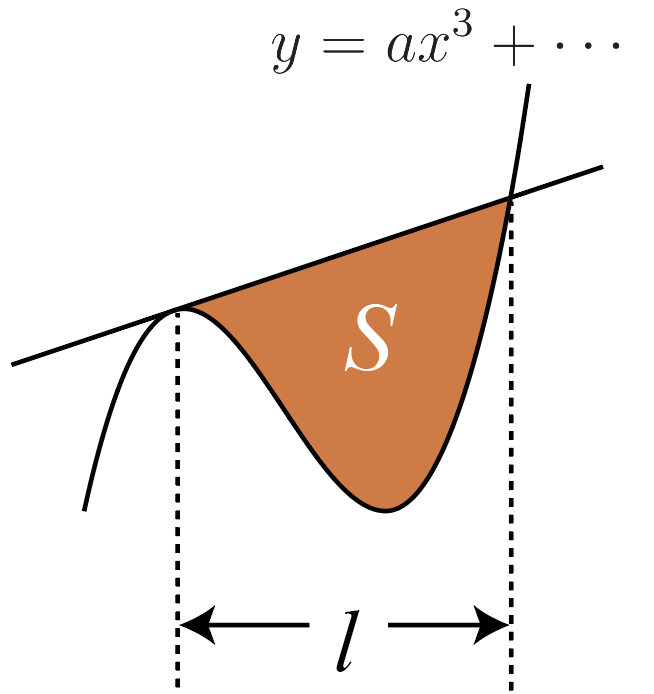
図の色を付けた部分の面積をSとすると,
S=\cfrac{|a|}{12}l^4
こちらも12分の1ですが,4乗になっていることに注意してください。
積分の面積公式を使う上での注意点
とても便利な積分の面積公式ですが,使う上で注意しておかなければならないことがあります。
- 公式がそのまま使えないことが多い
- 記述の解答では書きづらい
- 本来の積分を忘れてしまいそう
順に説明していきますね。
注意点① 公式がそのまま使えないことが多い
実際の入試問題は,公式をそのまま使って面積が求められることは多くありません。
例えば次のような面積。
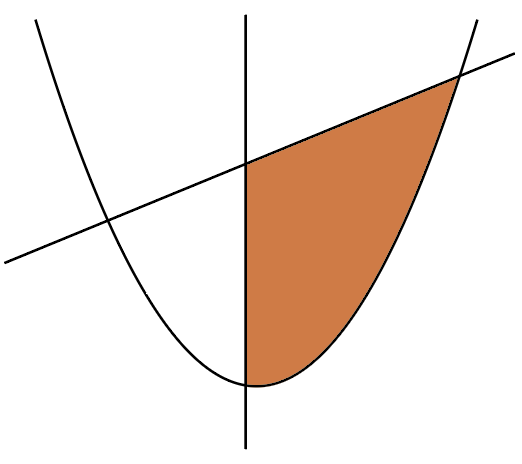
一見,「6分の1公式」が使えそうに見えるかもしれませんが,直線部分が2本あるので,公式は使えません。
公式が使えない場合は,本来の求め方に戻って,「(上の線の式)ー(下の線の式)」を積分して計算するのが,結局早いです。
どうしても積分をしたくないという人は,次の図のように2つに分けて求めることもできます。
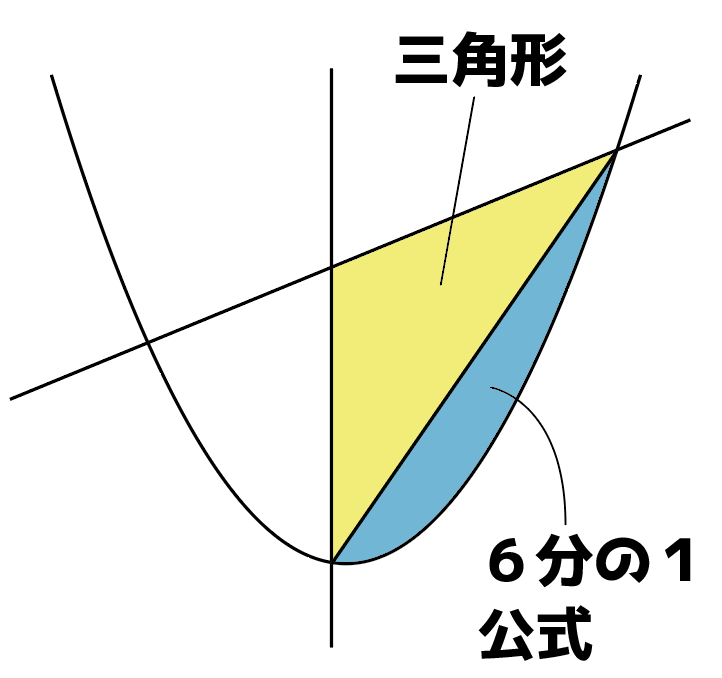
上の黄色い部分は三角形なので,三角形の面積(底辺✕高さ÷2),下の青い部分は「6分の1公式」で求められるので,
それぞれを計算して足せば,面積が求められます。
 粗茶さん
粗茶さんここまでするぐらいなら,普通に積分したほうがいいかもしれない…
注意点② 記述の解答では使いづらい
積分の面積公式は,記述式の解答に説明無しで使うことはできません。
導出過程も採点の対象になる記述問題で,いきなり公式を書いて答えにするのはマズイでしょう。
どうしても公式で計算したい場合であっても,とりあえずインテグラルをつかった式は書いて,最低限「積分したふり」はしておきましょう。
\displaystyle \int^1_{-3}\{(-2x+1)-(x^2-2)\}dx
=\cfrac{|1|}{6}\{1-(-3)\}^3
=\cfrac{32}{3}
 粗茶さん
粗茶さん限りなく黒に近いグレーのような気がする…
積分の「6分の1公式」だけは,教科書で扱われているので,証明無しで使っても許される可能性が高い。
\displaystyle\int^{\beta}_{\alpha}(x-\alpha)(x-\beta)dx=-\cfrac{1}{6}(\beta-\alpha)^3
注意点③ 積分のやりかたを忘れてしまいそう
便利な公式だけを使っていると,本来の積分のやり方を忘れてしまうかもしれません。
2次関数と直線でつくられる面積であれば,工夫をこらすことで,大抵の問題は積分なしで求めることができます。
しかし,最近のセンター試験・共通テストでは,積分の計算そのものを問う出題も増えています。
裏技的な公式だけに頼らず,積分の計算もきちんとできるようにしておきましょう。
 粗茶さん
粗茶さんもちろん数Ⅲまで必要な人は,積分あります。
積分の面積公式 まとめ
今回は,面積の計算スピードを上げるための便利な公式を5つ紹介しました。
微分・積分の分野は,数ⅡBの中では比較的得点しやすい分野だと思います。
面積の計算はどうしても数が複雑になるので,便利な公式を併用しつつ,効率よく解き進めていきましょう!
積分の面積公式 おすすめ参考書
面積の公式以外にも,共通テストで即効性の高い解き方が満載!
このブログでは,自分で勉強しているとき,つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や,勉強が楽しくなる文房具も紹介していますので,よろしければご覧ください!




