今回は「円の接線の方程式」のお話です。
円の接線の求め方って，なんだか文字が多くなってごちゃごちゃすると思っていませんか？
実は，円の接線の方程式は，文字１つをおくことで求めることができてしまいます。
・円の接線の方程式を，1つの文字をおくだけで求めることができる。
- 高校数学・高校公民・中学社会担当の現役塾講師
- 講師歴13年
- 13年の指導経験で知った「生徒がつまづきやすいポイント」や「教科書よりも効率の良い解法」をわかりやすく発信しています。
予備知識
円の接線とは
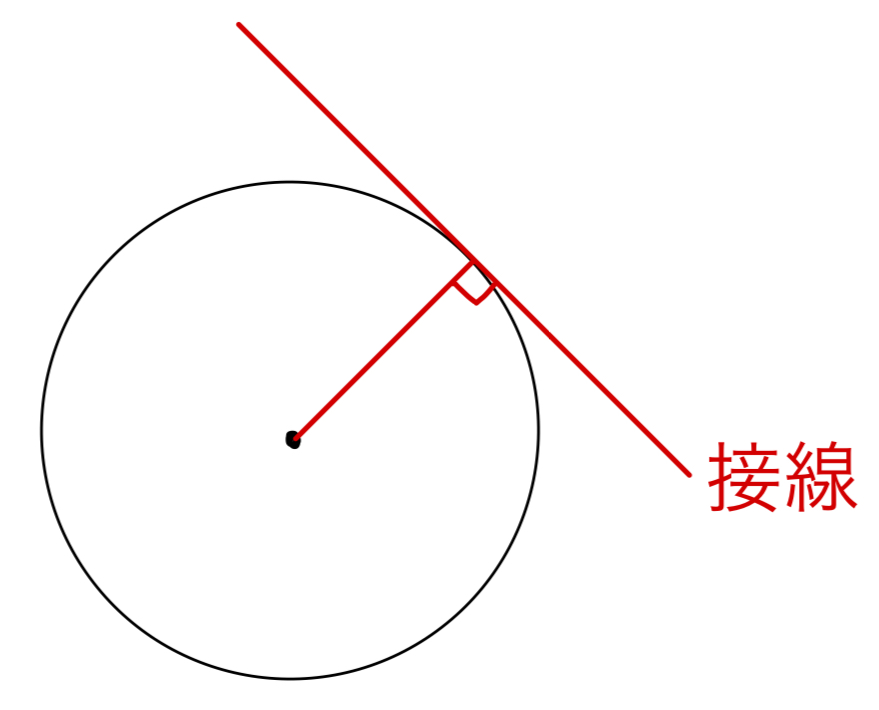
円の接線とは，円に接している（１点を共有する）直線のことです。
円の中心と接点を結んだ直線は，接線と垂直に交わるという性質があります。
直線の方程式
直線の方程式は，「傾き」と「通る点」がわかれば，求めることができます。
傾きがmで点(p,q)を通る直線の方程式は
y-q=m(x-p)
例えば，傾きが2で，点(1,3)を通る直線は，
y-3=2(x-1)
\therefore y=2x+1
のように求められます。
円の接線を求めよう
それでは，円の接線を求めていきましょう。
原点が中心の円で，接点がわかっている場合
もっとも易しいパターンです。
円 x^2+y^2=25の、点(4,3)における接線の方程式を求めよ。
「点(4,3)における」とは、「点(4,3)が接点ですよ」ということなので，図はこんな感じになります。
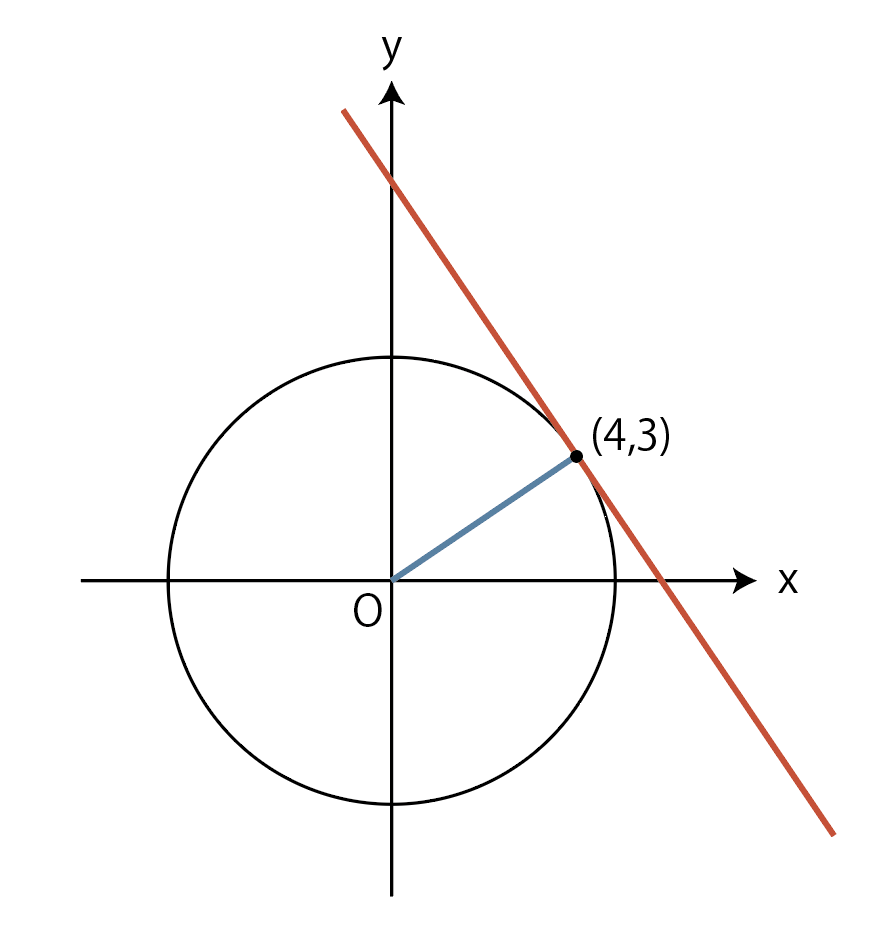
原点が中心の円で，接点がわかっている場合は、文字をおく必要もありません。
円の中心と接点を結ぶ直線（上図の青い線）の傾きは\cfrac{3}{4}
これが接線と垂直になっていることから、接線の傾きを求めることができます。
ここで使う公式がこちら。
傾きmの直線と傾きnの直線が垂直に交わるとき、
mn=-1 すなわち、n=-\cfrac{1}{m}
傾きを逆数にしてマイナス倍すると、垂直な直線の傾きになります。
今回の場合は、青い線の傾きが\cfrac{3}{4} なので、接線の傾きは-\cfrac{4}{3}
もちろん接点(4,3)を通ります。
というわけで求める接線は、傾き-\cfrac{4}{3}で、(4,3)を通る直線なので、
y-3=-\cfrac{4}{3}(x-4)
よって，y=-\cfrac{4}{3}x+\cfrac{25}{3} …（答）
ただ，原点が中心の円の接線については，次の公式があります。
円x^2+y^2=r^2の，点(a,b)における接線の方程式は，
ax+by=r^2
今回の場合だと，円の式がx^2+y^2=25，接点が(4,3)だったので，公式にあてはめると，接線の方程式は，
4x+3y=25
よって，y=-\cfrac{4}{3}x+\cfrac{25}{3}
となります。さっきと同じです。
中心が原点の場合については，この公式でやったほうが早いことが多いです。
接点がわからないけど，他の点がわかっている場合
大抵の問題は，接点はわかっておらず，代わりに他の通る点が与えられています。
点(3,1)を通り，円x^2+y^2=2に接する直線の方程式を求めよ。
接点がわかっていない場合は，傾きをmとおいて，とりあえず直線の式をつくります。
接線の傾きをmとすると，求める接線は，
点(3,1)を通り，傾きmの直線だから，
y-1=m(x-3)すなわち，y=mx-3m+1 …①
となります。
ここで必殺！「点と直線の距離」公式が登場します。
点(p,q)と直線ax+by+c=0の距離をdとすると，
d=\cfrac{|ap+bq+c|}{\sqrt{a^2+b^2}}
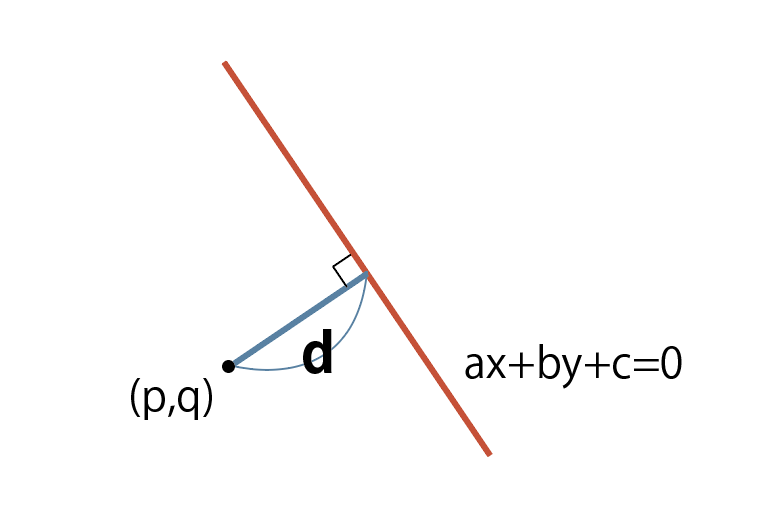
実は，円の中心と接線の距離は，円の半径と同じになります。
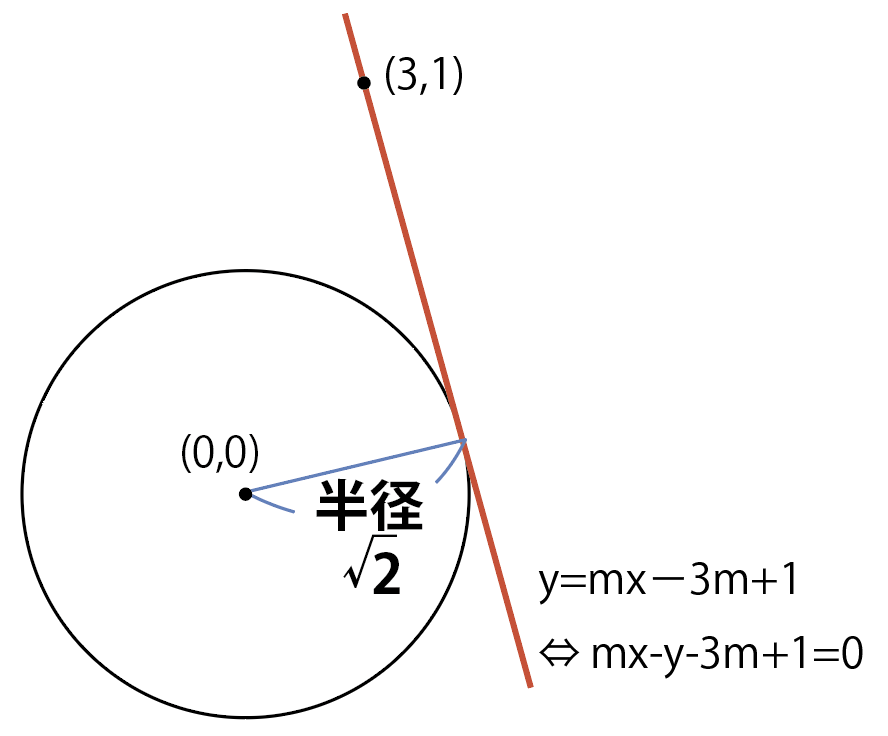
つまり「円の中心(0,0)と接線mx-y-3m+1=0の距離」＝「半径」という方程式を作って解けば，mがわかって，接線が求められるという流れができあがります。
点と直線の距離の公式を使うとき，直線の式は必ずax+by+c=0の形で使います。
今回も，①の式を整理して，mx-y-3m+1=0という形に直してから使ってね。
円の中心と接線の距離は，円の半径に等しいので，
\cfrac{|m\cdot 0-0-3m+1|}{\sqrt{m^2+1^2}}=\sqrt{2}
両辺を\sqrt{m^2+1}倍しつつ計算して，
|-3m+1|=\sqrt{2(m^2+1)}「絶対値」＝「ルート」のときは，両辺が正の数なので，両辺を2乗しても問題ありません。
両辺を2乗して，
(-3m+1)^2=2(m^2+1)
\Leftrightarrow 9m^2-6m+1=2m^2+2
\Leftrightarrow 7m^2-6m-1=0
\Leftrightarrow (7m+1)(m-1)=0
\therefore m=-\cfrac{1}{7}，1
それぞれを①に代入して，求める接線は，
y=-\cfrac{1}{7}x+\cfrac{10}{7}，y=x-2 …（答）
ここで紹介した方法ではなく，接点を(x_1,y_1)などとおいて，連立方程式をつくる方法が常套手段とされていますが，連立方程式がめんどくさいので，個人的には傾きをｍと置く方法をおすすめします。
ただし，傾きをｍとおく方法には，１つだけデメリットがあります。
円外の点から引いた接線は必ず2本あるので，ｍも2つ出てくるはずです。
しかし，問題によってはｍが１つしか出てこない場合があります。
ｍが1つしか出ないときは，1つの接線の傾きが定義できない，つまりy軸に平行な直線になっているということです。
例えばこんな感じ。
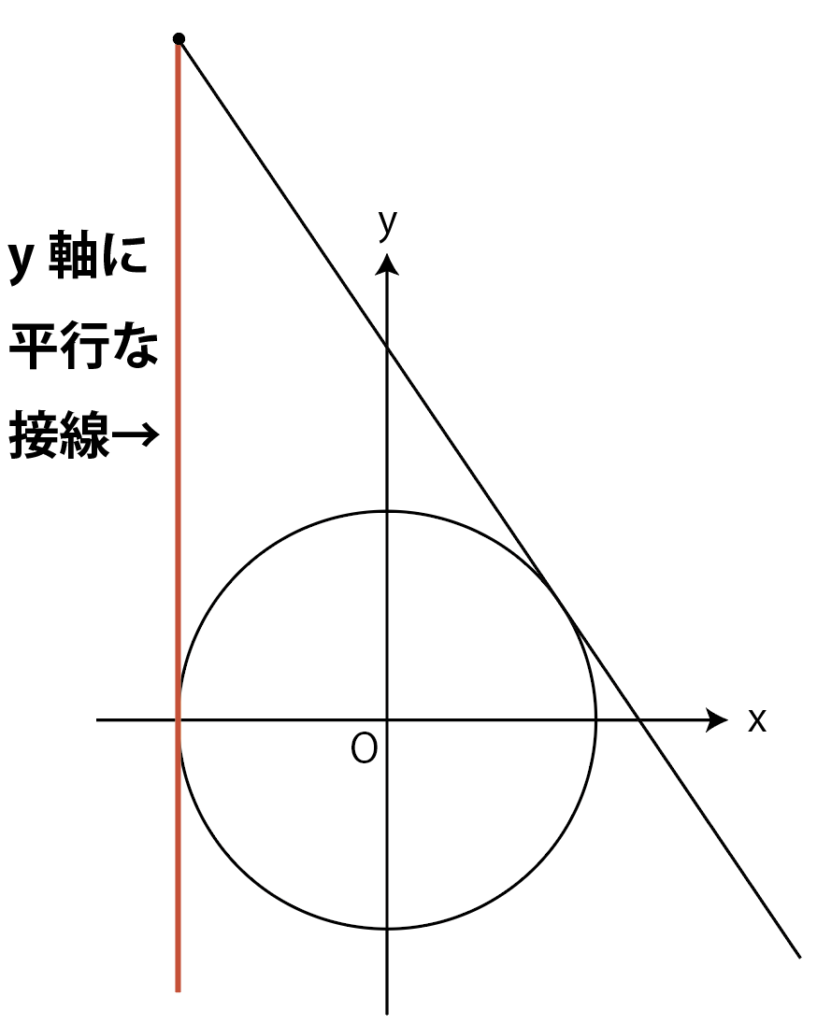
ｍが1つしか求まらなかった場合は，上図の赤線のような接線が存在しているので，図を描いて示しておきましょう。
原点以外が中心の円
最もめんどうなパターンとされています。
しかし，傾きをmとおく方法を使えば，中心がどこにあってもやり方は変わりません。
点(2,4)を通り，円(x+2)^2 +(y-2)^2 =10に接する直線の方程式を求めよ。
例題2と同じように，傾きをmとおいて，接線の方程式を作ります。
接線の傾きをmとすると，求める接線は，
点(2,4)を通り，傾きmの直線だから，
y-4=m(x-2)すなわち，mx-y-2m+4=0 …①
粗茶さんこのあと「点と直線の距離」の公式をつかうので，最初からax+by+c=0の形にしておきました。
続いて，「円の中心(-2,2)と接線mx-y-2m+4=0の距離」＝「半径」という方程式を作って解けばOK。
中心の座標が原点ではなく(-2,2)になっただけで，やり方は同じです。
円の中心と接線の距離は，円の半径に等しいので，
\cfrac{|m\cdot(-2)-2-2m+4|}{\sqrt{m^2+1^2}}=\sqrt{10}
両辺を\sqrt{m^2+1}倍しつつ計算して，
|-4m+2|=\sqrt{10(m^2+1)}両辺を2乗して，
(-4m+2)^2=10(m^2+1)
\Leftrightarrow 16m^2-16m+4=10m^2+10
\Leftrightarrow 3m^2-8m-3=0
\Leftrightarrow (3m+1)(m-3)=0
\therefore m=-\cfrac{1}{3}，3
m=-\cfrac{1}{3}のとき，①は，
-\cfrac{1}{3}x-y+\cfrac{14}{3}
\Leftrightarrow x+3y-14=0
m=3のとき，①は，
3x-y-2=0
よって，求める接線は，
x+3y-14=0，3x-y-2=0 …（答）
一応，中心が原点ではない円の接線の公式というのもあるんですが…
円(x-p)^2+(y-q)^2=r^2上の点(a,b)における接線の方程式は
(a-p)(x-p)+(b-q)(y-q)=r^2
覚えてもいいと思うんですが，結局接点を文字でおかないといけないので，連立方程式を解くはめになります。
べ，別にいいんだけど連立方程式でも。
まとめ
円の接線の求め方のうち，おく文字をできるだけ少なくするやり方を紹介しました。
- 接線の傾きをmとおいて，接線の方程式をつくる。
- 「中心と接線の距離」＝「半径」で，ｍの方程式をつくって解く
- ｍを接線の式に代入して完成
- ｍが１つしか出ないときは，１つの接線がy軸に平行なので注意
数Ⅱは単元が多いので，暗記することはできるだけ少なくして，効率よく習得していきましょう！
図形と方程式 おすすめ参考書
信頼と実績の坂田先生です。
ポチップ
このブログでは，自分で勉強しているとき，つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や，勉強が楽しくなる文房具も紹介していますので，よろしければご覧ください！
コメント