「点と直線の距離」を使う状況に出くわした時、うっ,思い出せない…と思ったことはありませんか?
実は「点と直線の公式」は慣れてしまえば忘れることはなくなります。
複雑そうな式も、一つひとつの意味をしっかり押さえれば、自然と覚えられてしまうからです。
この記事では,点と直線の距離の公式の覚え方をわかりやすく説明します。
点と直線の距離は,覚えづらい割に使用頻度が高いので,しっかりマスターしていきましょう!
- 点と直線の距離公式の意味がわかる
- 点と直線の距離公式が覚えやすくなる
- ついでに証明のしかたもわかる

粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

点と直線の距離とは
点と直線の距離の公式とは,こちらです。
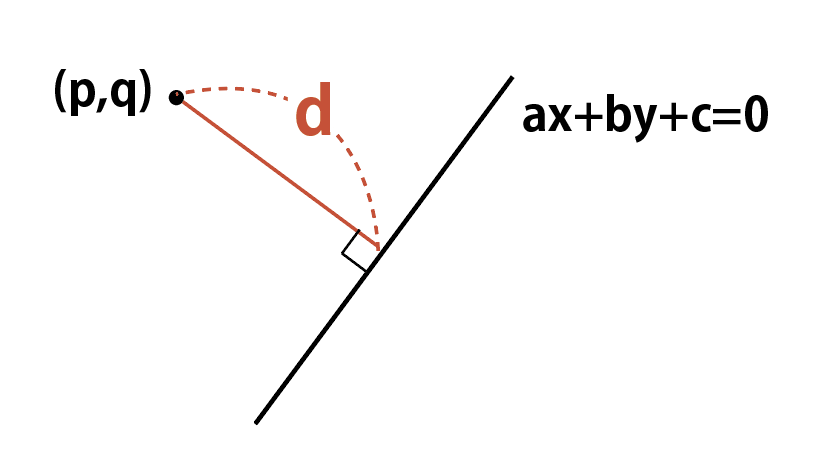
点(p,q) と,直線 ax+by+c=0 の距離を d とすると,
d=\cfrac{|ap+bq+c|}{\sqrt{a^2+b^2}}
個人的には,数Ⅱ・Bの中で,学習者にとって「最悪」の公式だと思っています。
なぜなら点と直線の距離公式は,
- 複雑
- よく使う
- 自分でつくるのが困難
という奇跡の三拍子が見事に揃っているからです。
これを文字だけで単純に暗記しても,すぐに忘れてしまいます。
要素ごとに何をやっているのかを細かく見ながら,使えるようにしていきましょう。
点と直線の距離公式を覚える
それでは,点と直線の公式を,絵描き歌風(?)に,順を追って描いていきますよ。
点と直線の距離公式を使うとき,直線の方程式は必ずax+by+c=0の形で使います。
ax+by+c=0の形になっていない場合は,変形してから公式を使いましょう。






順を追って見ていけば,意外と難しくないですよ!ね!(強引)。
実際に使ってみる
公式そのままの問題
具体的な例題で,距離を求めてみましょう。
点(2,3)と直線5x-4y+10=0の距離を求めよ。
例題っていっても,公式に当てはめるだけなのです。
分母のルートの中には,xとyの係数の2乗の和を,分子の絶対値には直線に点を代入したものを書くよ。
解答はこちら。
\cfrac{|5\cdot 2-4\cdot 3+10|}{\sqrt{5^2+(-4)^2}}=\cfrac{8}{\sqrt{41}} …(答)
分母の有理化はしてもしなくてもいいと思います。
円の接線を求めるときに多用します
ただ距離を求めるだけでは嬉しさも少なめです。
実用としては,円の接線を求めるときによく使われます。
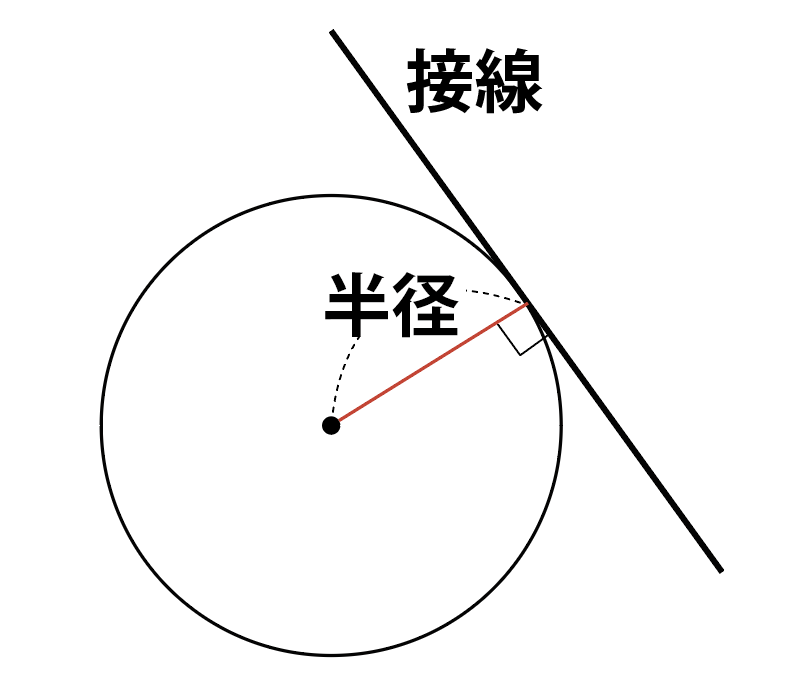
上の図のように,円の中心と接線の距離は,円の半径と同じになることを利用して,円の接線の問題ができます。
具体的な問題は,円の接線の記事で紹介していますので,よかったらどうぞ。

点と直線の距離公式の証明
点と直線の距離公式の証明方法はいくつかありますが,なるべく短く済む方法をやります。
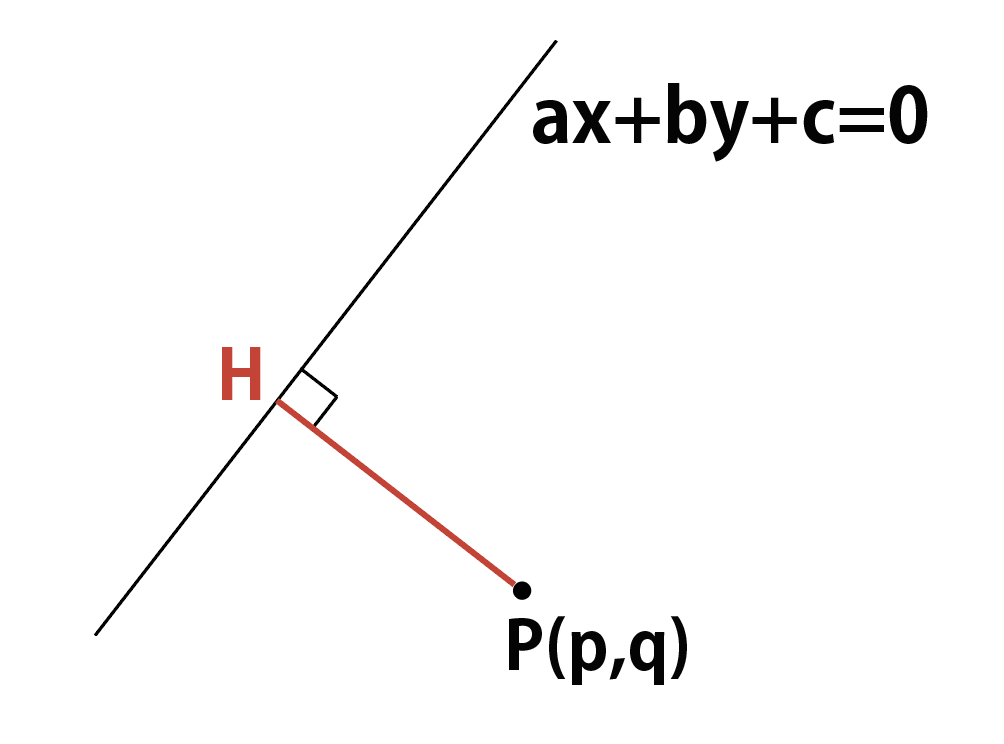
(p,q)をP,Pから直線に下ろした垂線の足をHとしたときのPHの長さが出ればOK。おうちに帰れます。
 粗茶さん
粗茶さん説明の都合上,図の向きが変わりましたが,計算は同じです。
今回の方法の場合,直線の式をy=\cdots の形に変形します。
ax+by+c=0 \Leftrightarrow y=-\cfrac{a}{b}x-\cfrac{c}{b}
この先の計算が煩雑にならないように,一旦,
m=-\cfrac{a}{b},n=-\cfrac{c}{b} …(*)として,
y=mx+n …①
としておきます。
次に,直線x=pを引いて,①との交点をQとします。
さらに,下図のRSが1となるような場所に,①から垂線RSを引きます。

ここでできる2つの三角形は,3角が等しいので,相似です。
(△PQH∽△SQR)
Qはx=pと①の交点なので,x座標はp,y座標は①にx=pを代入してmp+nになります。
PQの長さは,PとQのy座標の差なので,|mp+n-q|

 粗茶さん
粗茶さん図によってはmp+nよりもqのほうが大きい場合もあるので,絶対値をつけておきましょう。
次に,△SRQの辺の長さを求めます。傾きに注目します。
①の傾きはmですが,これはQSの傾きでもあって,
m=\cfrac{\rm RQ}{\rm RS}=\cfrac{\rm RQ}{1}
ということで,{\rm RQ}=m
さらに三平方の定理で,{\rm SQ}=\sqrt{m^2+1^2}

△PQH∽△SQR より,
{\rm PH:SR=PQ:SQ}
⇔{\rm PH}=\cfrac{\rm PQ\cdot SR}{\rm SQ}
=\cfrac{|mp+n-q|\cdot 1}{\sqrt{m^2+1}}
=\cfrac{|mp+n-q|}{\sqrt{m^2+1}}
(*)より,m=-\cfrac{a}{b},n=-\cfrac{c}{b} だったので,これらを代入して,
{\rm PH}=\cfrac{\left|-\cfrac{a}{b}\cdot p-\cfrac{c}{b}-q\right|}{\sqrt{\left(-\cfrac{a}{b}\right)^2+1}}
=\cfrac{\left|\cfrac{a}{b}\cdot p+q+\cfrac{c}{b}\right|}{\sqrt{\cfrac{a^2}{b^2}+1}}
 粗茶さん
粗茶さん絶対値の中身にマイナスをかけても,全体の値は変わりません。
最後に分母と分子をb倍して,
{\rm PH}=\cfrac{|ap+bq+c|}{\sqrt{a^2+b^2}}
できました!!
道のりは長いですが,おそらくこれが計算量が最も少なくてできる方法だと思います。
もし機会があれば,ぜひご採用ください。
点と直線の距離 まとめ
この記事では,点と直線の距離の公式の覚え方と,証明を紹介しました。
点と直線の距離の公式は,基本的に暗記でいくしかありません。
自分で求めるのはかなり困難ですからね。
点と直線の距離の覚え方のポイントをおさらいしておくと,
- 直線の式はax+by+c=0の形
- 分母はルート,分子は絶対値
- 分母にはxとyの係数の2乗の和
- 分子には点を代入したもの
でした。
きちんと言葉で覚えるようにしておくと,忘れにくいですよ!
図形と方程式 おすすめ参考書
安定の坂田先生です。
このブログでは,自分で勉強しているとき,つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や,勉強が楽しくなる文房具も紹介していますので,よろしければご覧ください!




