 学生の方
学生の方「同じものを含む順列」って,普通の順列と何が違うの?
「同じものを含む順列」という言葉を聞いて、頭を抱えたことはありませんか?
実は、この一見複雑に見える問題も、「組合せ」の考え方を使えば簡単に解けるんです。
この記事では、同じものを含む順列の考え方から計算方法、公式の意味と成り立つ理由まで、わかりやすく解説していきます。
- 同じものを含む順列を,組合せで解く方法がわかる
- 同じものを含む順列の公式が成り立つ理由がわかる

粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

「同じものを含む順列」は「組合せ」で考える
「同じものを含む順列」とは,並べようとするものの中に区別がつかないものがある順列のことです。
普通の順列とはまったく異なる解き方になります。
「同じものを含む順列」は,「場所を選ぶ」
例えばこんな問題。
A,A,B,C,D の5文字の並べ方は何通りか。
 学生の方
学生の方5文字だから,5!じゃないの?
階乗や_nP_rを使えるのは,異なる5個のものを並べるときです。
今回は同じもの(A)が2つあるので,普通の順列では並べ方の数を求めることができません。
同じものを含む順列は,なんと「組合せ(_nC_r)を使って計算します。
 学生の方
学生の方組合せって,並べないんじゃなかったっけ?
 粗茶さん
粗茶さん組合せ(C)自体は並べ方を考えないものですが,特殊な順列の場合にも利用しますよ。
_nC_rの計算方法については,別の記事で解説していますので,不安な人は参照してください。

それでは,問題を解いていきましょう。
今回は5つの文字を並べるので,①〜⑤の5つの席を用意して,それぞれの場所に文字を入れていくことを考えます。
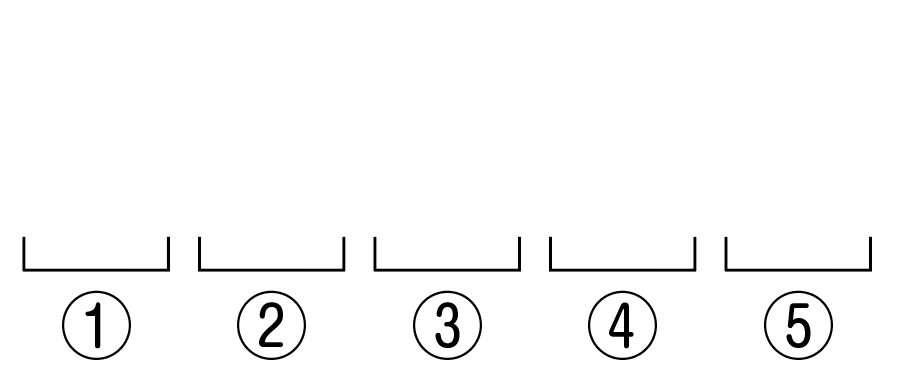
まず,①〜⑤の中から2か所を選んで,2個のAを入れます。
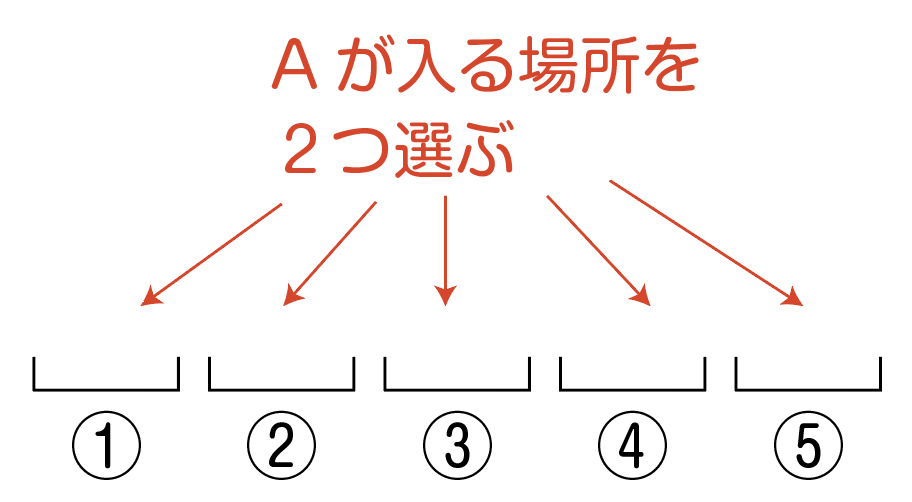
Aが入る場所の選び方は,5か所から2か所を選ぶので,_5C_2通りですね。
例えば,①と③にAが入ったとしましょう。
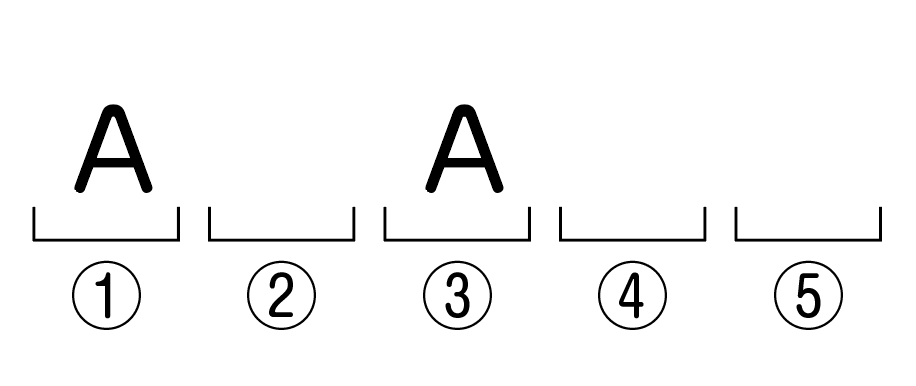
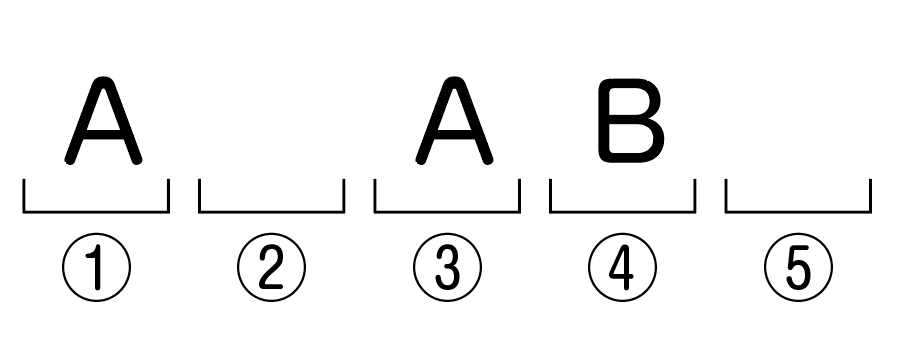
次に,空いている②・④・⑤の3か所から,Bが入る1か所を選びます。
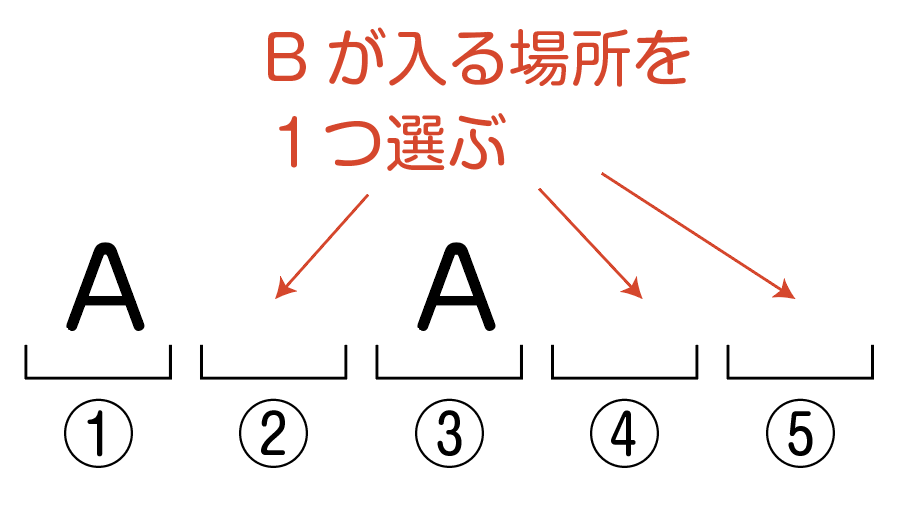
Bが入る場所の選び方は,3か所から1か所を選ぶので,_3C_1通り。
例えば,④にBが入ったとします。
続いて,残っている②・⑤の2か所から,Cが入る1か所を選びます。
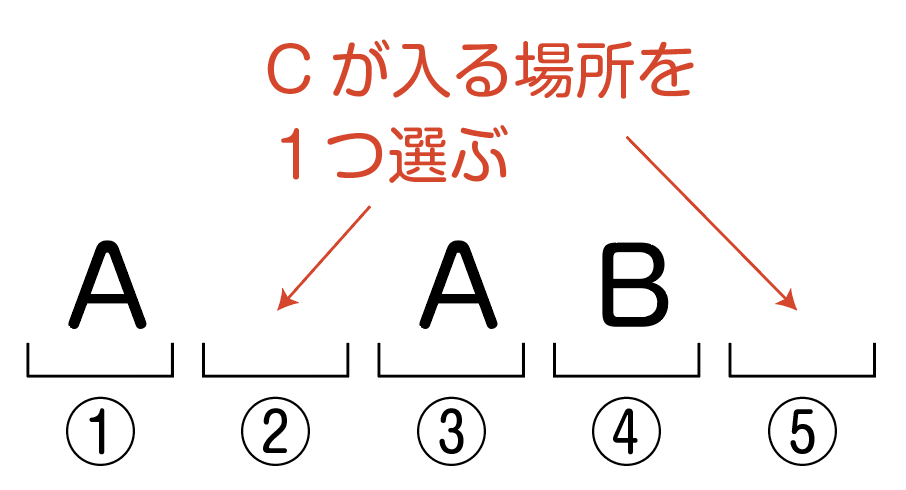
2が入る場所の選び方は,2か所から1か所を選ぶので,_2C_1通り。
例えば⑤にCが入ったとしましょう。
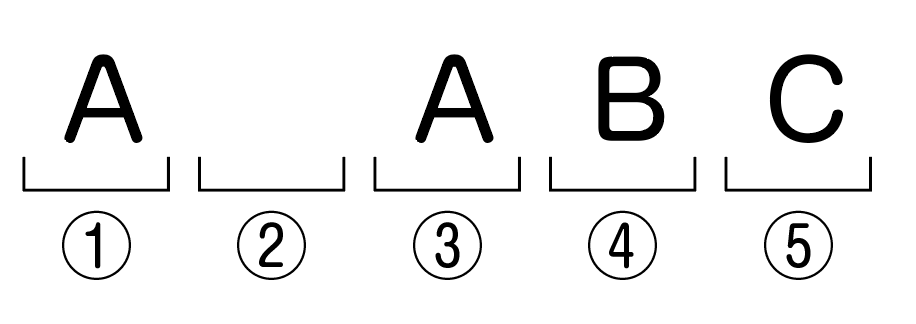
もう②しか残っていないので,自動的に②にDが入って(_1C_1通り)完成。
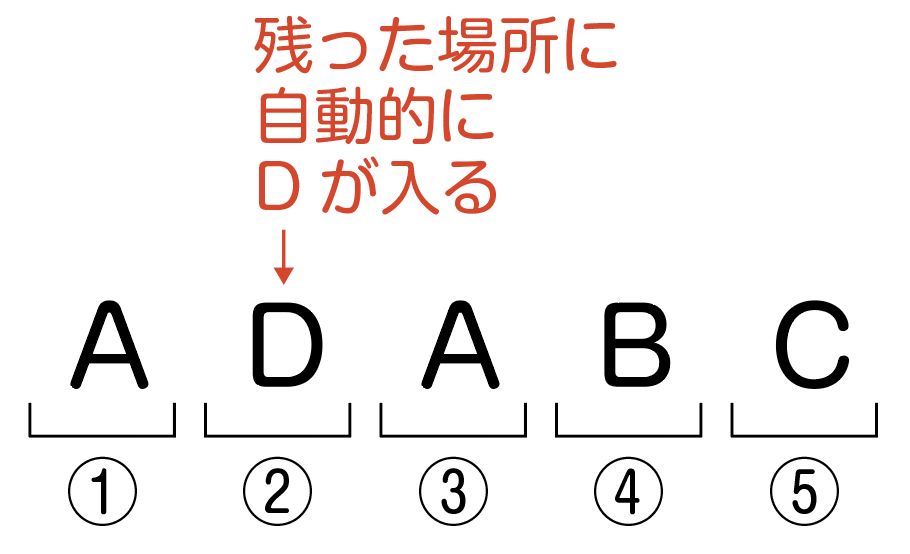
ということで,
Aの入る場所の選び方が_5C_2通り,
それぞれに対してBの入る場所の選び方が_3C_1通り,
それぞれに対してCの入る場所の選び方が_2C_1通り,
それぞれに対してDの入る場所の選び方が_1C_1通りあるので,
 粗茶さん
粗茶さん最後の_1C_1は省くことが多いかな。
求める並べ方は,
_5C_2\times_3C_1\times_2C_1\times_1C_1=10\times3\times2\times1=60(通り)
同じものを含む順列は,
空いている場所から,文字をいれる場所を選ぶ
というアプローチで考えると解きやすくなります。
同じものの種類が増えても考え方は同じ。
例題1では同じ文字がAだけでしたが,複数個ある文字の種類が増えても,同じ考え方でできます。
A,A,B,B,B,C,C,C,D の9文字の並べ方は何通りか。
 学生の方
学生の方同じ文字がめっちゃ増えた。
 粗茶さん
粗茶さん文字の種類が増えても,考え方は同じです。場所を選んでいきましょう。
全部で9文字あるので,場所を9個用意します。
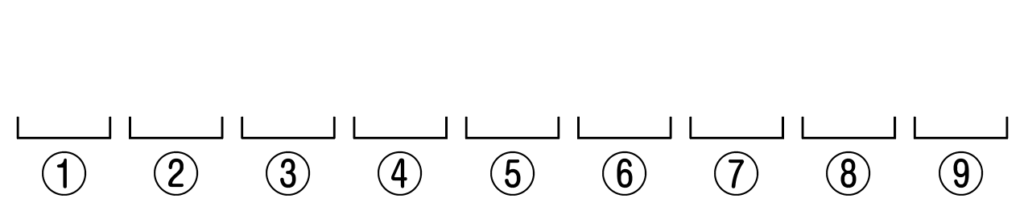
 学生の方
学生の方まずはAが入る場所を考えて…
 粗茶さん
粗茶さんAからでも解けますが,数が少ない文字から入れていったほうが,計算が簡単になりますよ。
 学生の方
学生の方そうなの?じゃあ1文字しかないDからだね。
まず,①〜⑨の中から1か所を選んで,Dを入れます。
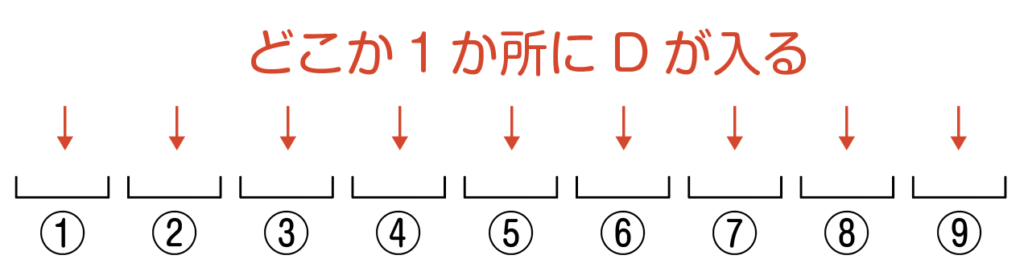
Dが入る場所の選び方は,9か所から1か所を選ぶので,_9C_1通り。
例えば⑤にDが入ったとします。
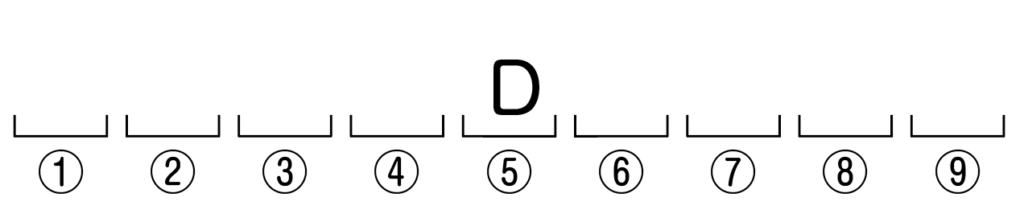
次に,残りの8か所から,Aが入る2か所を選びます。
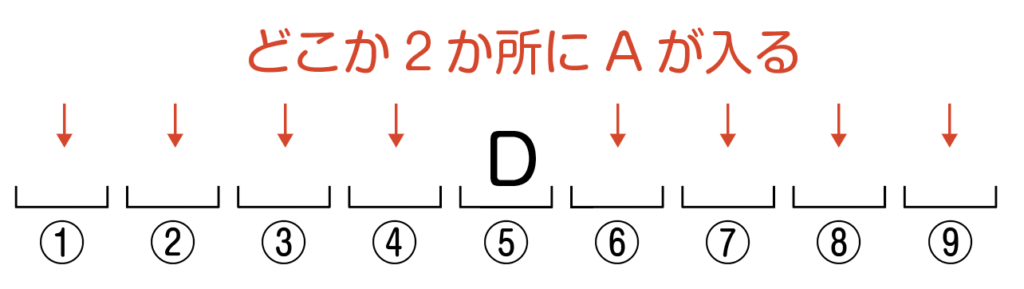
Aが入る場所の選び方は,8か所から2か所を選ぶので,_8C_2通り。
例えば②と⑨にAが入ったとしましょう。

続いて,残り6か所から,Bの入る3か所を選ぶ。
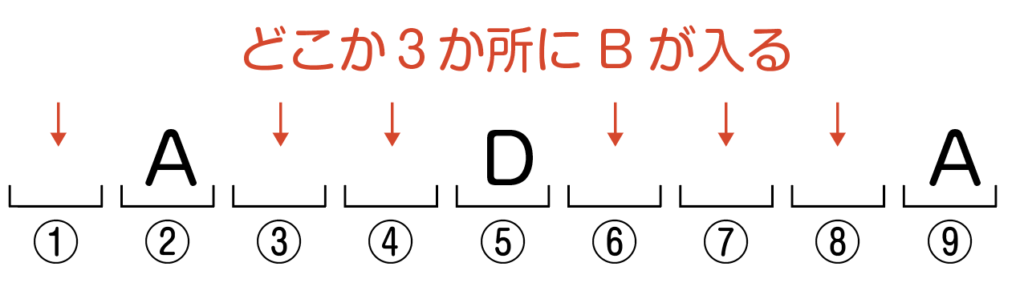
Bが入る場所の選び方は,6か所から3か所を選ぶので,_6C_3通り。
例えば①・③・⑧にBが入ったとします。
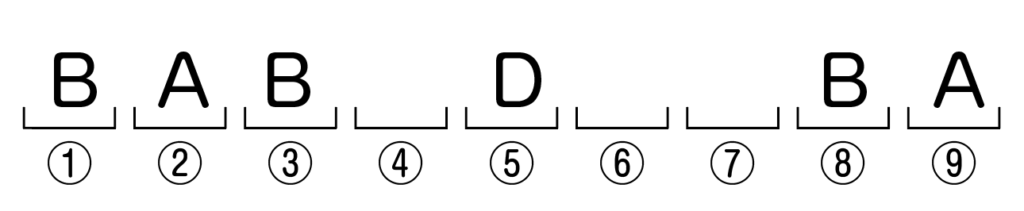
あと3か所残っていますが,あとはCを3ついれるだけなので,空いているところに自動的にCが入る(_3C_3通り)。
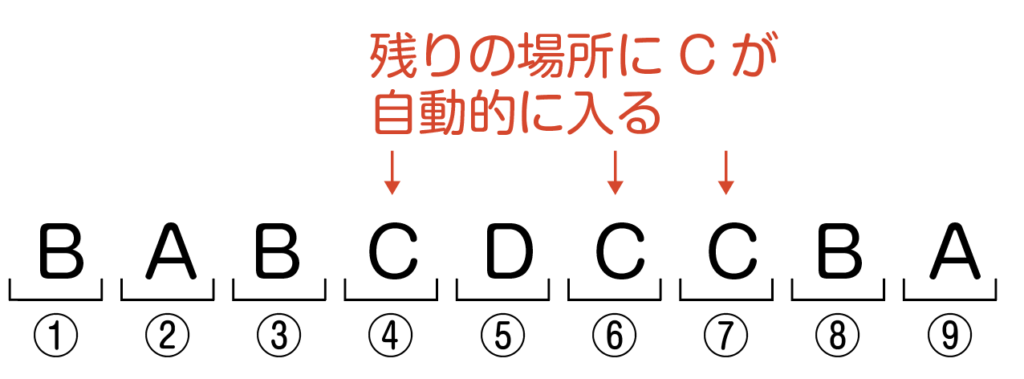
ということで,
Dの入る場所の選び方が_9C_1通り,
それぞれに対して2つのAが入る場所の選び方が_8C_2通り,
それぞれに対して3つのBが入る場所の選び方が_6C_3通り,
それぞれに対して3つのCが入る場所の選び方が_3C_3通りあるので,
 粗茶さん
粗茶さんやはり最後の_3C_3は書かずに,「残り3か所に自動的にCが入る」みたいな記述にするのもOK
求める並べ方は,
_9C_1\times_8C_2\times_6C_3\times_3C_3=9\times28\times20\times1=5040(通り)
重複する文字の種類が増えても,同じ考え方で解くことができます。
「同じものを含む順列」の公式
 学生の方
学生の方同じものを含む順列って,なんか階乗をつかった公式があったような気がするんだけど…
同じものを含む順列には,公式があります。
n個のもののうち,p個,q個,r個,…が同じものであるとき,それらn個のものすべてを1列に並べる順列の総数は,
\cfrac{n!}{p!\cdot q!\cdot r!\cdots}(ただし,p+q+r+\cdots=n)
何のことだかよくわからないと思うので,先ほどの例題2の場合で考えてみると,
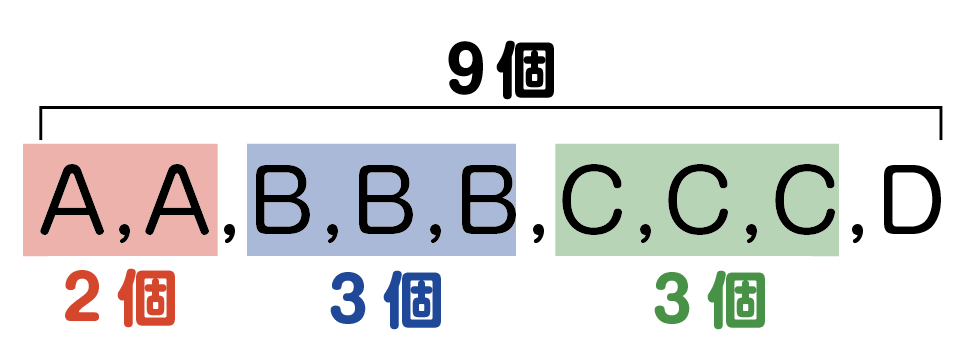
全部で9個あって,Aが2個,Bが3個,Cが3個重複しているので,並べ方は,
\cfrac{9!}{{\color{red}2!}\cdot {\color{blue}3!}\cdot {\color{green}3!}}=\cfrac{9\cdot 8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2}{2\cdot 3\cdot 2\cdot 3\cdot 2}=9\cdot 8\cdot 7\cdot 5\cdot 2=5040(通り)という感じで計算できます。
「同じものの個数の階乗で割る」というイメージです。
 学生の方
学生の方さっきのCを使ってるやり方と全然違うんだけど…
見た目は_nC_rを用いる方法とは違って見えますが,こうするとどうでしょう?
\begin{array}{ll}
&\cfrac{9!}{2!\cdot 3!\cdot 3!}\\\\\\
=&\cfrac{9\cdot 8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2}{2\cdot 3\cdot 2\cdot 3\cdot 2}\\\\\\
=&9\times\cfrac{8\cdot 7}{2}\times\cfrac{6\cdot 5\cdot 4}{3\cdot 2}\times \cfrac{3\cdot 2}{3\cdot 2}
\\\\\\
=&9\times\cfrac{8\cdot 7}{2\cdot 1}\times\cfrac{6\cdot 5\cdot 4}{3\cdot 2\cdot 1}\times \cfrac{3\cdot 2\cdot 1}{3\cdot 2\cdot1}\\\\\\
=&_9C_1\times_8C_2\times_6C_3\times_3C_3
\end{array} 学生の方
学生の方あ,例題2と同じ式になった!
同じ問題をやっているので当たり前ではあるのですが,同じものを含む順列の公式は,実は_nC_rを使った計算と同じことをしているのです。
「同じものを含む順列」の公式が成り立つ理由
「同じものを含む順列」の公式が一般的に成り立つことを示してみます。
その前に,Cの計算方法が一般的に次のように書けることを確認してきましょう。
_nC_r=\cfrac{n!}{(n-r)!r!}具体例を考えるとわかるかと思います。
_8C_3=\cfrac{8!}{5!3!}=\cfrac{8\cdot 7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}{5\cdot 4\cdot 3\cdot 2\cdot 1\cdot 3\cdot 2\cdot 1}=\cfrac{8\cdot 7\cdot 6}{3\cdot 2\cdot 1}それでは示してみます。
n個のもののうち,p個,q個,r個が同じものであるとき,n個のものすべてを1列に並べる順列の総数を考える(ただしp+q+r=n)。
n個の場所から,p個の同じものが入る場所の選び方は,_nC_p通り。
残りn-p個の場所から,q個の同じものが入る場所の選び方は,_{n-p}C_q通り。
残りn-p-q(=r)箇所には,残ったr個が自動的に入る。
よって,求める並べ方は,
\begin{array}{ll}
&_nC_p\times _{n-p}C_q\\\\
=&\cfrac{n!}{(n-p)!p!}\times\cfrac{(n-p)!}{(n-p-q)!q!}\\\\
=&\cfrac{n!}{p!q!(n-p-q)!}\\\\
=&\cfrac{n!}{p!q!r!}
\end{array} 粗茶さん
粗茶さんn=p+q+rより,n-p-q=rです。
公式が成り立つ理由について,並べるものが3種類である場合で説明しましたが,4種類以上になっても同様に成り立ちます。
Cを使うか,公式を使うか
 学生の方
学生の方Cとか使うのめんどくさいから,公式でいい?
確かに公式のほうが考えることが少ないので導入しやすいかもしれません。
ただし,公式は導入しやすい一方,Cを使う場合よりも計算量が多くなる傾向があることには注意しましょう。
また,問題集の解説を読むと,Cを使った方法しか載っていないこともあるので,Cを使った解き方もできるようになっておいたほうが良いですよ。
まとめ
同じものを含む順列は、一見難しく感じるかもしれませんが、「場所を選ぶ」という発想で組合せの考え方を適用することで、効率的に解くことができます。
同じものの個数の階乗で割る公式で解く方法も有効です。
どちらの方法も本質的には同じことを計算していますが、問題の性質に応じて使い分けることで、より効率的に解くことができますよ。
このブログでは,自分で勉強しているとき,つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や,勉強が楽しくなる文房具も紹介していますので,よろしければご覧ください!



