絶対値の外し方，意外と簡単です。基本をしっかりマスターしよう！

学生の方

絶対値が出てくると，やる気なくすわー。

絶対値の外し方で悩んでいませんか？

中学校では「符号を取り除く」だけで終わっていた絶対値。

高校では単純な計算問題だけでなく，方程式・不等式や関数，積分など，様々な分野に出現します。

この記事では，絶対値の意味から基本的な外し方，絶対値の中に文字が含まれる場合の計算のしかたをわかりやすく説明します。

絶対値の方程式・不等式については，以下の記事で解説しています。

あわせて読みたい

絶対値を含む方程式・不等式は怖くない！解き方の「形」を身につけよう。 方程式や不等式に絶対値が入っていると，突然難しくなるよね… 絶対値を含む方程式・不等式の解き方で悩んでいませんか？ 実は，絶対値の方程式・不等式は，やり方を覚え…

この記事を書いた人

粗茶

• 文系に特化して数学を分かりやすく教える高校数学の専門家
• 指導歴14年
• 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

数学の問題集の進め方について、noteでも発信しています。よろしければご覧ください！

絶対値とは

絶対値は「距離」

「xの絶対値」とは「数直線上で0からxまでの距離」のことです。

例えば「2の絶対値」は，「数直線上で0から2までの距離」なので，2です。

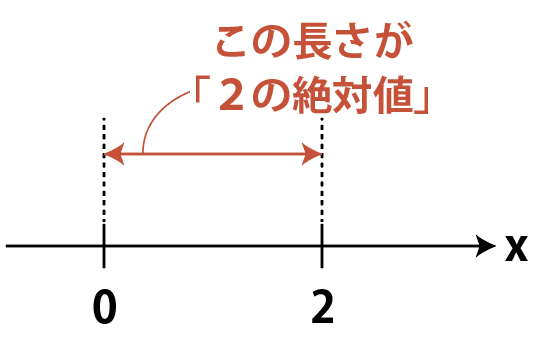
「−2の絶対値」は「数直線上で0から−2までの距離」なので，やっぱり2です。

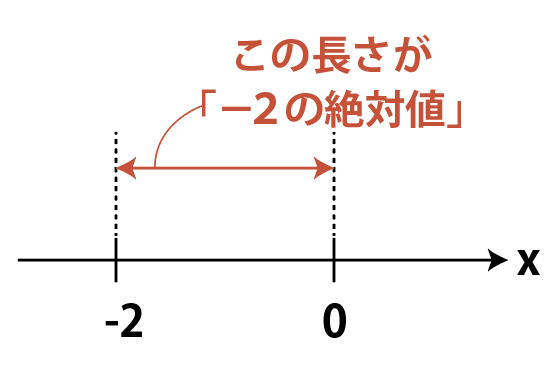
絶対値は必ず0以上になることを覚えておきましょう。

絶対値は「距離（長さ）」なので，マイナスになることは絶対にありません。

絶対値の記号

中学校の数学では「２の絶対値」のように，「絶対値」という言葉で表現していました。

しかし，高校では，記号を使って絶対値を表現します。

絶対値の定義と記号

数直前上で原点（0）から，ある実数aまでの距離を「aの絶対値」といい，

\LARGE{|a|}

と書く。

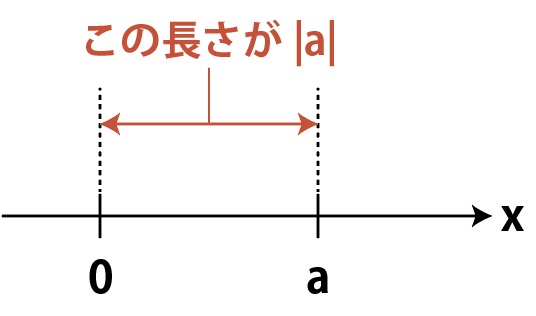
数を縦棒で挟むと，絶対値になります。例えば，

「2の絶対値」は|2|，

「-2の絶対値」は|-2|

のように書きます。

絶対値の基本的な外し方

絶対値の外し方は，中身が0以上の場合と負の場合で変わります。

一般的には次のようになります。

|a|=\begin{aligned}
\left\{
\begin{array}{l}
a&(a\geqq 0のとき)\\\\
-a&(a<0のとき)
\end{array}
\right.
\end{aligned}

絶対値の中身が0以上の場合は，絶対値があってもなくても変わらないので，そのまま絶対値の記号を消せばOK。

一方，絶対の中身が負の場合は，マイナスを消す（符号を変える）工程が必要になります。

マイナスを消すためには，マイナスをかける（−１倍する）という操作が入ります。

粗茶さん

マイナスかけるマイナスはプラスですからね。

つまり，絶対値の中身の数字が0以上か負かを判断して，0以上ならばそのまま絶対値記号を消し，負ならば中身の数字にマイナスをかけて絶対値記号を消します。

例題をやってみましょう。

（1）中身が正の数なので，そのまま絶対値記号を外せばOK。

|4|=4　\cdots(答)

（2）中身が負の数なので，マイナスをかけてから絶対値記号を外します。

\left|-\cfrac{2}{3}\right|=-\left(-\cfrac{2}{3}\right)=-\cfrac{2}{3}　\cdots(答)

粗茶さん

最終的な値が0以上になっていることを確認しましょう。絶対値は必ず0以上だからね。

（3）中身が式になっているときは，中身の式を計算したあとに，符号を調べる。

|1-4.3|=|-3.3|=-(-3.3)=3.3　\cdots(答)

（4）絶対値の中に絶対値が入っているときは，内側から外す。

\begin{aligned}
&　|2-\color{red}|-3|\color{black}|\\\\
&=|2-\color{red}\{-(-3)\}\color{black}|\\\\
&=|2-{\color{red} 3}|\\\\
&=|-1|\\\\
&=-(-1)\\\\
&=1　\cdots(答)
\end{aligned}

粗茶さん

今回は丁寧に|-3|=-(-3)=3って書きましたが，
中身が数字だけのときは，すぐに|-3|=3って書いてもOK。

（5）\pi=3.14\cdotsなので，\pi-4は負。よってマイナスをつけてはずすことに。

|\pi-4|=-(\pi-4)=4-\pi　\cdots(答)

このように，絶対値の中身の符号を確認して，0以上ならそのまま，負ならマイナスをつけて外すことを徹底させましょう。

場合分けが必要な絶対値の外し方

絶対値の中身に文字を含む式がはいっているときは，場合分けの形で表すことになります。

学生の方

場合分け，苦手なんだよね…

粗茶さん

公式に当てはめるだけなので，そんなに難しく考えなくても大丈夫！

絶対値記号が１つの場合の外し方

まずは絶対値記号が式の中に１つだけある場合です。

学生の方

x-1の符号がわからないよ…

粗茶さん

わからないときは，場合分けですよ！

場合分けのときは，最初の公式を思い出してください。

|a|=\begin{aligned}
\left\{
\begin{array}{l}
a&(a\geqq 0のとき)\\\\
-a&(a<0のとき)
\end{array}
\right.
\end{aligned}

このaのかわりに，x-1を当てはめれば，場合分けはできあがりです。

単純にあてはめると

|x-1|=\begin{aligned}
\left\{
\begin{array}{l}
x-1&({\color{red}x-1\geqq 0}のとき)\\\\
-(x-1)&({\color{red}x-1<0}のとき)
\end{array}
\right.
\end{aligned}

これでも悪くないのですが，xの条件（赤い部分）は，なるべく簡単にしたほうがいいので，赤い部分の不等式を解いて，

|x-1|=\begin{aligned}
\left\{
\begin{array}{l}
x-1&({\color{red}x\geqq 1}のとき)\\\\
-x+1&({\color{red}x<1}のとき)
\end{array}
\right.
\cdots(答)
\end{aligned}

粗茶さん

ついでに-(x-1)も展開しておきました。

とりあえず公式に当てはめてから，式を簡単に直していけば，意外と簡単に場合分けできます。

もう少し例題で確認してみましょう。

（1）分数式ですが，やりかたは同じです。

\begin{aligned}\left|\cfrac{1}{3}x-1\right|&=
\left\{
\begin{array}{l}
\cfrac{1}{3}x-1&\left(\cfrac{1}{3}x-1\geqq 0のとき\right)\\\\
-\left(\cfrac{1}{3}x-1\right)&\left(\cfrac{1}{3}x-1<0のとき\right)
\end{array}
\right.\\\\&=
\left\{
\begin{array}{l}
\cfrac{1}{3}x-1&(x\geqq 3のとき)\\\\
-\cfrac{1}{3}x+1&(x<3のとき)
\end{array}
\right.　…(答)
\end{aligned}

（2）xの係数がマイナスなので，不等号の向きに注意しましょう。

\begin{aligned}|3-2x|&=
\left\{
\begin{array}{l}
3-2x&(3-2x\geqq 0のとき)\\\\
-(3-2x)&(3-2x<0のとき)
\end{array}
\right.\\\\&=
\left\{
\begin{array}{l}
3-2x&\left(x\leqq\cfrac{3}{2}のとき\right)\\\\
-3+2x&\left(x>\cfrac{3}{2}のとき\right)
\end{array}
\right.　…(答)
\end{aligned}

（3）2次式は，場合分けの式が2次不等式になります。

\begin{aligned}|x^2-3x+2|&=
\left\{
\begin{array}{l}
x^2-3x+2&(x^2-3x+2\geqq 0のとき)\\\\
-(x^2-3x+2)&(x^2-3x+2<0のとき)
\end{array}
\right.\\\\&=
\left\{
\begin{array}{l}
x^2-3x+2&(x\leqq 1，2\leqq xのとき)\\\\
-x^2+3x-2&(1<x<2のとき)
\end{array}
\right.　…(答)
\end{aligned}

絶対値が複数あるときは，１つずつ場合分けする

１つの式に絶対値記号が２つ以上あるときは，手間が増えます。

学生の方

これは厳しいなあ…

粗茶さん

2つの絶対値を同時に考えることは難しいので，１つずつ場合分けしましょう。

少し長いので，順を追って説明します。

STEP

１つずつの絶対値を場合分けする

2つの絶対値を，それぞれ場合分けします。

公式に当てはめればOK。

|x+3|=\begin{aligned}
\left\{
\begin{array}{l}
x+3&(x\geqq -3のとき)\\\\
-x-3&(x<-3のとき)
\end{array}
\right.
\end{aligned}

|x-1|=\begin{aligned}
\left\{
\begin{array}{l}
x-1&(x\geqq 1のとき)\\\\
-x+1&(x<1のとき)
\end{array}
\right.
\end{aligned}

STEP

それぞれの場合分けの範囲を値を図にする

|x+3|は，xが-3以上ならx+3，xが-3より小さければ-x-3なので，

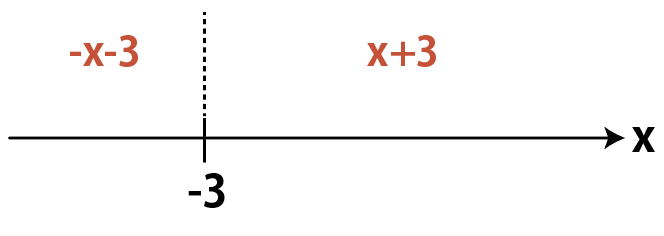
というイメージ。同じようにして，

|x-1|は，xが1以上ならx-1，xが1より小さければ-x+1なので，

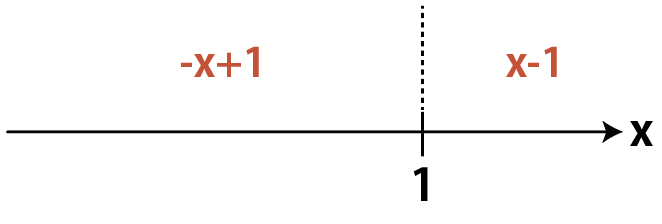
と表すことができます。

STEP

2つの範囲を合体する

STEP2で作った図を合体させると，場合分けが完成。

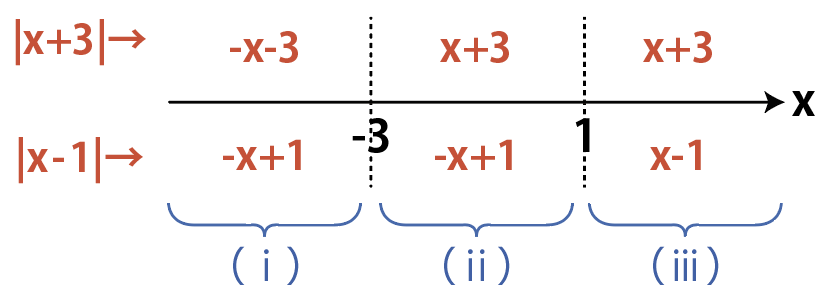
図を見ながら場合分けしていきます。

\begin{aligned}
({\rm i})&x<-3のとき\\\\
&|x+3|=-x-3，|x-1|=-x+1　なので，\\\\
&|x+3|+|x-1|=-x-3+(-x+1)=-2x-2\\\\\\\\
({\rm ii})&-3\leqq x<1のとき\\\\
&|x+3|=x+3，|x-1|=-x+1　なので，\\\\
&|x+3|+|x-1|=x+3+(-x+1)=4\\\\\\\\
({\rm iii})&1\leqq xのとき\\\\
&|x+3|=x+3，|x-1|=x-1　なので，\\\\
&|x+3|+|x-1|=x+3+(x-1)=2x+2
\end{aligned}

以上をまとめて，

|x+3|+|x-1|=\begin{aligned}
\left\{
\begin{array}{ll}
-2x-2&(x<-3のとき)\\\\
4&(3\leqq x<1のとき)\\\\
2x+2&(1\leqq xのとき)
\end{array}
\right.
\end{aligned}　\cdots (答)

絶対値が複数ある場合は，図に表して場合分けを考えることで，ミスを減らせます。

絶対値の外し方をしっかりマスターしよう

この記事では，絶対値の意味から基本的な外し方，絶対値の中に文字が含まれる場合の計算のしかたを説明しました。

一見難しそうに見える絶対値ですが，基本をしっかりおさえれば，怖くありません。

絶対値はさまざまな単元で扱われていきます。

応用問題にも対応できるように，絶対値の基本的な外し方をしっかりマスターしておきましょう！

絶対値の外し方をマスターしたら，方程式・不等式の問題にも挑戦してみてください。

あわせて読みたい

絶対値を含む方程式・不等式は怖くない！解き方の「形」を身につけよう。 方程式や不等式に絶対値が入っていると，突然難しくなるよね… 絶対値を含む方程式・不等式の解き方で悩んでいませんか？ 実は，絶対値の方程式・不等式は，やり方を覚え…

　

このブログでは，自分で勉強しているとき，つまづきやすいポイントを解説。

「かゆいところに手が届く」情報を発信しています。

自分で勉強する際にオススメの参考書や，勉強が楽しくなる文房具も紹介していますので，よろしければご覧ください！

あわせて読みたい

製図用シャープで楽しく勉強！ノートがパッと華やぐ！ ノートが汚くて自分でも読めないときがあるんだよね。 「製図用シャープ」があなたのノートのお悩みを解決します。 製図用シャープは、ただの筆記具ではありません。 あ…

あわせて読みたい

【高校生】数学が全くわからないあなたへ！自分で勉強できるおすすめ参考書ガイド 数学の先生が変わって， 先生が何言ってるか全然わからない。ピンチ… という状況で悩んでいませんか？ 私も高校生の時，そうでした。 高１のときの先生はよかったけど，…