 学生の方
学生の方素因数分解をすることがあるけど,2で割って,3で割って…って,何回も割り算するのが大変。
整数の問題などで登場する素因数分解。
一般的には,素因数分解したい数を2から順に素数で割っていき,割れなくなるまで割り続けるという方法を習います。
もちろん確実に素因数分解ができるわけですが,大きい数を素因数分解する場合に時間がかかるし,スペースも多く取ってしまいます。
そこでこの記事では,素因数分解をなるべく早く,場所を取らずに,スマートに解く方法を紹介します。
- 素因数分解を素早く,スマートにできるようになる。

粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

素数とは1と自身以外で割り切れない数
素因数分解の前に,その主役である素数とは何か説明しておきます。
素数とは,1とそれ自身以外で割り切れない整数のことです。
例えば,5は,1と5以外では割り切れないので,素数です。
一方,6は,1と6以外に,2と3でも割り切れるので,素数ではありません(ちなみに,素数でない数を「合成数」といいます)
また,1は素数ではないことも決まっているので,最も小さい素数は2です。
素数についてはわかっていないことが多くて,いくつあるのかもはっきりしません。
 粗茶さん
粗茶さん現時点で発見されている最大の素数は2000万桁以上あるものだそうです。
ちなみに100以下の素数は25個あります。
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97
素因数分解とは,素数の積で表すこと
ある数を素数の積の形で表すことを素因数分解といいます。
例えば12は2×2×3なので,
12=2^2\times 3
39000は2×2×2×3×5×5×5×13なので,
39000=2^3\times 3\times 5^3\times 13
のように表すことができます。
素因数分解の方法①:順に素数で割る(一般的な方法)
素因数分解の一般的な方法は,2から順に素数で割っていく方法です。
例えば,12を素因数分解してみます。
12を2で割って,6。
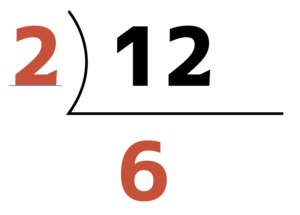
6を2でわって,3。
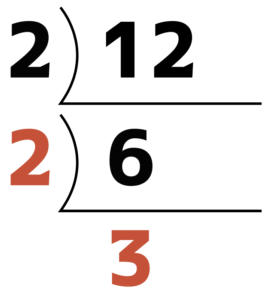
3は2で割れないので,3で割って,1。
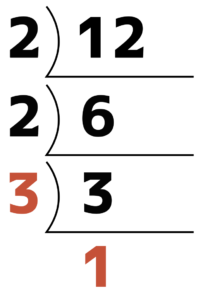
1になったら終わりで,割る数をならべて完了。
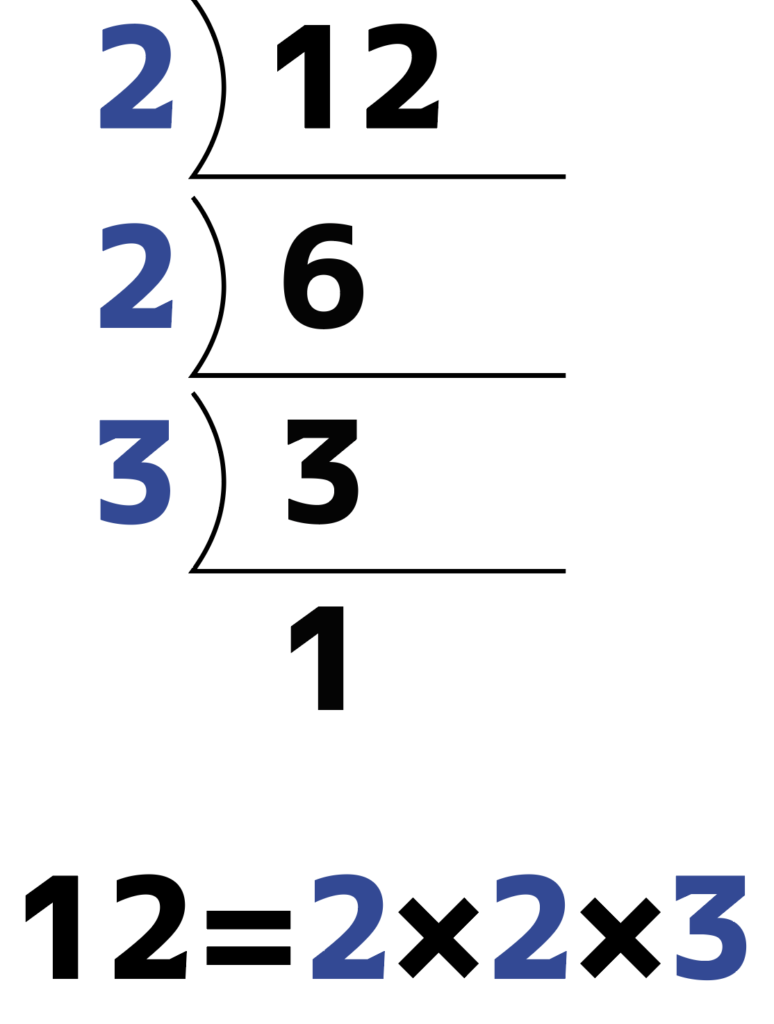
この方法でまったく問題はないのですが,大きい数を扱う際にはとても長くなります。
たとえば39000を素因数分解すると,筆算がかなりの縦長になります。
素因数分解が機械的にできるというところはメリットなのですが,何回も割り算をしなきゃならないし,場所も取るというデメリットもあります。

素因数分解の方法②:とにかく積の形にできればOK
素因数分解を中学校で習うとき,必ず①の「2から順に割っていく」方法をやるので,2から順に1つずつ割っていかなければならないと思っている人が多いように思います。
ですが,素因数分解の目的は,あくまで素数の積で表すことですので,2から順になっている必要はありません。
大まかに分けて,それぞれを細かくしていく
39000の例で説明しましょう。
まず,明らかに1000の倍数なので,39と1000に分けることが可能。
39000=39\times 1000
そして39は3の倍数,1000は10の3乗なので,
39\times 1000=3\times 13\times 10^3
だいぶ細かくなりました。あと素数じゃないのは10だけです。10は2×5なので,
3\times 13\times 10^3=3\times 13\times (2\times 5)^3
これですべてが素数になったので,整理して,答えは,
39000=\color{red}2^3\times 3\times 5^3\times 13いかがでしょうか?筆算をするよりは,かなりスマートに,速く求めることができています。
倍数の判定法を利用して,割る数を見つけよう
一見,何で割ればいいかわかりづらい数のときは,倍数の判定法を使うと,割る数を見つけやすいです。
倍数の判定法については,こちらの記事でまとめています。

4158を素因数分解しなさい。
初手でのおすすめは,各位の数字を足してみることです。
各位の数の和から,3の倍数と9の倍数が判定できます。
- 各位の和が3の倍数→もとの数は3の倍数
- 各位の和が9の倍数→もとの数は9の倍数
 粗茶さん
粗茶さん3の倍数と9の倍数しか判定できませんので,そこはご注意を…
素因数分解を求められる数は,たいてい3を素因数に持っているので,3とか9(=3×3)で割り切れることが多いです。
実際,今回の4158について,各位の数字を足すと,4+1+5+8=18で,9の倍数になります。
よって,4158は9の倍数だということがわかります。
そこで,4158を9で割ってみます。
4158=9\times 462
次に,462についても各位の数字を足すと,4+6+2=12で,3の倍数です。
さらに462は偶数(2の倍数)でもあるので,3×2=6の倍数ということがわかります。
そこで,462を6で割ってみますと,続きはこうなります。
4158=9\times 462=9\times 6\times 77
ここまでくれば,あとは自力で分けることができるかと思います。
9は3×3,6は2×3,77は7×11なので,
4158=9\times 462=9\times 6\times 77=3\times 3\times 2\times 3\times 7\times 11=\color{red}2\times 3^3\times 7\times 11このようにして,2から順に割っていく方法よりもスマートに速く素因数分解の計算ができます。
割る順番は決まっていないので,自分が思いついた数で割っていけばよいですよ。
 粗茶さん
粗茶さんうまく割れる数が思いつかないときは,通常の2から順に割っていく方法にするのもアリです。
結果があっていれば,やりかたは自由
今回は,素因数分解をスマートに素早く計算する方法を紹介しました。
最終的に素数の積の形が作れていればよいので,中学校で習った通りの方法でなくてもOKだということを学んでいただければ幸いです。
素因数分解に限らず,計算については,答えがあっていれば,やり方は何でも良いというケースがあります。
自分のやりやすい方法や,効率のよい方法を探してみるのも,数学の実力アップの一助になりますよ。
このブログでは,自分で勉強しているとき,つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や,勉強が楽しくなる文房具も紹介していますので,よろしければご覧ください!



