学生の方
学生の方三角関数の公式って多すぎることない?
三角関数の公式が多くて覚えられない…と悩んでいませんか?
実は,三角関数で,絶対暗記しなきゃいけない公式は少ししかありません。
なぜなら,三角関数のほとんどは,加法定理から自分で作ることができるからです。
この記事では,三角関数で登場する公式を一覧で紹介するとともに,暗記するべきものと自分で作るべきものの区別,そして,加法定理を用いて自分で公式を作る方法を説明します。
この記事を読むと,三角関数の重要事項が効率よく身につき,三角関数の学習に対するハードルが下がること間違いなし!
・三角関数の公式のうち、暗記すべきものと自分で作れるべきものがわかる
・自力で作れるべき公式の作り方がわかる
・それぞれの公式の使いどころがわかる
それでは、さっそくまいりましょう。

粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

三角関数の公式一覧
数Ⅱの三角関数で登場する公式を一覧でまとめていきます。
\begin{array}{l}
① \sin^2\theta+\cos^2\theta=1\\\\
② \cfrac{\sin\theta}{\cos\theta}=\tan\theta\\\\
③ 1+\tan^2\theta=\cfrac{1}{\cos^2\theta}
\end{array}\begin{array}{l}
・\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\\\\
・\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta\\\\
・\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\\\\
・\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\\\\
・\tan(\alpha+\beta)=\cfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\\\\
・\tan(\alpha-\beta)=\cfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}
\end{array}\begin{array}{l}
・\sin2\theta=2\sin\theta\cos\theta\\\\
・\cos2\theta=\cos^2\theta-\sin^2\theta=1-2\sin^2\theta=2\cos^2\theta-1\\\\
・\tan2\theta=\cfrac{2\tan\theta}{1-\tan^2\theta}
\end{array}\begin{array}{l}
・\sin^2\theta=\cfrac{1-\cos2\theta}{2}\\\\
・\cos^2\theta=\cfrac{1+\cos2\theta}{2}\\\\
・\tan^2\theta=\cfrac{1-\cos2\theta}{1+\cos2\theta}
\end{array}\begin{array}{l}
・\sin3\theta=3\sin\theta-4\sin^3\theta\\\\
・\cos3\theta=4\cos^3\theta-3\cos3\theta
\end{array}\begin{array}{l}
・\sin A+\sin B=2\sin\cfrac{A+B}{2}\cos\cfrac{A-B}{2}\\\\
・\sin A-\sin B=2\cos\cfrac{A+B}{2}\sin\cfrac{A-B}{2}\\\\
・\cos A+\cos B=2\cos\cfrac{A+B}{2}\cos\cfrac{A-B}{2}\\\\
・\cos A-\cos B=2\sin\cfrac{A+B}{2}\sin\cfrac{A-B}{2}
\end{array}\begin{array}{ll}
・\sin\alpha\cos\beta=\cfrac{1}{2}\{\sin(\alpha+\beta)+\sin(\alpha-\beta)\}\\\\
・\cos\alpha\sin\beta=\cfrac{1}{2}\{\sin(\alpha+\beta)-\sin(\alpha-\beta)\}\\\\
・\cos\alpha\cos\beta=\cfrac{1}{2}\{\cos(\alpha+\beta)+\cos(\alpha-\beta)\}\\\\
・\sin\alpha\sin\beta=-\cfrac{1}{2}\{\cos(\alpha+\beta)-\cos(\alpha-\beta)\}
\end{array}必ず暗記する三角関数の公式は2つ
まずは、とりあえず暗記しないとはじまらない公式です。
三角関数の相互関係と加法定理の2つは、必ず覚えましょう。
三角関数の相互関係
sinθ、cosθ、tanθのうち、一部しかわかっていないときに、残りを求めるための公式です。
三角関数の定義に近い部分なので、覚えるしかないです。
\begin{array}{l}
① \sin^2\theta+\cos^2\theta=1\\\\
② \cfrac{\sin\theta}{\cos\theta}=\tan\theta\\\\
③ 1+\tan^2\theta=\cfrac{1}{\cos^2\theta}
\end{array}③は忘れてしまっても、①②の組み合わせで求められます。
①:\sin^2\theta+\cos^2\theta=1の両辺を\cos^2\thetaで割って,
\cfrac{\sin^2\theta}{\cos^2\theta}+\cfrac{\cos^2\theta}{\cos^2\theta}=\cfrac{1}{\cos^2\theta}②より,\cfrac{\sin\theta}{\cos\theta}=\tan\theta,つまり\cfrac{\sin^2\theta}{\cos^2\theta}=\tan^2\thetaなので,
\tan^2\theta+1=\cfrac{1}{\cos^2\theta}加法定理
2つ目は加法定理です。
2つの角度の和の三角関数を計算できます。
例えば\sin75^{\circ}の値は知りませんが、\sin(30^{\circ}+45^{\circ})と考えることで、値を求めることができます。
長いですが、この先に出てくるさまざまな公式を作る上で必要なので、これだけはしっかり覚えましょう。
\begin{array}{l}
・\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\\\\
・\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta\\\\
・\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\\\\
・\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\\\\
・\tan(\alpha+\beta)=\cfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\\\\
・\tan(\alpha-\beta)=\cfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}
\end{array}さらに加法定理は、右辺の形を見たときに、左辺へ戻せるようになる必要もあります。
これを象徴するような問題が、2015年度のセンター試験に出題されました。
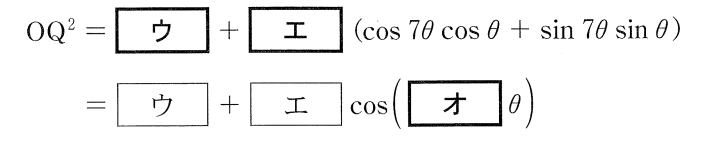
問題の箇所は[ オ ]の部分です。
「は?7倍角?」ということではなく、\cos7\theta\cos\theta+\sin7\theta\sin\thetaがcosの加法定理の右辺の形になっていることに気づかなければなりません。
\cos7\theta\cos\theta+\sin7\theta\sin\theta=\cos(7\theta-\theta)=\cos6\theta
よって,[ オ ]には6が入る。
ということで、加法定理の右辺の形をしっかり覚えていた人は簡単に解けた問題だったんですね。
加法定理を右辺から左辺に変形することは、後にでてくる合成と関係があります。
暗記でもいいが、自分で作れた方がいい三角関数の公式
次に、暗記してもいいですが、自分で作れたほうがいい公式です。
2倍角、半角、3倍角、合成の4つがあります。
2倍角の公式
2倍角の公式は、2θの三角関数をθの三角関数で表す式です。
\begin{array}{l}
・\sin2\theta=2\sin\theta\cos\theta\\\\
・\cos2\theta=\cos^2\theta-\sin^2\theta=1-2\sin^2\theta=2\cos^2\theta-1\\\\
・\tan2\theta=\cfrac{2\tan\theta}{1-\tan^2\theta}
\end{array}これらは、加法定理(α+βの方)のαとβを両方同じにすると作れます。
まずはsinから。
\begin{array}{ll}
&\sin2\theta\\\\
=&\sin(\theta+\theta)\\\\
=&\sin\theta\cos\theta+\cos\theta\sin\theta\\\\
=&2\sin\theta\cos\theta
\end{array}cosも同様にできます。
\begin{array}{ll}
&\cos2\theta\\\\
=&\cos(\theta+\theta)\\\\
=&\cos\theta\cos\theta-\sin\theta\sin\theta\\\\
=&\cos^2\theta-\sin^2\theta
\end{array}cosの2倍角は,相互関係の公式を使ってsinかcosのどちらかに統一した形のほうがよく使われます。
\cos2\theta=\cos^2\theta-\sin^2\thetaに,\cos^2\theta=1-\sin^2\thetaを代入して,
\cos2\theta=(1-\sin^2\theta)-\sin^2\theta=1-2\sin^2\theta
\cos2\theta=\cos^2\theta-\sin^2\thetaに,\sin^2\theta=1-\cos^2\thetaを代入して,
\cos2\theta=\cos^2\theta-(1-\cos^2\theta)=2\cos^2\theta-1
tanもあります。あまり使わないですが。
\tan2\theta=\cfrac{\tan\theta+\tan\theta}{1-\tan\theta\tan\theta}=\cfrac{2\tan\theta}{1-\tan^2\theta}半角の公式
半角の公式は、θの三角関数をを2θの三角関数で表す式です。
\begin{array}{l}
・\sin^2\theta=\cfrac{1-\cos2\theta}{2}\\\\
・\cos^2\theta=\cfrac{1+\cos2\theta}{2}\\\\
・\tan^2\theta=\cfrac{1-\cos2\theta}{1+\cos2\theta}
\end{array}難しそうですが、cosの2倍角の公式を移項すれば作れます。
\begin{array}{ll}
&\cos2\theta=1-2\sin^2\theta\\\\
\Leftrightarrow&\sin^2\theta=\cfrac{1-\cos2\theta}{2}
\end{array}cosも同様に。
\begin{array}{ll}
&\cos2\theta=2\cos^2-1\\\\
\Leftrightarrow &\cos^2\theta=\cfrac{1+\cos2\theta}{2}
\end{array}tanは三角関数の相互関係の公式から求めます。
\tan^2\theta=\cfrac{\sin^2\theta}{\cos^2\theta}=\cfrac{\cfrac{1-\sin2\theta}{2}}{\cfrac{1+\cos2\theta}{2}}=\cfrac{1-\sin2\theta}{1+\cos2\theta}3倍角の公式
3倍角の公式は、3θの三角関数をθの三角関数で表す式です。
\begin{array}{l}
・\sin3\theta=3\sin\theta-4\sin^3\theta\\\\
・\cos3\theta=4\cos^3\theta-3\cos3\theta
\end{array}3θを2θ+θとみなして、加法定理で計算すれば出せます。
\begin{array}{ll}
&\sin3\theta=\sin(2\theta+\theta)\\\\
=&\sin2\theta\cos\theta+\cos2\theta\sin\theta ←加法定理\\\\
=&2\sin\theta\cos\theta\cos\theta+(1-2\sin^2\theta)\sin\theta ←2倍角\\\\
=&2\sin\theta\cos^2\theta+\sin\theta-2\sin^3\theta\\\\
=&2\sin\theta(1-\sin^2\theta)+\sin\theta-2\sin^3\theta ←相互関係\\\\
=&3\sin\theta-4\sin^3\theta ←整理して完成
\end{array}\begin{array}{ll}
&\cos3\theta=\cos(2\theta+\theta)\\\\
=&\cos2\theta\cos\theta-\sin2\theta\sin\theta ←加法定理\\\\
=&(2\cos^2\theta-1)\cos\theta-2sin\theta\cos\theta\sin\theta ←2倍角\\\\
=&2\cos^3\theta-\cos\theta-2\sin^2\theta\cos\theta\\\\
=&2\cos^3\theta-\cos\theta-2(1-\cos^2\theta)\cos\theta ←相互関係\\\\
=&4\cos^3\theta-3\cos\theta ←整理して完成
\end{array}これに関しては自分で作るのにやや時間がかかるので、暗記してもいいと思います。
三角関数の合成
三角関数の合成は、sinθとcosθの和(差)の形を、sin(またはcos)だけにすることをいいます。
実は合成というのは、加法定理の逆変形のことなんです。
公式は覚えなくてよいですが,やりかたは覚えましょう。
\sin\theta+\sqrt{3}\cos\thetaを,r\sin(\theta+\alpha)の形にしなさい。
まず,sinの係数1と,cosの係数\sqrt{3}を2乗して足してルートをつけた\sqrt{1^2+(\sqrt{3})^2}=2で全体をくくります。
\sin\theta+\sqrt{3}\cos\theta=2\left(\sin\theta\cdot\cfrac{1}{2}+\cos\theta\cdot\cfrac{1}{2}\right)次に,sinについている数字\cfrac{1}{2}がcosに,cosについている数字\cfrac{\sqrt{3}}{2}がsinになるような角度を探します。すると,これは\cfrac{\pi}{3}なので,\cfrac{1}{2}=\cos\cfrac{\pi}{3},\cfrac{\sqrt{3}}{2}=\sin\cfrac{\pi}{3}になるので,
2\left(\sin\theta\cdot\cfrac{1}{2}+\cos\theta\cdot\cfrac{1}{2}\right)=2\left({\color{red}\sin\theta\cos\cfrac{\pi}{3}+\cos\theta\sin\cfrac{\pi}{3}}\right)赤色の部分に注目してください。まさにこれはsinの加法定理の右辺になっているではありませんか!
ということは,加法定理の左辺の形に戻して,
2\left({\color{red}\sin\theta\cos\cfrac{\pi}{3}+\cos\theta\sin\cfrac{\pi}{3}}\right)=2{\color{red}\sin\left(\theta+\cfrac{\pi}{3}\right)}これで合成完了です。sinの加法定理の形になるように,うまく変形するというやり方を身につけましょう。
もう1つ例題を。
\sin\theta+\sqrt{3}\cos\thetaを,r\cos(\theta-\alpha)の形にしなさい。
合成はsinですることがほとんどですが、時々cosでの合成を求められることがありますので、cosでも合成できるようにしましょう。
最初の手順は同じで,sinの係数1と,cosの係数\sqrt{3}を2乗して足してルートをつけた\sqrt{1^2+(\sqrt{3})^2}=2で全体をくくります。
\sin\theta+\sqrt{3}\cos\theta=2\left(\sin\theta\cdot\cfrac{1}{2}+\cos\theta\cdot\cfrac{1}{2}\right)次に,sinについている数字\cfrac{1}{2}がsinに,cosについている数字\cfrac{\sqrt{3}}{2}がcosになるような角度を探します。sinでの合成のときとは逆ですね。
すると,これは\cfrac{\pi}{6}なので,\cfrac{1}{2}=\sin\cfrac{\pi}{6},\cfrac{\sqrt{3}}{2}=\cos\cfrac{\pi}{6}になるので,
2\left(\sin\theta\cdot\cfrac{1}{2}+\cos\theta\cdot\cfrac{1}{2}\right)=2\left(\sin\theta\sin\cfrac{\pi}{6}+\cos\theta\cos\cfrac{\pi}{6}\right)( )内の順番を変えて,
2\left({\color{red}\cos\theta\cos\cfrac{\pi}{6}+\sin\theta\sin\cfrac{\pi}{6}}\right)すると,赤色の部分がcosの加法定理の右辺の形になっているので,左辺の形に戻して,
2\left({\color{red}\cos\theta\cos\cfrac{\pi}{6}+\sin\theta\sin\cfrac{\pi}{6}}\right)=2{\color{red}\cos\left(\theta-\cfrac{\pi}{6}\right)}これで合成ができました。
cosで合成するときは,cosの加法定理の形になるように変形していきます。
暗記はほぼ不可能なので、自分でつくるしかない三角関数の公式
和から積の公式と、積から和の公式は、暗記するのが難しいので、自分で変形できるようにしましょう。
和から積の公式
sinA+sinBのように、2つの和の形になっているものを、積の形に直す公式です。
\begin{array}{l}
・\sin A+\sin B=2\sin\cfrac{A+B}{2}\cos\cfrac{A-B}{2}\\\\
・\sin A-\sin B=2\cos\cfrac{A+B}{2}\sin\cfrac{A-B}{2}\\\\
・\cos A+\cos B=2\cos\cfrac{A+B}{2}\cos\cfrac{A-B}{2}\\\\
・\cos A-\cos B=2\sin\cfrac{A+B}{2}\sin\cfrac{A-B}{2}
\end{array}気合いで覚えてもいいですが,きっと忘れてしまうので,作りかたを身につけましょう。
これらは、A=α+β、B=α-βとして、加法定理で計算することで積の形にすることができます。
AとBのうち、大きい方をα+β、小さい方をα-βとするとやりやすい。
\sin4\theta+\sin8\thetaを積の形で表しなさい。
①,②を連立させて\alphaと\betaを求めます。
4\theta=\alpha-\beta…①,8\theta=\alpha+\beta…② とおく。
①+②より,12\theta=2\alpha \therefore \alpha=6\theta
②−①より,4\theta=2\beta \therefore \beta=2\theta
4\theta=6\theta-2\theta,8\theta=6\theta+2\theta とわかったので,
\sin4\theta+\sin8\theta=\sin(6\theta-2\theta)+\sin(6\theta+2\theta)
=(\sin6\theta\cos2\theta-\cos6\theta\sin2\theta)+(\sin6\theta\cos2\theta+\cos6\theta\sin2\theta) ←加法定理
=2\sin6\theta\cos2\theta
ということで,積の形にできました。他の場合も同様です。
積から和の公式
sinAsinBのように,2つの積の形になっているものを,和の形に直す公式です。
これも一覧にしますが,覚えることはないと思います。
\begin{array}{ll}
・\sin\alpha\cos\beta=\cfrac{1}{2}\{\sin(\alpha+\beta)+\sin(\alpha-\beta)\}\\\\
・\cos\alpha\sin\beta=\cfrac{1}{2}\{\sin(\alpha+\beta)-\sin(\alpha-\beta)\}\\\\
・\cos\alpha\cos\beta=\cfrac{1}{2}\{\cos(\alpha+\beta)+\cos(\alpha-\beta)\}\\\\
・\sin\alpha\sin\beta=-\cfrac{1}{2}\{\cos(\alpha+\beta)-\cos(\alpha-\beta)\}
\end{array}これらは,加法定理の右辺を思い出して、元に戻すことを考えていきます。
例を2つほどやります。
sinαcosβの場合
\sin\alpha\cos\betaが出てくるのは,\sinの加法定理だ!
sinの加法定理(和と差)を足し引きして,\sin\alpha\cos\betaが残るようにするには,
(\sin\alpha\cos\beta+\cos\alpha\sin\beta)+(\sin\alpha\cos\beta-\cos\alpha\sin\beta)=2\sin\alpha\cos\beta
ってすればよい。つまり,
\sin(\alpha+\beta)+\sin(\alpha-\beta)=2\sin\alpha\cos\beta
両辺2で割って整理すると,
\sin\alpha\cos\beta=\cfrac{1}{2}\{\sin(\alpha+\beta)+\sin(\alpha-\beta)\}
sinαsinβの場合
\sin\alpha\sin\betaが出てくるのは,\cosの加法定理だ!
cosの加法定理(和と差)を足し引きして,\sin\alpha\sin\betaが残るようにするには,
(\cos\alpha\cos\beta+\sin\alpha\sin\beta)-(\cos\alpha\cos\beta-\sin\alpha\sin\beta)=2\sin\alpha\sin\beta
ってすればよい。つまり,
\cos(\alpha-\beta)-\cos(\alpha+\beta)=2\sin\alpha\sin\beta
両辺2で割って整理すると,
\sin\alpha\sin\beta=-\cfrac{1}{2}\{\cos(\alpha+\beta)-\cos(\alpha-\beta)\}
和から積も,積から和も,数Ⅱではあまり使う機会がないですが,加法定理から作る手順だけはおさえておきましょう。
 粗茶さん
粗茶さん数Ⅲでは,三角関数の積分で必要になります。
まとめ
今回は,三角関数の公式のうち,覚えるべきものと自分で求めるべきものをまとめました。
自分で求めるべきと紹介したものでも、何度も使っているうちに自然と覚えてしまうものですし,そうなるまで勉強してほしいところです。
数Ⅱの三角関数は一筋縄でいかないところがありますが,今回の記事が学習の助けになれれば嬉しいです。
はりきって行きましょう!
三角関数 おすすめ参考書
cosの合成までしっかり説明されているのはこの参考書!さすが坂田先生!
このブログでは,自分で勉強しているとき,つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や,勉強が楽しくなる文房具も紹介していますので,よろしければご覧ください!