2次不等式「解なし」も「すべての実数」も，すべて平方完成で解決！

学生の方

2次不等式って，因数分解のときは簡単にできるんだけど，たまに出てくる「解なし」とか「解はすべての実数」になるのが，意味わからん。

2次不等式の問題で「解なし」とか「解はすべての実数」とか「a以外のすべての実数」とか，特殊なパターンになるものが出てくると，手も足も出ない…そんなお悩みはありませんか？

実は，どんな2次不等式でも「平方完成」を使えば解けてしまいます。

特に，「解なし」とか「解はすべての実数」のような特殊なパターンのときに，平方完成が力を発揮します。

この記事では，2次関数を平方完成を用いて解く方法を，さまざまなパターンごとに説明します。

この記事を読めば，どんな形の2次方程式が出ても，もう怖くない！

学生の方

平方完成も苦手なんですが…

粗茶さん

平方完成の手順も説明するので，大丈夫ですよ！

この記事を書いた人

• 高校数学・高校公民・中学社会担当の現役塾講師
• 講師歴13年
• 13年の指導経験で知った「生徒がつまづきやすいポイント」や「教科書よりも効率の良い解法」をわかりやすく発信しています。

平方完成とは

平方完成とは，一般的に，

ax^2+bx+c

の形の式を，

a(x-p)^2+q

の形に変形することをいいます。

粗茶さん

a\neq 0です。

平方完成は，２次関数のグラフを描くときに必要になる変形なので，手順をしっかり身につけましょう。

平方完成の手順

平方完成の手順を，具体例を使って説明します。

STEP

2次の係数で最初の2項をくくる

x^2の係数があるときは，x^2の係数で最初の2項（x^2とxの項）をくくります。

\begin{array}{ll}
&2x^2-4x+5\\\\
=&2\{x^2-2x\}+5
\end{array}

粗茶さん

見やすくするために中括弧を使っていますが，普通の括弧でもいいです。

STEP

カッコ内で次の変形をする

図のように変形します。

展開してもとに戻ることを確認するといいです。

STEP

外のカッコを外して完成

最後に外のカッコ（中括弧）を外して完成です。

\begin{array}{ll}
&2\{(x-1)^2-1^2\}+5\\\\
=&2(x-1)^2-2+5\\\\
=&2(x-1)^2+3
\end{array}

x^2の係数が1のときは，手順が少なくなります。

STEP

2次の係数で最初の2項をくくる

今回はx^2の係数が1なので，あえてくくらなくてもいいですが，わかりやすいようにくくっておきます。

\begin{array}{ll}
&x^2+3x+1\\\\
=&\{x^2+3x\}+1
\end{array}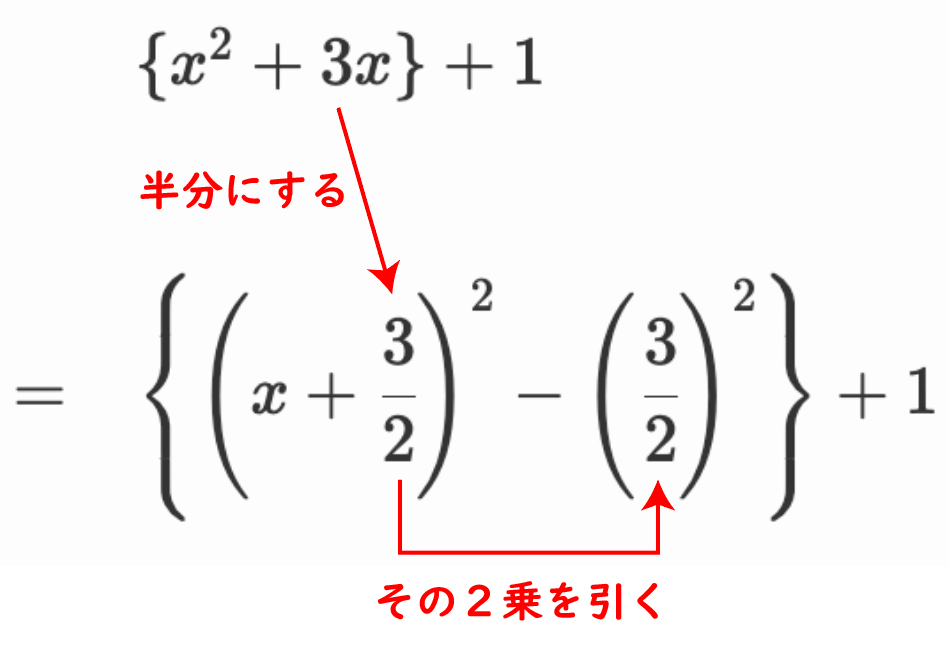

STEP

カッコ内で次の変形をする

STEP

外のカッコを外して完成

\begin{array}{ll}
&\left\{\left(x+\cfrac{3}{2}\right)^2-\left(\cfrac{3}{2}\right)^2\right\}+1\\\\
=&\left(x+\cfrac{3}{2}\right)^2-\left(\cfrac{3}{2}\right)^2+1\\\\
=&\left(x+\cfrac{3}{2}\right)^2-\cfrac{5}{4}\\\\
\end{array}

粗茶さん

xの係数が奇数のときは分数が出てくるので，計算がやや複雑になります。

x^2の係数が負のときは，符号を間違えやすいですが，手順を守れば大丈夫！

STEP

2次の係数で最初の2項をくくる

\begin{array}{ll}
&-3x^2+2x+4\\\\
=&-3\left\{x^2-\cfrac{2}{3}x\right\}+4
\end{array}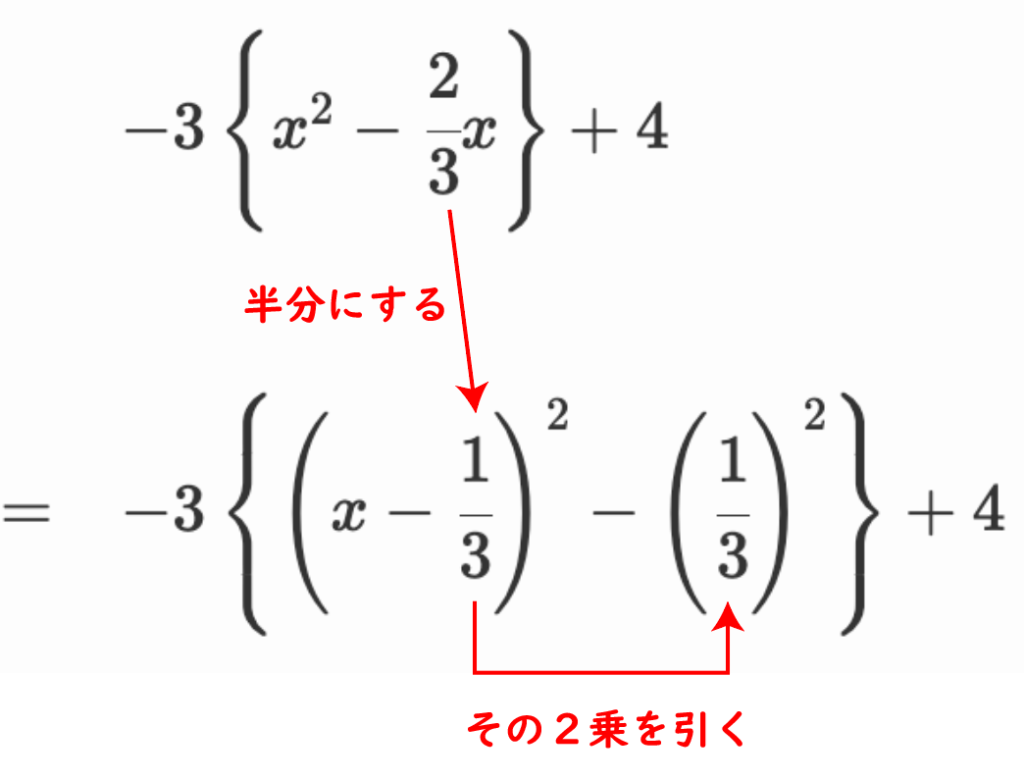

STEP

カッコ内で次の変形をする

STEP

外のカッコを外して完成

\begin{array}{ll}
&-3\left\{\left(x-\cfrac{1}{3}\right)^2-\left(\cfrac{1}{3}\right)^2\right\}+4\\\\
=&-3\left(x-\cfrac{1}{3}\right)^2+3\cdot\left(\cfrac{1}{3}\right)^2+4\\\\
=&-3\left(x-\cfrac{1}{3}\right)^2+\cfrac{13}{3}
\end{array}

粗茶さん

今は説明用に細かく途中式を書いていますが，慣れたら省略してもOK。

2次不等式を平方完成を使って解く

それでは，2次不等式を平方完成で解いてみます。

準備として，以下の基本的な形をおさえておきましょう。

\left\{
\begin{array}{l}
x^2>a　\Leftrightarrow　x <-\sqrt{a}，\sqrt{a} < x\\\\
x^2< a　\Leftrightarrow　-\sqrt{a}< x < \sqrt{a}
\end{array}
\right.

粗茶さん

2次方程式のノリで
x<\pm a
みたいな書き方はしない（というより意味がわからない）ので，注意しましょう。

因数分解できるときは，因数分解でしょうね。

x^2-x-6<0

左辺が因数分解できるので，一般的には因数分解を使います。

\begin{array}{rcl}
x^2-x-6 &<&0\\\\
(x+2)(x-3)&<&0
\end{array}

\therefore　-2< x<3　\cdots(答)

あえて平方完成を用いて解くと，次のようになります。

\begin{array}{rcl}
x^2-x-6 &<&0\\\\
\left(x-\cfrac{1}{2}\right)^2-\cfrac{1}{4}-6&<&0\\\\
\left(x-\cfrac{1}{2}\right)^2&<&\cfrac{25}{4}\\\\
\end{array}

\begin{array}{c}
-\cfrac{5}{2}< x-\cfrac{1}{2}<\cfrac{5}{2}\\\\\\
\therefore　-2< x<3
\end{array}

学生の方

いやいやいや，こんな風に解く人いないでしょ。

粗茶さん

因数分解できるときは平方完成する必要はありません。
そちらのほうが圧倒的に楽ですからね。
平方完成でもできるということをわかってもらえればOK。

解の公式が必要なケースは，平方完成のほうが解答が書きやすいかも

x^2+5x+2\geqq 0

これは左辺が因数分解できません。

解の公式で「=0」の解を求めるやり方が一般的でしょうか。

x^2+5x+2=0

x=\cfrac{-5\pm\sqrt{5^2-4\cdot 1\cdot 2}}{2\cdot 1}=\cfrac{-5\pm\sqrt{17}}{2}

x\leqq \cfrac{-5-\sqrt{17}}{2}，\cfrac{-5+\sqrt{17}}{2} \leqq x

これは，平方完成でやったほうが書きやすいかも。

\begin{array}{rcl}
x^2+5x+2\geqq 0\\\\
\left(x+\cfrac{5}{2}\right)^2-\cfrac{25}{4}+2\geqq 0\\\\
\left(x+\cfrac{5}{2}\right)^2\geqq\cfrac{13}{4}\\\\
x+\cfrac{5}{2}\leqq-\cfrac{\sqrt{13}}{2}，\cfrac{\sqrt{13}}{2}\leqq x+\cfrac{5}{2}\\\\
\therefore x\leqq\cfrac{-5-\sqrt{13}}{2}，\cfrac{-5+\sqrt{13}}{2}\leqq x
\end{array}

学生の方

途中で日本語が入らなくてもいけるところは認めますが，短くなってはいない…

今の例のように，答えが分数になるときは，あまり恩恵を感じられませんが，

二次関数の問題で，最初に平方完成で頂点を求める問題があって，そのあとに不等式を解かせるようなパターンの場合は，有効だと思います。

粗茶さん

状況に応じて使い分けることが大事！

「解なし」「すべての実数」などになるパターンも暗記せずに解く

「左辺＝0」の解が異なる2つの実数にならない場合は，不等式の解が「解なし」とか「すべての実数」とか，特殊な形になります。

学生の方

「解なし」とか「すべての実数」とか，表になっているのを習ったんだけど，多すぎて覚えられないっす。

表というのは，これです。

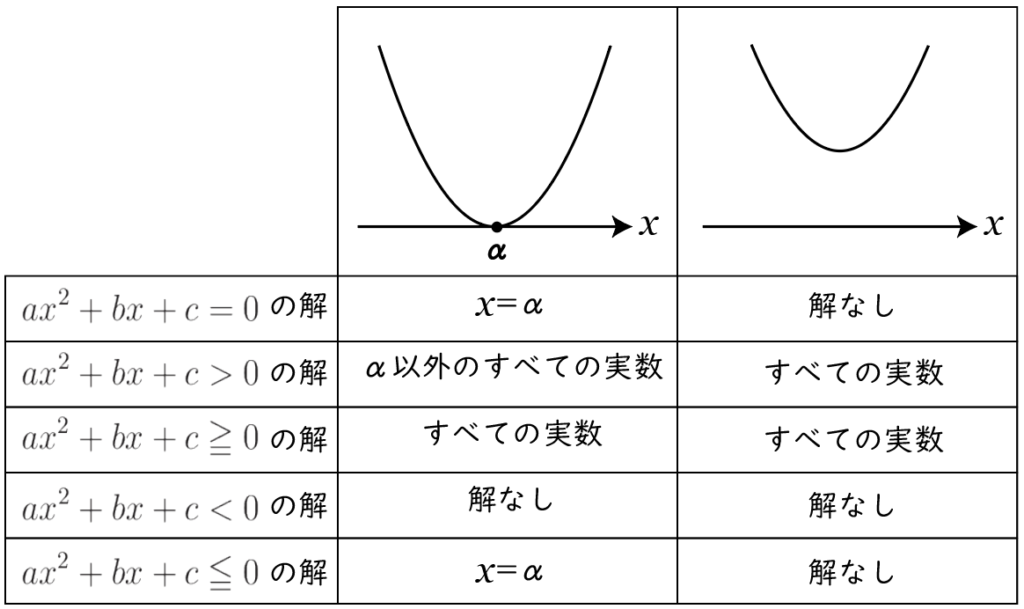
不等式だけでも8パターンもあるので，覚えるのはほぼ不可能といえます。

このような状況でも，平方完成して解く方法ならば，暗記せずに解くことができます。

ここで次の事実を確認しておきたい!!

\Large{a^2\geqq 0}

「実数の２乗は必ず0以上」ですね。

言い換えれば，「2乗して負になる実数は存在しない」ということになります。

「2乗は0以上」の性質を使って，特殊パターンの不等式を解いていきます。

x^2-10x+25<0

(x-5)^2<0\cdots①

9x^2-6x+1\leqq 0

(3x-1)^2\leqq 0\cdots②

\begin{array}{l}(3x-1)^2=0\\\\
3x-1=0\\\\
\therefore　x=\cfrac{1}{3}\cdots(答)
\end{array}

x^2-6x+11>0

\begin{array}{l}
(x-3)^2-9+11>0\\\\
(x-3)^2>-2\cdots③
\end{array}

x^2-2x+1>0

(x-1)^2>0\cdots④

実質，2次関数のグラフを考えているのと同じではあるのですが，

「2乗は0以上」という1点に絞って考えることで，暗記することを極力減らして，自力で答えを出せるようになります。

また，特殊パターンは突然出てくるので，普段から平方完成で考えるようにしておくと，迷わずに解答が書けると思います。

2次不等式に平方完成という選択肢を！

この記事では，2次不等式を平方完成を用いて解く方法を説明しました。

平方完成は，「解なし」「すべての実数」などになる場合の2次不等式では特に有効です。

すべての場合で平方完成が早いということはありませんが，解答方法の選択肢としてすぐに使えるようにしておきましょう。

　

このブログでは，自分で勉強しているとき，つまづきやすいポイントを解説。

「かゆいところに手が届く」情報を発信しています。

自分で勉強する際にオススメの参考書や，勉強が楽しくなる文房具も紹介していますので，よろしければご覧ください！

あわせて読みたい

製図用シャープで楽しく勉強！ノートがパッと華やぐ！ ノートが汚くて自分でも読めないときがあるんだよね。 「製図用シャープ」があなたのノートのお悩みを解決します。 製図用シャープは、ただの筆記具ではありません。 あ…

あわせて読みたい

塾講師直伝！高校数学の学習法〜問題集を効率よく進めて知識を自分のものに！ 入試で数学が必要なあなた、模試や過去問を解こうとしても、全然手がつけられなくて悩んでいませんか？ 問題が解けないのは、数学のセンスがないからかなあ… 実は、数学…

あわせて読みたい

【高校生】数学が全くわからないあなたへ！自分で勉強できるおすすめ参考書ガイド 数学の先生が変わって， 先生が何言ってるか全然わからない。ピンチ… という状況で悩んでいませんか？ 私も高校生の時，そうでした。 高１のときの先生はよかったけど，…