 学生の方
学生の方シグマの計算で,意味不明な変形が出てきたんだけど…
\displaystyle{\sum^{n}_{k=1}\cfrac{1}{k(k+2)}=\sum^{n}_{k=1}\cfrac{1}{2}\left(\cfrac{1}{k}-\cfrac{1}{k+2}\right)} 学生の方
学生の方どうして引き算になったの??2分の1は何??
このように,分母が多項式の積になっている分数を,足し算や引き算の形に分けることを部分分数分解といいます。
ぶぶんぶんすうぶんかい …って冗談みたいな名前ですが,本気です。
数列の問題の中では頻出パターンの部分分数分解ですが,学校の授業でさらっと扱われてしまって,意味がよくわかっていない人もいるのではないでしょうか?
この記事では,数列の和の問題で使う部分分数分解のやりかたをわかりやすく解説します。
2つの積だけでなく,3つの積の場合も扱います。
この記事を読めば,部分分数分解はこわくない !
- 部分分数分解のやりかたがわかる
- 部分分数分解を用いた数列の和の求めかたがわかる
- 3つの積の形になっている式の部分分数分解のやりかたがわかる

粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

部分分数分解は通分の逆
部分分数分解とは,分母が多項式の積の形になっている分数を,複数の分数に分けることです。
\cfrac{5x-5}{(x-3)(x+2)}=\cfrac{2}{x-3}+\cfrac{3}{x+2}分母が(x-3)(x+2)の形の分数を、分母がx-3の分数と分母がx+2の分数に分けています。
異なる分母の分数に分けているので、部分分数分解は通分の逆ということになります。
 学生の方
学生の方意味はわかったけど、どうやって計算するの?
 粗茶さん
粗茶さん手順があるので、やりかたを覚えてしまいましょう。
部分分数分解で差の形をつくる
部分分数分解を用いて数列の和を求める問題を、具体的に解いていきましょう。
まずは1問目。
次の数列の和を求めよ。
\displaystyle \sum^{n}_{k=1}\cfrac{1}{k(k+2)}分母がkとk+2の積の形になっているので、部分分数分解ができます。
 学生の方
学生の方\cfrac{1}{k}+\cfrac{1}{k+2}みたいにするの?
 粗茶さん
粗茶さん数列の和の問題のときは、\cfrac{1}{k}-\cfrac{1}{k+2}のように、差の形にします。(理由は後ほどわかります)
部分分数分解の手順は、次のようになります。
- とりあえず差の形をつくる
- 通分する
- 元の形に一致しているか確認
順にやっていきましょう。
\cfrac{1}{k}-\cfrac{1}{k+2}\cfrac{1}{k}-\cfrac{1}{k+2}=\cfrac{k+2-k}{k(k+2)}= \cfrac{2}{k(k+2)}通分した結果、
\cfrac{1}{k}-\cfrac{1}{k+2}=\cfrac{2}{k(k+2)}ということがわかりました。順番を入れ替えると、
\cfrac{2}{k(k+2)}=\cfrac{1}{k}-\cfrac{1}{k+2}これより、
\cfrac{1}{k}-\cfrac{1}{k+2} は \cfrac{\color{red}2}{k(k+2)} と同じだということがわかりました。
ですが、今は \cfrac{\color{red}1}{k(k+2)} を計算したいので、両辺を2で割って、
\cfrac{1}{k(k+2)}=\cfrac{1}{2}\left(\cfrac{1}{k}-\cfrac{1}{k+2}\right)これで完成。
この結果を使って、問題を解いてきます。
\begin{array}{lll}
&&\displaystyle{\sum^{n}_{k=1}\cfrac{1}{k(k+2)}}\\\\&=& \displaystyle{\sum^{n}_{k=1}\cfrac{1}{2}\left(\cfrac{1}{k}-\cfrac{1}{k+2}\right)}\\\\
&=&\displaystyle{\cfrac{1}{2}\sum^{n}_{k=1}\left(\cfrac{1}{k}-\cfrac{1}{k+2}\right)}\\\\
&=&\cfrac{1}{2}\left\{\left(\cfrac{1}{1}-\cfrac{1}{3}\right)+ \left(\cfrac{1}{3}-\cfrac{1}{5}\right)+\cdots + \left(\cfrac{1}{n}-\cfrac{1}{n+2}\right)\right\}\cdots(★)\\\\
&=&\cfrac{1}{2}\left(1-\cfrac{1}{n+2}\right)\\\\
&=&\cfrac{1}{2}\cdot\cfrac{n+2-1}{n+2}\\\\
&=&\cfrac{n+1}{2n+4} \cdots(答)
\end{array}kに1からnまでを順に代入して足すと、(★)のようになりますが、両端の \cfrac{1}{1}と-\cfrac{1}{n+2}以外は、隣同士がプラスとマイナスで打ち消しあって、なくなります。
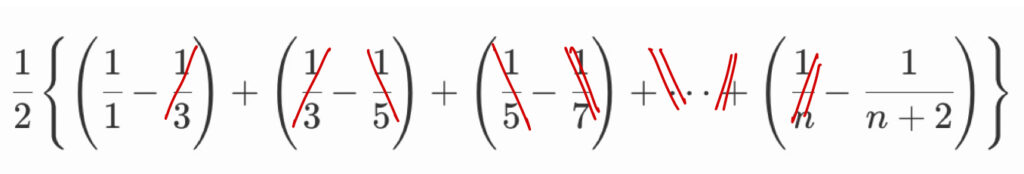
ということで、分母が積の形になっている数列の和は、
- とりあえず差の形を作る
- 通分する
- 元の形に合うように調整
という手順で部分分数分解をしましょう。
3つの積の部分分数分解も、2つに分ける
次は、3つの積になっているバージョンをやってみましょう。
次の数列の和を求めよ。
\displaystyle \sum^{n}_{k=1}\cfrac{1}{(2k-1)(2k+1)(2k+3)} 学生の方
学生の方3つの積だから、3つに分ける?
 粗茶さん
粗茶さん3つに分ける方法もあるんですが、数列の和の場合は2つに分けます。
3つの積の形を部分分数分解するときは、真ん中を重複させて、2つに分けます。
真ん中の2k+1を両方につける形で、2つの差にします。
\cfrac{1}{(2k-1)(2k+1)}-\cfrac{1}{(2k+1)(2k+3)}\begin{array}{ll}
&\cfrac{1}{(2k-1)(2k+1)}-\cfrac{1}{(2k+1)(2k+3)}\\\\
=&\cfrac{(2k+3)-(2k-1)}{(2k-1)(2k+1)(2k+3)}\\\\
=&\cfrac{4}{(2k-1)(2k+1)(2k+3)}
\end{array}通分した結果、
\cfrac{1}{(2k-1)(2k+1)}-\cfrac{1}{(2k+1)(2k+3)}
=\cfrac{4}{(2k-1)(2k+1)(2k+3)}ということがわかりました。
順番を入れ替えて、
\cfrac{4}{(2k-1)(2k+1)(2k+3)}=\cfrac{1}{(2k-1)(2k+1)}-\cfrac{1}{(2k+1)(2k+3)}両辺を4で割って、
\cfrac{1}{(2k-1)(2k+1)(2k+3)}=\cfrac{1}{4}\left\{\cfrac{1}{(2k-1)(2k+1)}-\cfrac{1}{(2k+1)(2k+3)}\right\}これで完成。
これをつかって問題を解いていきます。
\begin{array}{lll}
&&\displaystyle\sum^{n}_{k=1}\cfrac{1}{(2k-1)(2k+1)(2k+3)}\\\\
&=& \displaystyle\sum^{n}_{k=1}\cfrac{1}{4}\left\{\cfrac{1}{(2k-1)(2k+1)}-\cfrac{1}{(2k+1)(2k+3)}\right\}\\\\
&=& \cfrac{1}{4} \displaystyle\sum^{n}_{k=1}\left\{\cfrac{1}{(2k-1)(2k+1)}-\cfrac{1}{(2k+1)(2k+3)}\right\}\\\\
&=&\cfrac{1}{4}\left\{\cfrac{1}{1\cdot 3}-\cfrac{1}{3\cdot 5}+ \cfrac{1}{3\cdot 5}-\cfrac{1}{5\cdot 7}+\cdots+\cfrac{1}{(2n-1)(2n+1)}-\cfrac{1}{(2n+1)(2n+3)}\right\}\\\\
&=&\cfrac{1}{4} \left\{\cfrac{1}{1\cdot 3}-\cfrac{1}{(2n+1)(2n+3)}\right\}\\\\
&=&\cfrac{1}{4}\cdot \cfrac{(2n+1)(2n+3)-3}{3(2n+1)(2n+3)}\\\\
&=&\cfrac{4n^2+5}{12(2n+1)(2n+3)} \cdots(答)
\end{array}やはり、kに1から順に代入すると、両端以外はプラスとマイナスで打ち消されて、なくなります。
3つの積の形は、真ん中を重複させて、2つの差に直すことがポイントです。
まとめ
この記事では、数列の和を求める時に登場する部分分数分解のやり方を説明しました。
数学の問題では、最終的に変形された形を覚えておいて、そこから逆にたどり、最初の形と比較するという流れがよくあります。
部分分数分解のその一つです。
数学はひらめきがないと解けないイメージがあるかもしれませんが,実際は知識と経験がかなりのウェイトを占めます。
自分の脳内に知識を蓄えて,適切なときに引き出せるようにしていきたいですね!
このブログでは,自分で勉強しているとき,つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や,勉強が楽しくなる文房具も紹介していますので,よろしければご覧ください!



