学生の方群数列が全然わかりません！
数列の中でも苦手な人の多さで上位に位置するのが群数列。
なんだかごちゃごちゃしてて意味がわからない！って悩んでいませんか？
実は，群数列は「項数に注目する」「表にまとめる」ことでスッキリと解くことができてしまいます。
この記事では，群数列の問題の解き方をわかりやすく説明していきます。
群数列は解き方をマスターしてしまえば，大きな得点源になります。
群数列を得意分野にして，周りに差をつけちゃいましょう！
- 群数列の問題の解き方がスッキリ理解できる
- 高校数学・高校公民・中学社会担当の現役塾講師
- 講師歴13年
- 13年の指導経験で知った「生徒がつまづきやすいポイント」や「教科書よりも効率の良い解法」をわかりやすく発信しています。
「〜までの項数」＝「〜が何番目か」
群数列の問題に入る前に，一つ確認しておきたいことがあります。それは，
「〜までにいくつの項があるか」と「〜は何番目か」は同じ意味だということ。
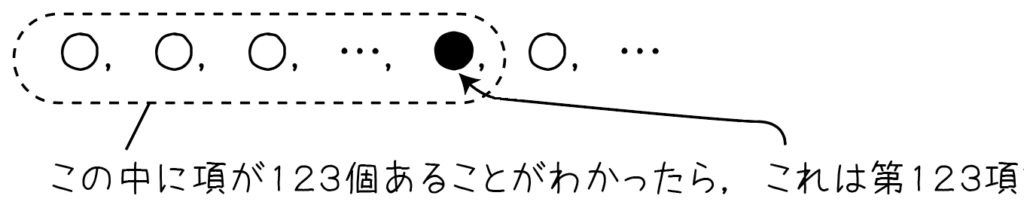
群数列は，項数に注目することが最重要ポイントなので，しっかり確認しておきましょう。
群数列は項数を追え！
まずは，項数に注目しやすい問題をやってみましょう。
1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,\cdots
のように，自然数nがn個ずつ並んでいる数列がある。
(1)初めて30が現れるのは，第何項か。
(2)第200項を求めよ。
(3)初項から第200項までの和を求めよ。
1が1個，2が2個，3が3個…と続いているので，次のように群に分けます。
横長になってしまうので，表にまとめるとわかりやすくなります。
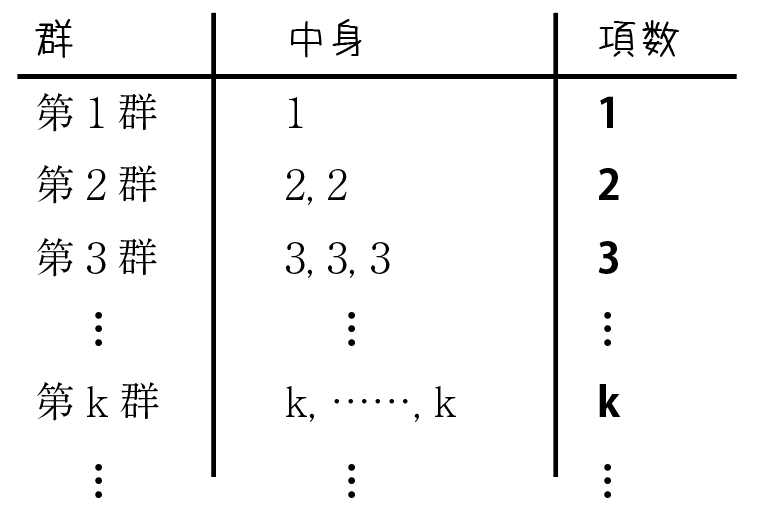
そして，一番右の列の項数に注目することが大切です。
(1)初めて現れる30は，第何項か。
(1)は，「初めて現れる30は，最初から数えると第何項ですか？」というご質問です。
第30群付近を表に書いて考えてみましょう。
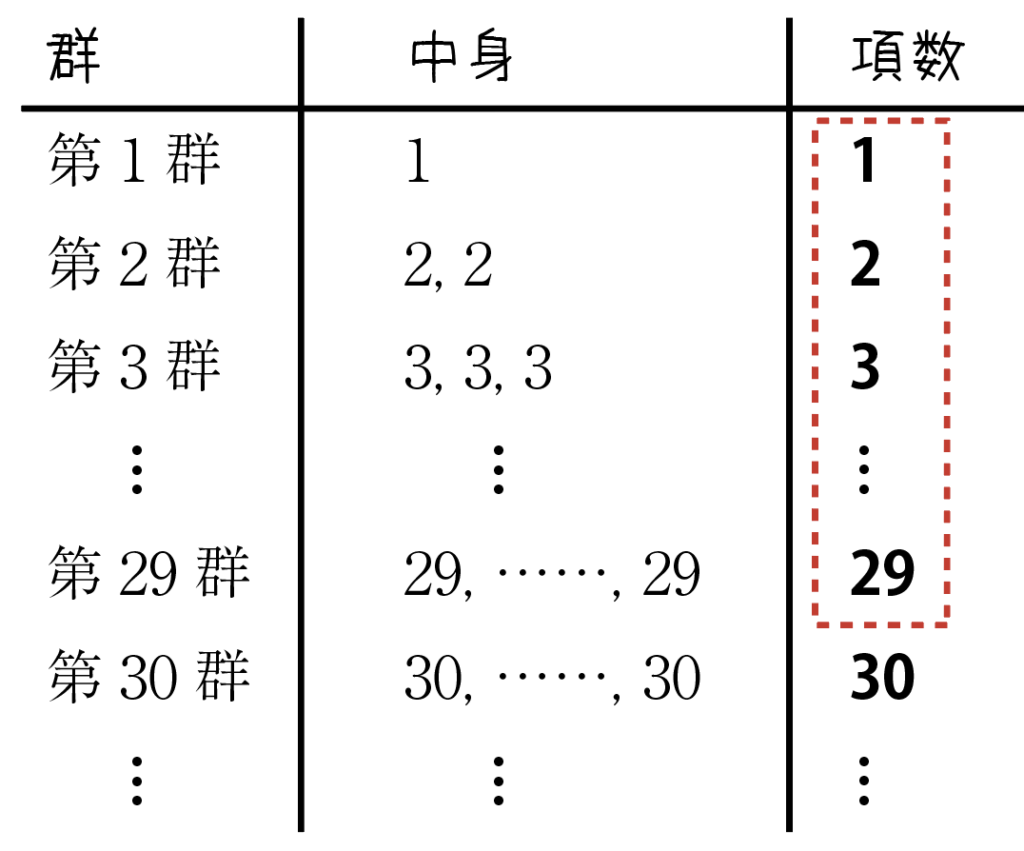
「初めて現れる30」は，第30群の最初の項ですね。
一つ手前の第29群までには，
1+2+3+\cdots+29個の項が入っています。（上表の赤枠）
第30群の最初の項は，そのすぐ次なので，1足して，
1+2+3+\cdots+29+1番目の項，ということになります。
よって，初めて30が現れるのは，
\begin{aligned}& 1+2+3+\cdots+29+1\\\\&=\sum^{29}_{k=1}k+1\\\\&=\cfrac{1}{2}\cdot29\cdot30+1\\\\&=436\end{aligned}より，第436項 …（答）
(2)第200項を求めよ。
まず，第200項が第何群に含まれるか？を考えます。
第200項が第n群に含まれるとすると，
第200項は，第n-1群の最後の項と，第n群の最後の項の間にあります。
表にすると，次のようになります。
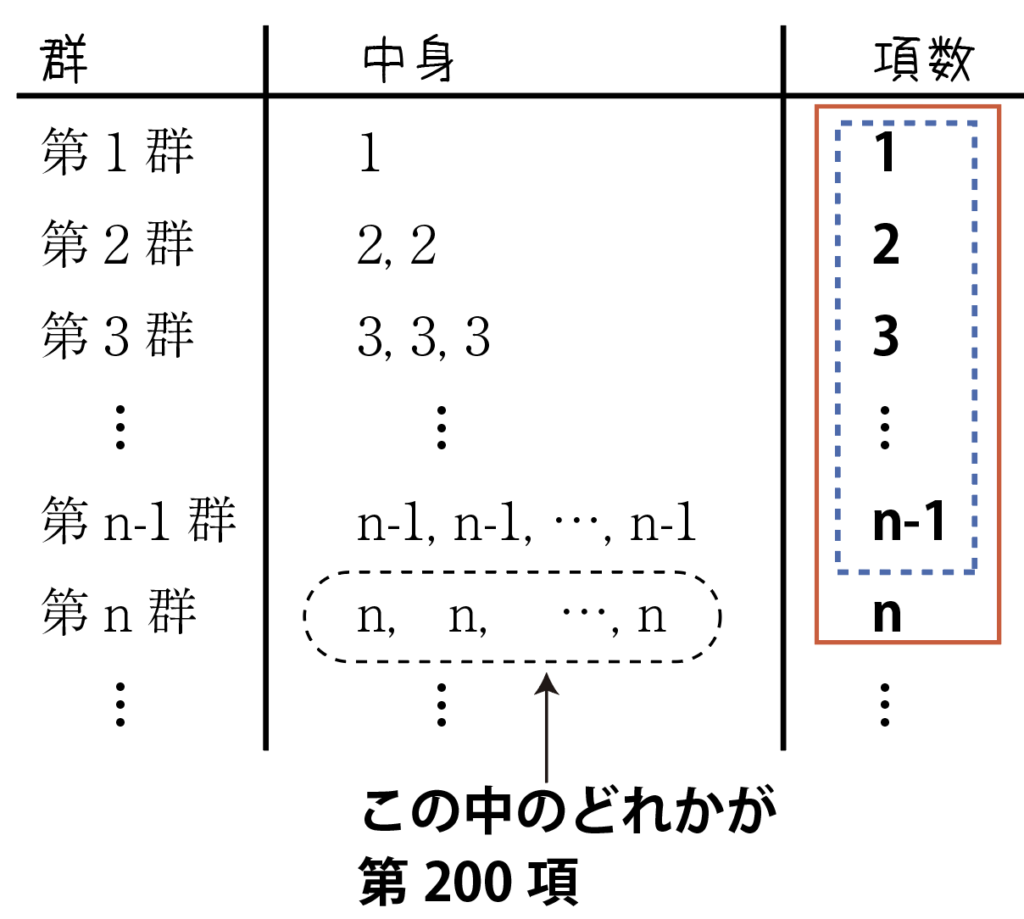
第n-1群までの項数（上表の青枠）は，
1+2+\cdots+(n-1)=\displaystyle{\sum^{n-1}_{k=1}k}=\cfrac{1}{2}(n-1)n（個）第n群までの項数（上表の赤枠）は，
1+2+\cdots+n=\displaystyle{\sum^{n}_{k=1}k}=\cfrac{1}{2}n(n+1)（個）で，200がこれらの間にあるので，
\cfrac{1}{2}(n-1)n<200\leqq\cfrac{1}{2}n(n+1)
粗茶さん第200項が，ちょうど第n群の最後の項という可能性もあるので，右側の不等号にはイコールをつけておきます。
この不等式の各辺を２倍して，
(n-1)n<400\leqq n(n+1)
ここで，二次不等式を解けばいいわけなのですが，まともに計算しようとしても解けません。
そこで，nが自然数であることに注目して，てきとうな数字を代入して，成り立つかどうかを調べていきます。
今回は，20×20が400なので，20あたりに答えがありそうです。
n=18のとき，(n-1)n=17\cdot18=306，n(n+1)=18\cdot19=342 で，×\\n=19のとき，(n-1)n=18\cdot19=342，n(n+1)=19\cdot20=380 で，×\\n=20のとき，(n-1)n=19\cdot20=380，n(n+1)=20\cdot21=420 で，◯
ということで，不等式をみたすnは20ということがわかりました。
よって，第200項は第20群にあることが判明。
第20群に含まれる項はすべて20なので，第200項は20ということになります。…（答）
(3)初項から第200項までの和を求めよ。
(2)で，第200項は第20群にあることはわかりました。
第200項までの和を求めるには，第200項が第20群の何番目かを求める必要があります。
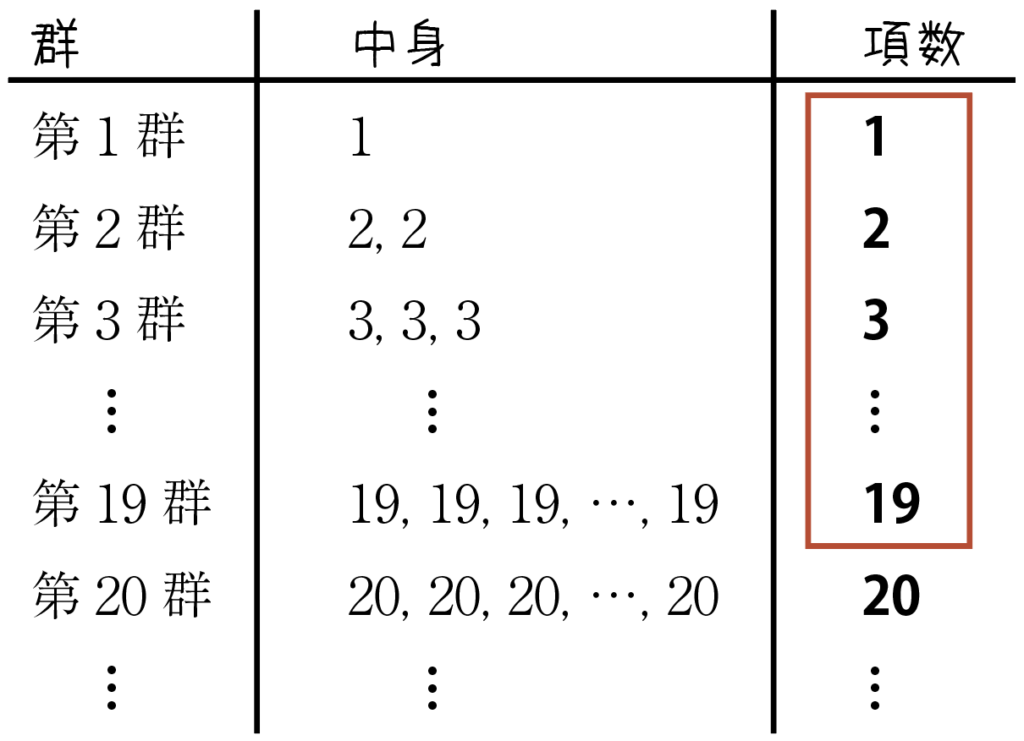
第19群までの項数（上表の赤枠）は，
\begin{aligned}& 1+2+3+\cdots+19\\\\&=\sum^{19}_{n=1}k\\\\&=\cfrac{1}{2}\cdot19\cdot20\\\\&=190（個）\end{aligned}なので，第200項は，第20群の200-190=10番目なのだ。
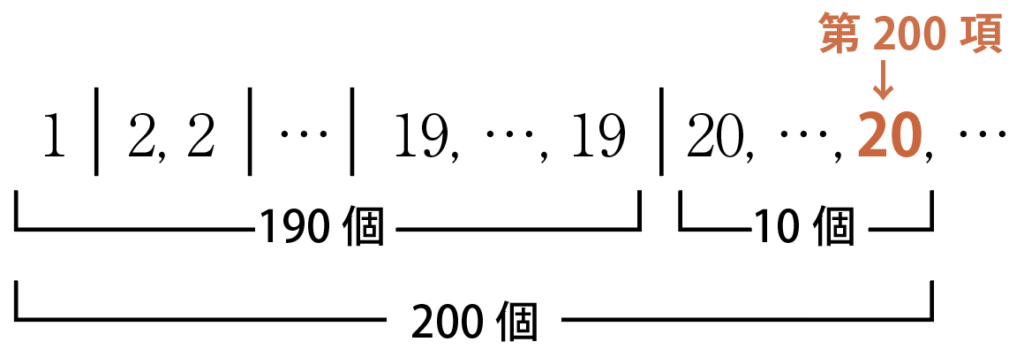
ということで，第200項までの和は，
1が1個，2が2個，3が3個，…，19が19個と，20が10個なので，
\begin{aligned}& 1\times1+2\times2+3\times3+\cdots+19\times 19+20\times10\\\\&=1^2+2^2+3^3+\cdots 19^2+20\times10\\\\&=\sum^{19}_{k=1}k^2+20\times 10\\\\&=\cfrac{1}{6}\cdot19\cdot 20\cdot 39+200\\\\&=2670 …（答）\end{aligned}普通の数列を群に分けた場合でも，項数に注目！
群数列には，普通の数列（等差数列や等比数列）を群に分けて作られたものもあります。
基本的なやり方は同じで，あくまで項数に注目していくことが大切です。
初項2，公差3の等差数列を，
2,5｜8,11,14,17｜20,23,26,29,32,35｜38,41\cdots
のように，２個，4個，6個，8個…と区切って群に分け，左から第1群，第2群，…とよぶとき，
(1)第10群の4番目の数を求めよ。
(2)335は第何群の何番目の数か。
(3)第n群の初項を求めよ。
(4)第n群に含まれる数の総和を求めよ。
普通の数列を区切った問題の場合は，最初に群の切れ目をなくした数列の一般項を求めておきます。
2,5,8,11,14,17,20,23,26,29,32,35,38,41\cdots
初項2，公差3の等差数列になっているので，一般項a_Nは，
\begin{aligned}a_N&=2+(N-1)\cdot3\\\\&=3N-1\end{aligned}粗茶さん小文字のnは群の番号に使うので，あえて大文字のNを使わせていただいております。
一般項を求めたあとは，項数に注目して考えていきます。
表にまとめてみます。
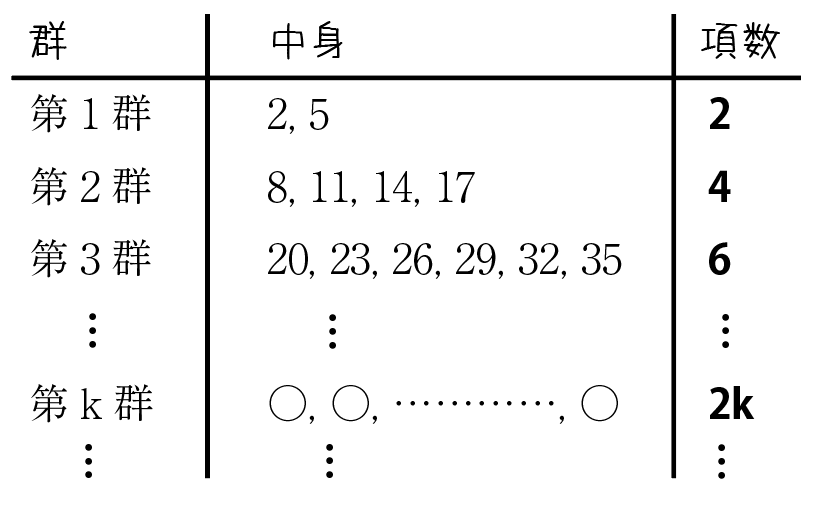
今回は，第1群には1×2=2項，第2群に2×2=4項，第3群に3×2=6項…なので，第k群にはk×2=2k項あることがわかります。
(1)第10群の4番目の数を求めよ。
第10群の4番目が，全体の何番目かが分かれば，それを一般項のNに代入して終了です。
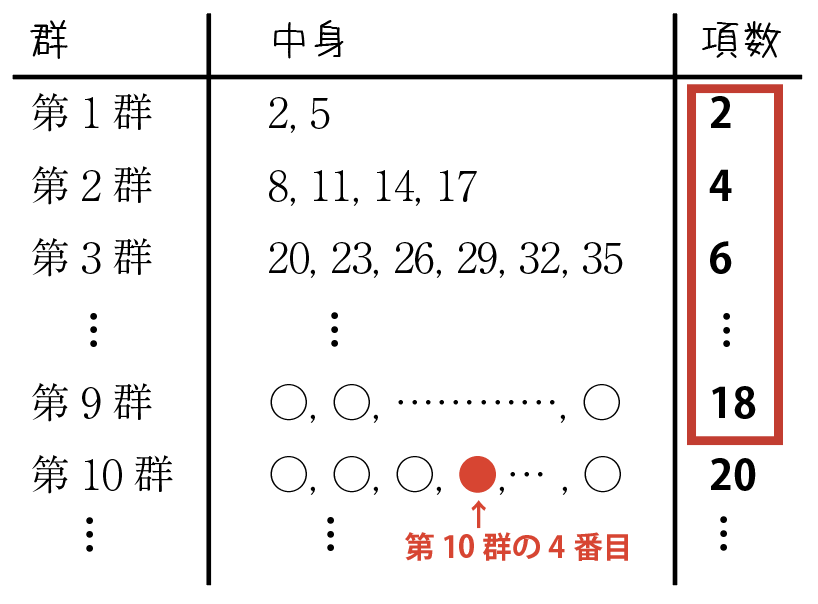
第9群までの項数は，上表の赤枠の合計で，2+4+\cdots +18（個）
第10群の4番目は，そこからさらに4つ先なので，そこまでの項数は，
\begin{aligned}
2+4+6+\cdots+18+4&=\sum^9_{k=1}2k+4\\\\
&=2\cdot\cfrac{1}{2}\cdot9\cdot10+4\\\\
&=94（個）
\end{aligned}なので，一般項3N-1のNに94を代入して，求める項は，
\begin{aligned}
3\cdot94-1=281
\end{aligned}(2)335は第何群の何番目の数か。
335というのは，項の値であって，項数ではないことに注意しましょう。
粗茶さんここで言っている335は「335番目の項」という意味ではないですよね。
まずは335が元の数列の何番目の項かを求めます。
\begin{aligned}
& a_N=335\\\\
&\Leftrightarrow 3N-1=335\\\\
&\therefore N=112
\end{aligned}つまり，335は，元の数列の112番目の項ということがわかりました。
ここからは，例題１と同じ流れです。
次に，112番目の項が第何群に含まれるかを考えましょう。
112番目の項が第n群にあるとすると，
表にすると次のように。
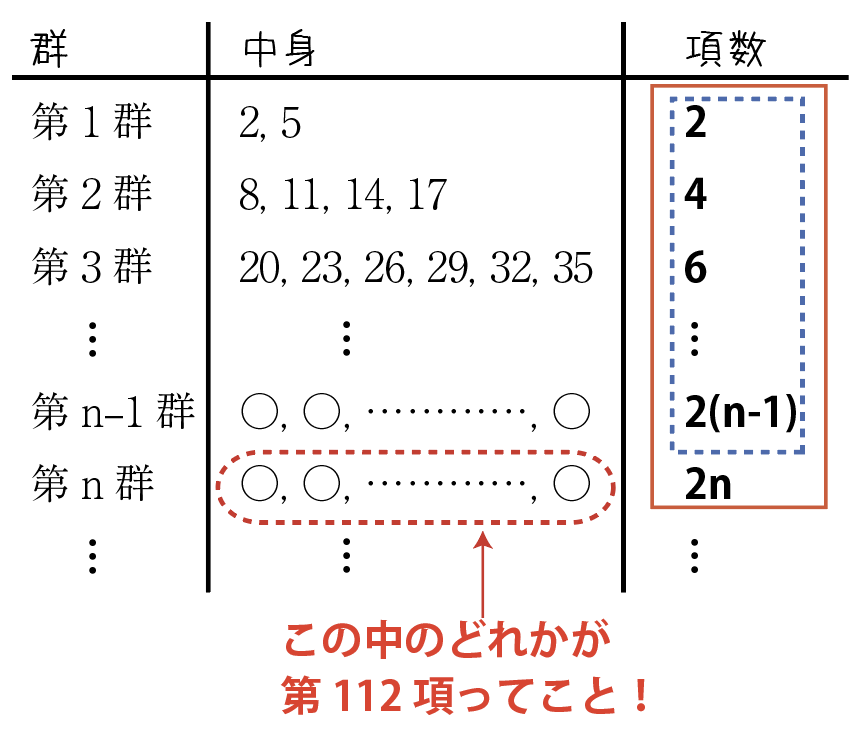
第112項は，第n-1群の最後の項と，第n群の最初の項の間にあります。
第n-1群までの項数（上表の青枠）は，
2+4+\cdots+2(n-1)=\displaystyle{\sum^{n-1}_{k=1}2k}=2\cdot\cfrac{1}{2}(n-1)n=(n-1)n（個）第n群までの項数（上表の赤枠）は，
2+4+\cdots+2n=\displaystyle{\sum^{n}_{k=1}k}=2\cdot\cfrac{1}{2}n(n+1)=n(n+1)（個）これらの間に112があるので，
(n-1)n<112\leqq n(n+1)
粗茶さん第112項が，ちょうど第n群の最後の項という可能性もあるので，右側の不等号にはイコールをつけておきます。
やはり今回も，nにてきとうな数字を代入して，成り立つかどうかを調べていきます。
今回は，10×10が100なので，10あたりを調べます。
n=10のとき，(n-1)n=9\cdot10=90，n(n+1)=10\cdot11=110 で，×\\n=11のとき，(n-1)n=10\cdot11=110，n(n+1)=11\cdot12=132 で，◯
ということで，不等式をみたすnは11ということがわかりました。
つまり，112番目の項（すなわち335）は第11群にあることがわかりました。
あとは，第11群の何番目にあるかを見つければ終了です。
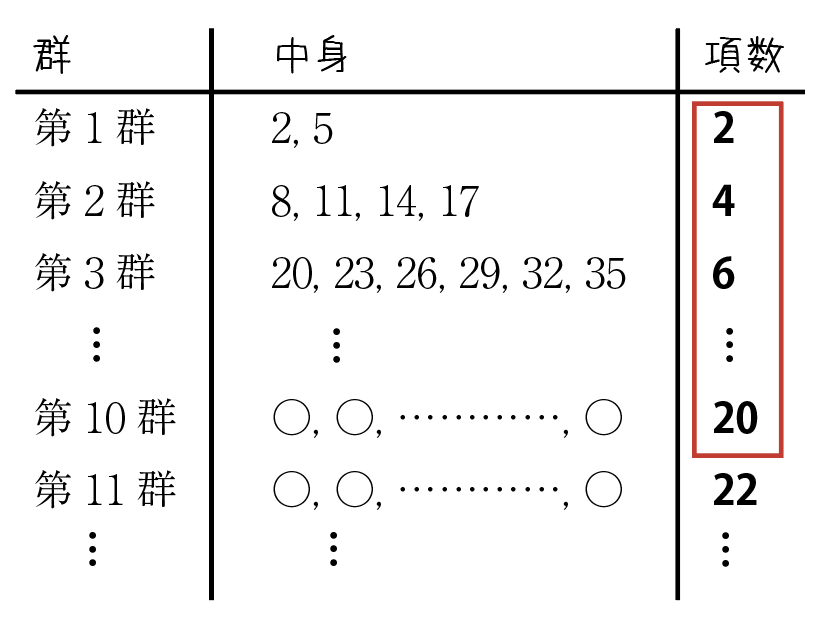
第10群の最後までの項数（表の赤枠）は，
2+4+\cdots +20=\sum^{10}_{k=1}2k=2\cdot\cfrac{1}{2}\cdot10\cdot11=110（個）ここで，112-110＝2より，
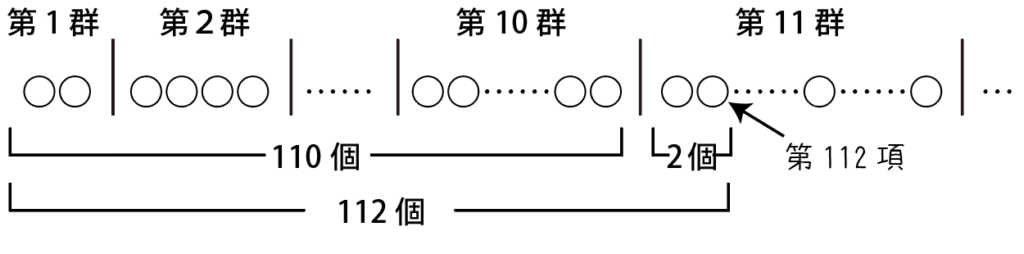
112番目の項（つまり335）は，第11群の2番目 …（答）
(3)第n群の初項を求めよ。
(3)は意外と単純です。
「第n群の初項」が元の数列の何番目の項か？を求めて，一般項のNに代入すればOKです。
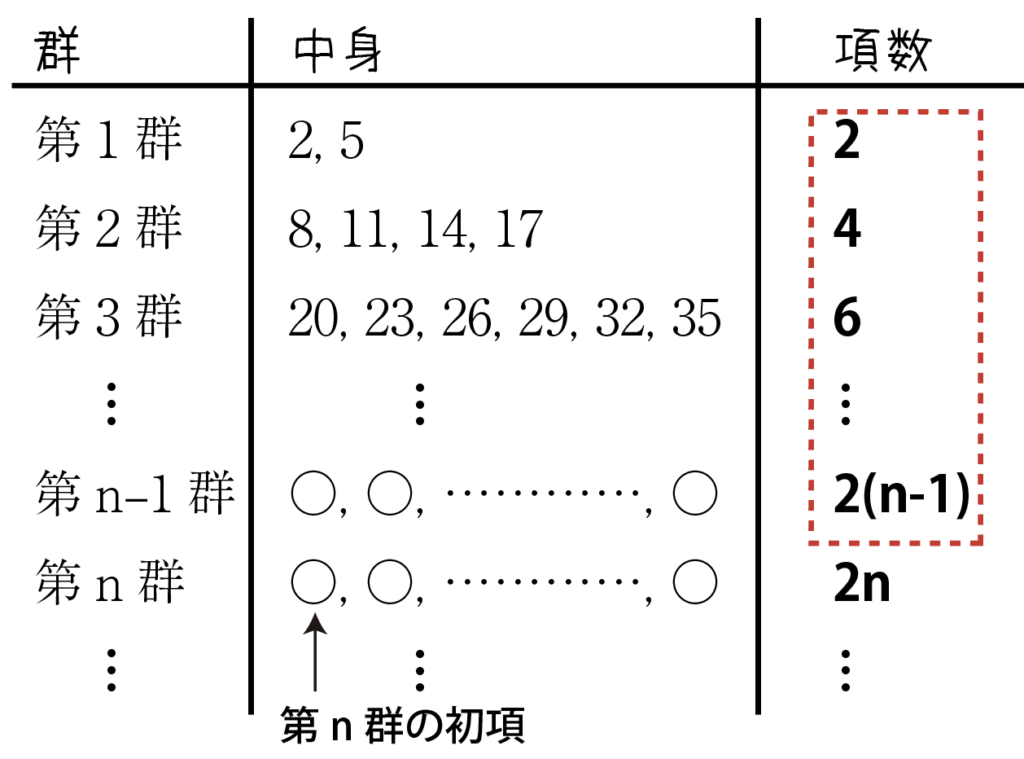
第n-1群までの項数（上表の赤枠）は，
2+4+6+\cdots+2(n-1)=\sum^{n-1}_{k=1}2k=2\cdot\cfrac{1}{2}(n-1)n=n^2-n（個）で，その次の項が「第n群の初項」なので，それはn^2-n+1（番目）ということ。
これを一般項3N-1のNに代入して，第n群の初項は，
3(n^2-n+1)-1=3n^2-3n+2
これが答えです。
(4)第n群に含まれる数の総和を求めよ。
元の数列が公差3の等差数列なので，第n群だけを抜き出しても，やはり公差3の等差数列です。
第n群は，初項3n^2-3n+2，公差3，項数2nの等差数列になっているので，公式通りに和を求めるだけです。
初項a，公差d，項数nの等差数列の和は，
\cfrac{n}{2}\{2a+(n-1)d\}今回は初項\color{red}aの代わりに\color{red}3n^2-3n+2，公差\color{blue}dの代わりに\color{blue}3，項数\color{green}nの代わりに\color{green}2nが入るので，求める和は，
\begin{aligned}
& \cfrac{\color{green}2n}{2}\{2({\color{red}3n^2-3n+2})+({\color{green}2n}-1)\cdot{\color{blue}3}\}\\\\
&=n(6n^2+1)\\\\
&=6n^3+n
\end{aligned}まとめ：群数列はとにかく項数を追いかけよう
今回は，群数列の基本的な解き方を紹介しました。
すべての問題形式を網羅することは難しいですが，いずれにせよ，項数を追いかけることが最大のポイントです。
問題を解いたり解説を読んだりしているときに，項数の話をしているのか，項の値の話をしているのか，見失わないように，慎重に進めていきましょう。
また，群ごとの様子を把握しやすいように，表にまとめて考えるのがおすすめです。
群数列は苦手な人がとても多い分野です。この記事を参考にして，周りに差をつけていきましょう！
群数列と並び，数列の苦手ポイント二大巨頭の一角ともいえる「漸化式」についても説明しているので，ぜひ読んでみてくださいね。
このブログでは，自分で勉強しているとき，つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や，勉強が楽しくなる文房具も紹介していますので，よろしければご覧ください！
コメント