学生の方
学生の方2次関数の最大最小で、場合分けがあるやつのやり方が全然わかんないんだよね…
2次関数の最大値や最小値は、グラフを描いて求めることになりますが、式や定義域にaなどの文字が入ってると、急に難しくなりますよね。
「場合分け」が苦手な人にとっては大きなつまずきポイントになってしまいます。
実は、2次関数の最大値や最小値を求める問題には、決まった形があります。
その形を覚えて、それに従って場合分けを作っていけば、簡単に解けるようになります。
この記事では、場合分けが必要な2次関数の最大最小問題の解き方をわかりやすく解説していきます。
これを読めば、2次関数の場合分けは怖くない!どころか二次関数が範囲の定期テストは高得点も夢じゃない!

粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

2次関数が最大・最小になるのは3か所だけ!
2次関数のグラフは放物線なので、定義域がどんなふうになっても、最大値や最小値を取る可能性のある場所は次の3か所だけです。
- 範囲の左端
- 頂点
- 範囲の右端
問題によっては2つになる場合もありますが、とにかく場合分けは最大で3つということであることを覚えておきましょう。
この「覚える」ということが意外と大切なんです。
2次関数の最大最小(式に文字がある場合)
これを踏まえた上で、こんな問題をやってみましょう。
2次関数y=x^2-ax+2の、0\leqq x\leqq 1における最大値と最小値を求めよ。
とりあえず最大最小の問題はグラフを描かないと始まらないので、グラフを描きましょう。
まず、x^2の係数は正なので、下に凸のグラフということはわかります。
そして軸と頂点を求めるために、平方完成をします。
平方完成について詳しくはこちらの記事をご覧ください。
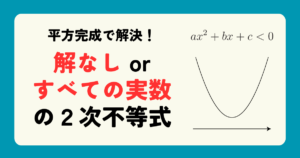
y=x^2-ax+2=\left(x-\cfrac{a}{2}\right)^2-\cfrac{a^2}{4}+2ということで軸はx=\cfrac{a}{2},頂点は\left(\cfrac{a}{2},-\cfrac{a^2}{4}+2\right)
グラフはこんな感じですね。

 粗茶さん
粗茶さん文字が入ってて具体的な値はわからないので、x軸やy軸はかかなくてOK。
まずは最小値からやっていきますよ。
最小値は、軸が定義域内にあるかないかで分ける
下に凸のグラフの場合、最小値は、「範囲の左端」「頂点」「範囲の右端」の3か所でとります。
なので、場合分けも3通りになります。
範囲の左端で最小になる場合
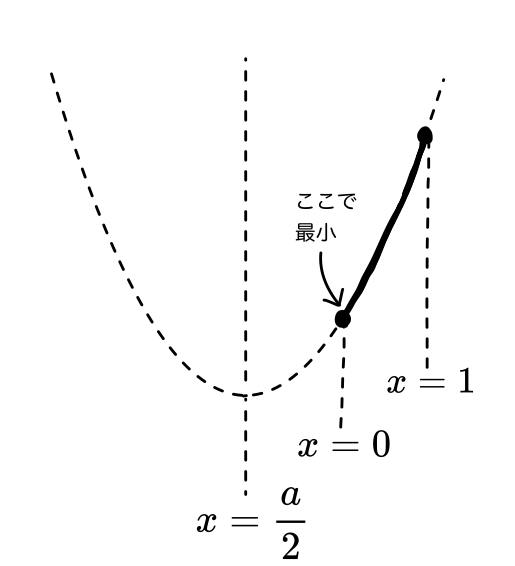
グラフから、\cfrac{a}{2}は0よりも左になります。
ので、aの範囲は
\cfrac{a}{2}<0 \therefore \color{red}a<0となります。
頂点で最小になる場合
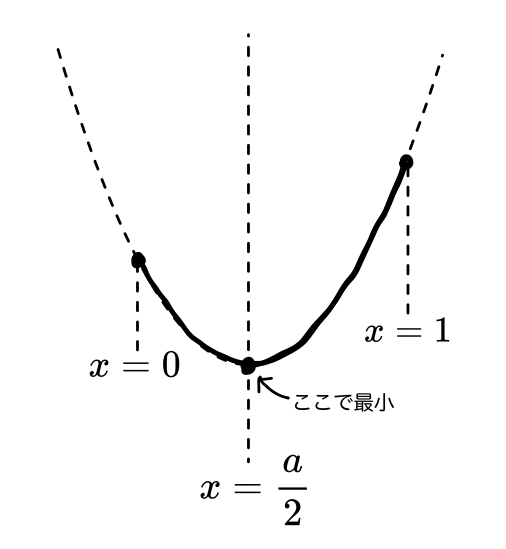
グラフから、\cfrac{a}{2}は0と1の間にあるので、
aの範囲は
0\leqq \cfrac{a}{2}<1 \therefore \color{red}0\leqq a <2となります。
 粗茶さん
粗茶さん上の図だと右側のほうが高くなっていますが、いまは最小値に注目しているので、左側を高く書いてもどちらでもOK。
範囲の右端で最小になる場合
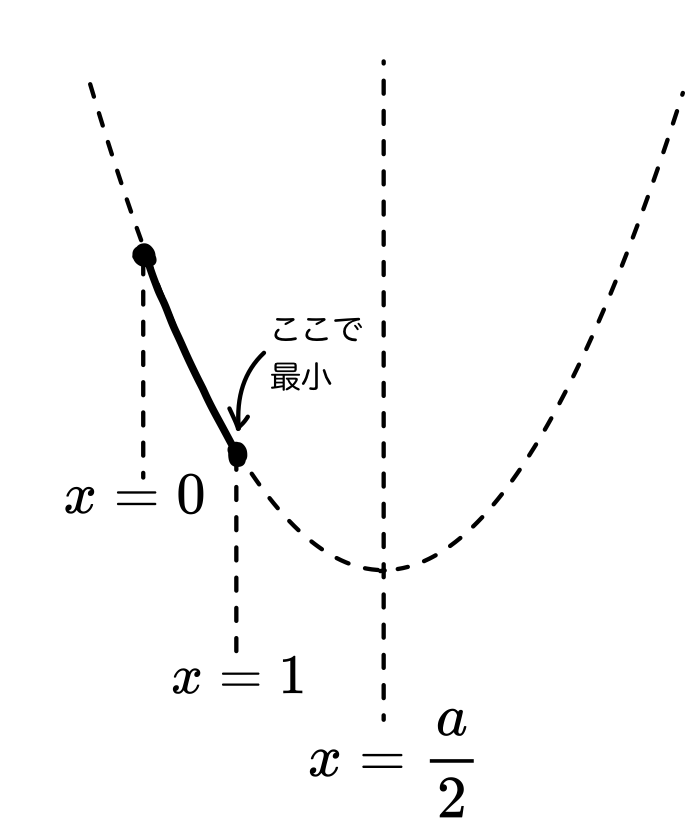
グラフから、\cfrac{a}{2} は 1よりも右になります。
ので、a の範囲は
1\leqq\cfrac{a}{2} \therefore \color{red}2\leqq a以上から、最小値については、
\begin{array}{ll}
[1]&a<0\\\\
[2]&0\leqq a<2\\\\
[3]&2\leqq a
\end{array}の3通りに場合分けします。
それでは解答です。
(解答)
y=x^2-ax+2=\left(x-\cfrac{a}{2}\right)^2-\cfrac{a^2}{4}+2[1] a<0のとき
x=0で最小値
0^2-a\cdot 0+2=2
 粗茶さん
粗茶さん平方完成する前の式のxに0を代入しました。

[2] 0\leqq a<2のとき
x=\cfrac{a}{2}で最小値
-\cfrac{a^2}{4}+2 粗茶さん
粗茶さん頂点のy座標なので、計算しなくてもOK

[3] 2\leqq aのとき
x=2で最小値
2^2-a\cdot 2+2=4-2a
 粗茶さん
粗茶さん平方完成する前の式のxに2を代入しました。

ここまでで、最小値は完了
不等号にイコールをつけるかつけないか問題
 学生の方
学生の方場合分けの作りかたはわかったんだけど、不等号にイコールがついてたりついてなかったりするのはどういうこと?
不等号のイコールについては、場合分けの分かれ目になっている数(今回は0と2)がどこかに含まれていれば、どこにつけてもOKです。
許容されるパターンをいくつか挙げておきましょう。
OK例①
\begin{array}{ll}
[1]&a<0\\\\
[2]&0\leqq a <2\\\\
[3]&2\leqq a
\end{array}0は[2]に、2は[3]に含まれる。
OK例②
\begin{array}{ll}
[1]&a\leqq 0\\\\
[2]&0< a \leqq2\\\\
[3]& 2< a
\end{array}0は[1]に、2は[2]に含まれる。
OK例③
\begin{array}{ll}
[1]&a<0\\\\
[2]&0\leqq a\leqq 2\\\\
[3]&2< a
\end{array}0と2は両方とも[2]に含まれる。
一方、0や2がどの場合にも含まれないような書き方はNGとなります。
NG例①
\begin{array}{ll}
[1]&a<0\\\\
[2]&0< a \leqq2\\\\
[3]&2\leqq a
\end{array}0がどこにも含まれない。
NG例②
\begin{array}{ll}
[1]&a\leqq 0\\\\
[2]&0\leqq a<2\\\\
[3]& 2< a
\end{array}2がどこにも含まれない。
NG例③
\begin{array}{ll}
[1]&a<0\\\\
[2]&0< a< 2\\\\
[3]&2< a
\end{array}0と2の両方がどこにも含まれない。
 粗茶さん
粗茶さん考えるのがめんどくさい…という人は、すべての不等号にイコールをつけておくっていうのも、悪くはないです。
最大値は「範囲の中心」と「軸」の位置関係で場合分け。
続いて最大値について。
下に凸のグラフでは、頂点が最も下にくるので、頂点で最大値をとることはできません。
よって、最大値は、「範囲の右端」でとる場合と「範囲の左端」でとる場合があります。
場合分けは2通りです。
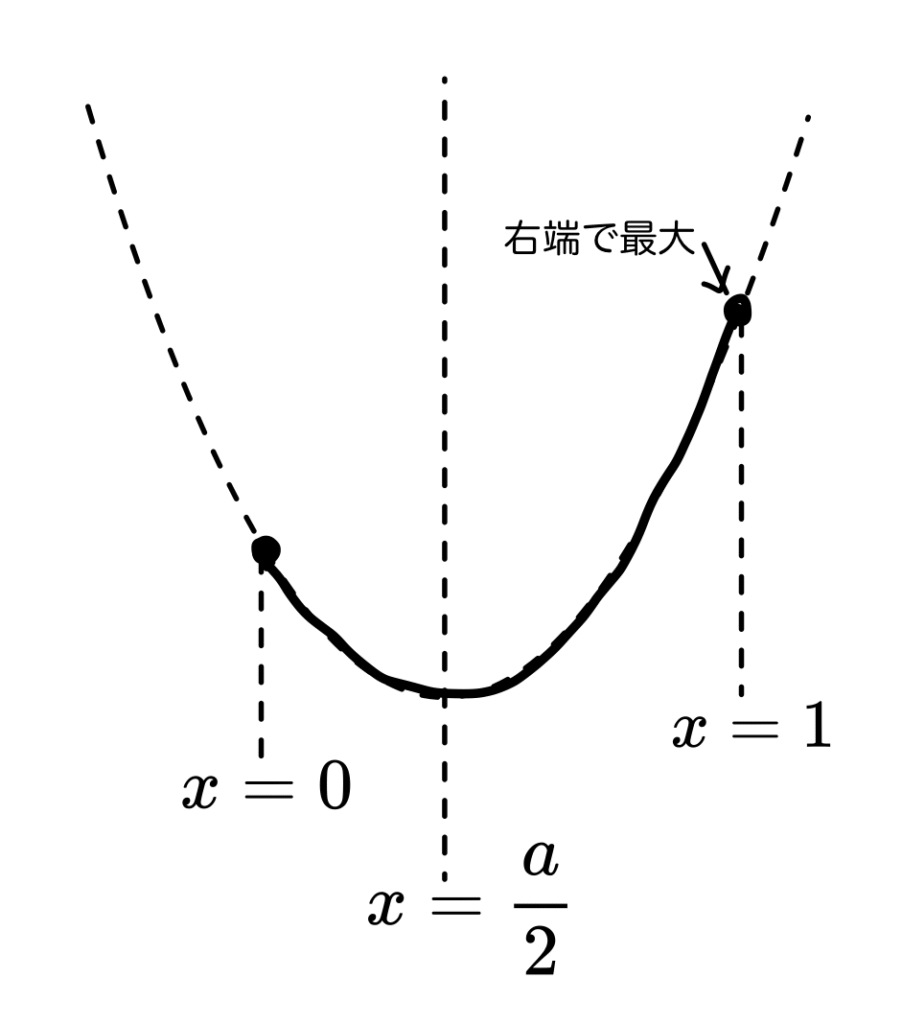
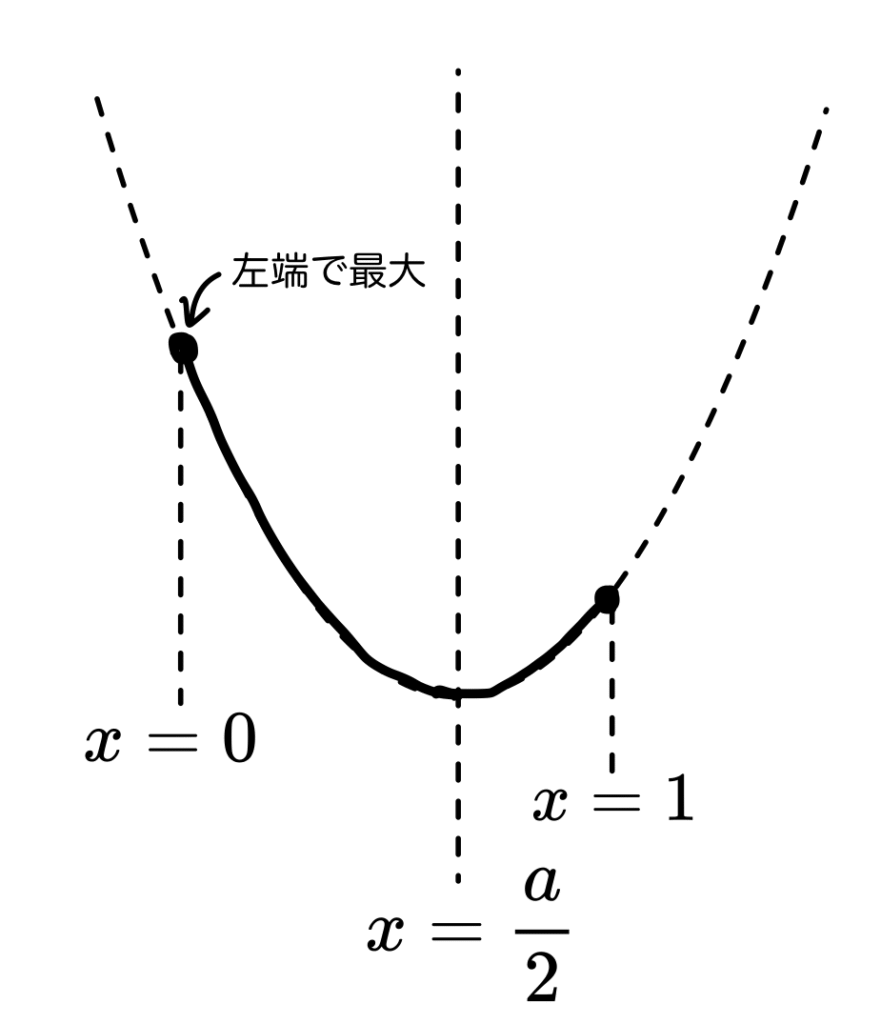
問題は、この2つがどこで分かれるか?ということ。
ヒントは放物線が左右対称な形をしているという事実です。
aの値によっては、左端と右端が同じ高さになることもありそうですよね。
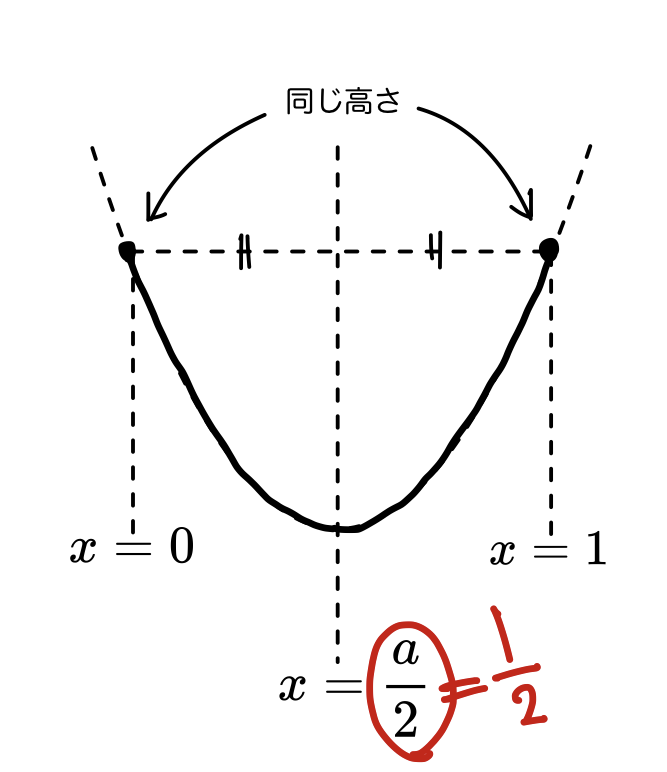
このとき、次の図の太線の部分は左右対称。
ということは、軸の\cfrac{a}{2}は、0と1の真ん中の\cfrac{1}{2}と一致します。
そして、軸の\cfrac{a}{2}が\cfrac{1}{2}からすこしでもずれると、左端か右端のどちらかが高くなって、最大値を取る場所が決まります。
つまり、下に凸のグラフの最大値については「範囲の中央」と「軸」の位置関係で場合分けをします。
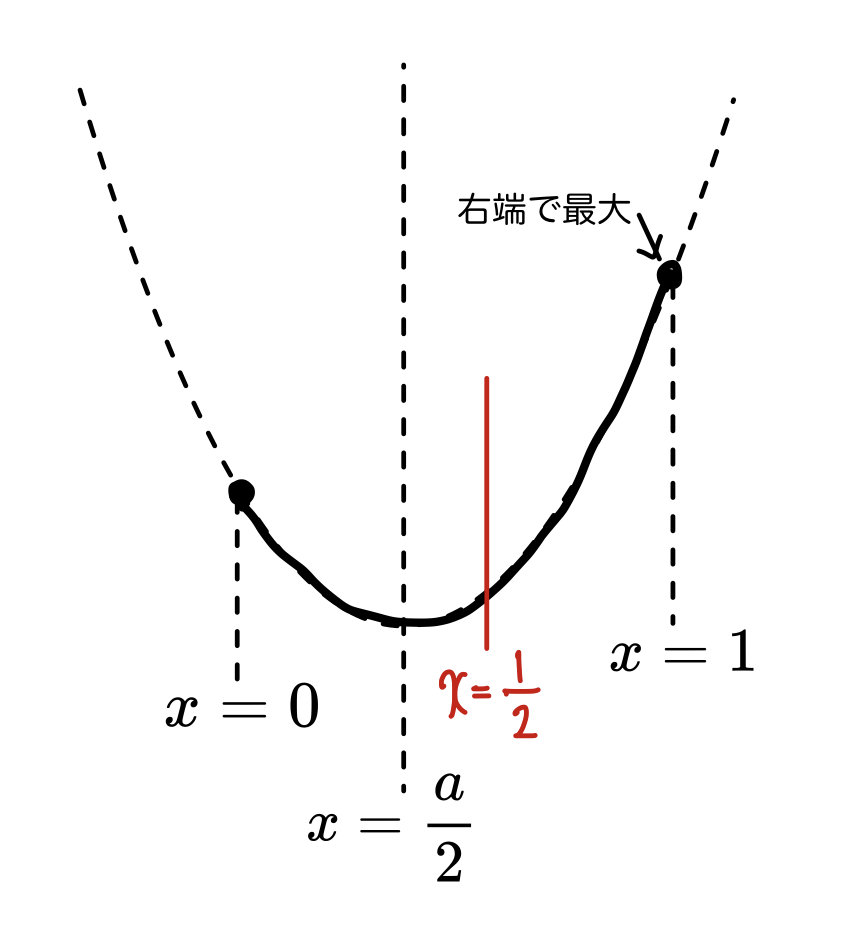
範囲の右端で最大の場合

この場合、軸\cfrac{a}{2}は範囲の中央\cfrac{1}{2}より左にあるので、aの範囲は
\cfrac{a}{2}<\cfrac{1}{2} \therefore \color{red}a<1範囲の左端で最大の場合
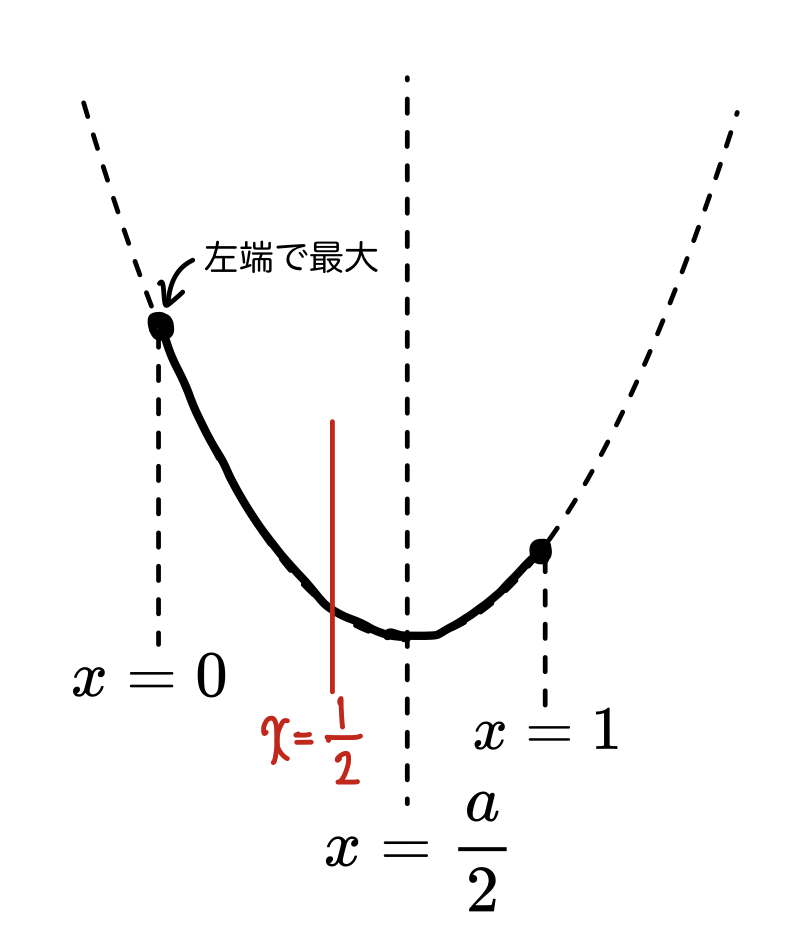
この場合、軸\cfrac{a}{2}は範囲の中央\cfrac{1}{2}より右にあるので、aの範囲は
\cfrac{1}{2}\leqq \cfrac{a}{2} \therefore \color{red}1\leqq a以上から、最大値については、
\begin{array}{ll}
[1]&a<1\\\\
[2]&1\leqq a
\end{array}の2通りに場合分けします。
 粗茶さん
粗茶さん最小値のときと同様で、不等号のイコールはどちらかについてればOK。
それでは解答です。
(解答)
y=x^2-ax+2=\left(x-\cfrac{a}{2}\right)^2-\cfrac{a^2}{4}+2[1] a<1のとき
x=1で最大値
1^2-a\cdot 1+2=3-a
 粗茶さん
粗茶さん平方完成する前の式のxに1を代入しました。
[2] 1\leqq aのとき
x=0で最大値
0^2-a\cdot 0+2=2
 粗茶さん
粗茶さん平方完成する前の式のxに0を代入しました。

これで完了です。
もう1つ別の問題を。
2次関数の最大最小(範囲に文字がある場合)
2次関数y=x^2-4x+1の、a\leqq x\leqq a+1における最大値と最小値を求めよ。
範囲の方にaがついています。
教科書などでは、式にaが入っている問題を分けて扱われていますが、やり方は同じです。
まずはグラフを描くために平方完成。
y=x^2-4x+1=(x-2)^2-3
なので頂点は(2,-3)です。
最小値の場合分け
下に凸なので、最小値は、「範囲の左端」「頂点」「範囲の右端」の3通り。

このとき
a+1<2\Leftrightarrow a<1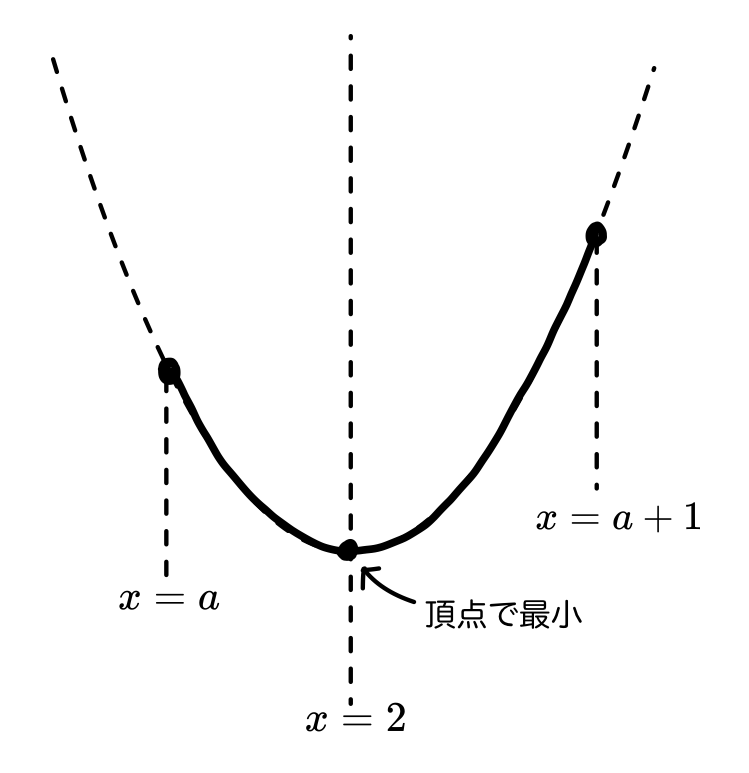
このとき
a\leqq 2 <a+1 \Leftrightarrow 1<a\leqq 2
このとき
2<aこれをもとに最小値を求めます。
(解答)
y=x^2-4x+1=(x-2)^2-3
[1] a<1のとき
x=a+1で最小値
(a+1-2)^2-3=a^2-2a-2
 粗茶さん
粗茶さん平方完成後の式に代入してみました。

[2] 1< a\leqq 2のとき
x=2で最小値-3
 粗茶さん
粗茶さん頂点のy座標です。

[3] 2<aのとき
x=aで最小値
a^2-4a+1

最大値の場合分け
下に凸なので、最大値は2通り。範囲の中央a+\cfrac{1}{2}と軸2の大小関係です。
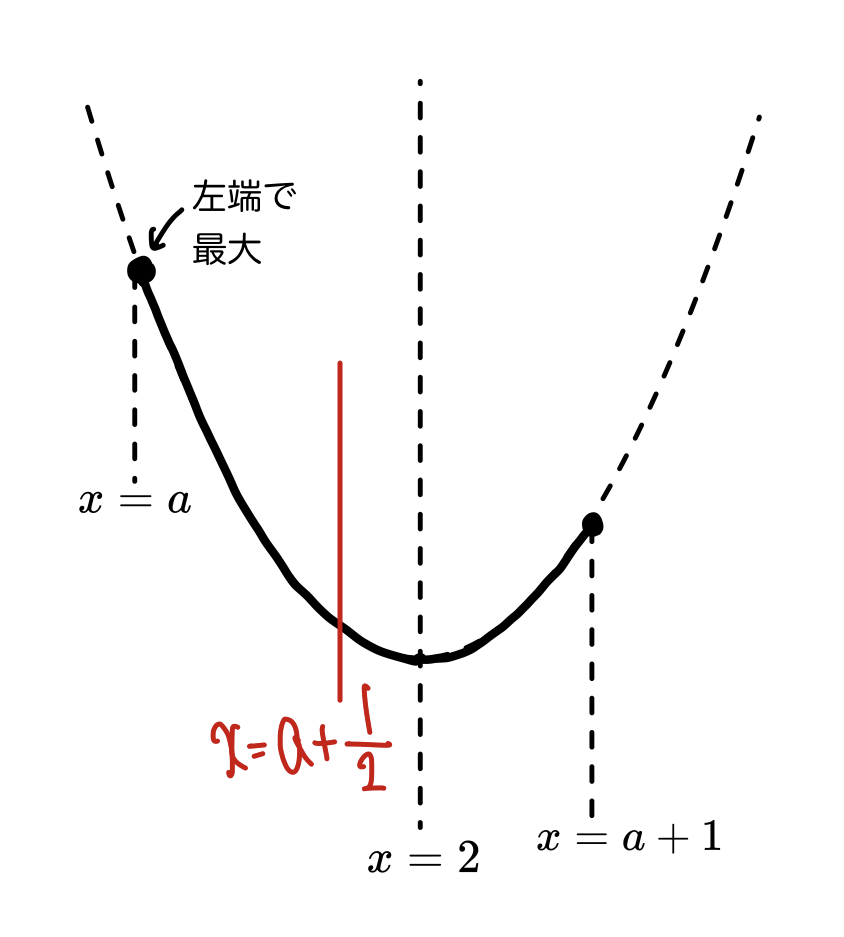
このときa+\cfrac{1}{2}<2
\Leftrightarrow a<\cfrac{3}{2}
このとき2\leqq a+\cfrac{1}{2}
\Leftrightarrow \cfrac{3}{2}\leqq a(解答)
y=x^2-4x+1=(x-2)^2-3
[1] a<\cfrac{3}{2}のとき
x=aで最大値
a^2-4a+1

[2] \cfrac{3}{2}\leqq aのとき
x=a+1で最大値-3
(a+1-2)^2-3=a^2-2a-2
 粗茶さん
粗茶さんどちらも最小値の計算のときに出てきましたね。

まとめ
2次関数の最大・最小問題における場合分けは、高校数学で最初に乗り越えなければならない壁かもしれません。
場合分けは、最初から式(a<0など)を作ることはほぼ不可能なので、実現される図のパターンを描き出して、それぞれにあてはまるaの範囲を作るという手順で進めましょう。
特に、2次関数については形が決まっていて、「範囲の左端」「頂点」「範囲の右端」の3か所でしか最大や最小にならないことを覚えておくと有利です。
最初は少し難しく感じるかもしれませんが、パターンを丁寧に整理していけば、必ず自分の力になります。
焦らず一歩ずつ、頑張っていきましょう!
このブログでは,自分で勉強しているとき,つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や,勉強が楽しくなる文房具も紹介していますので,よろしければご覧ください!