 学生の方
学生の方方程式や不等式に絶対値が入っていると,突然難しくなるよね…
絶対値を含む方程式・不等式の解き方で悩んでいませんか?
実は,絶対値の方程式・不等式は,やり方を覚えれば決して難しい問題ではありません。
なぜなら絶対値の場合分けや,方程式・不等式の形はほとんど決まっているからです。
この記事では,絶対値を含む方程式・不等式の攻略法を,式のパターン別にわかりやすく説明します。
この記事を読めば,式に絶対値が出てきても恐れることはなくなります。
絶対値の方程式・不等式を得意分野にして,友達と差をつけちゃいましょう!
- 絶対値を含む方程式・不等式の解き方がわかる
絶対値のはずしかたについては,以下の記事もお読みください。


粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

絶対値の方程式・不等式は場合分け…とは限らない。
 学生の方
学生の方絶対値の方程式と不等式って,毎回場合分けしなきゃいけないから大変…
絶対値といえば,必ず「場合分け」が必要だと思っていませんか?
実は,方程式・不等式によっては,場合分けをしなくても解ける場合があります。
見分ける基準は,「絶対値の個数」と「絶対値の外にxがあるかどうか」の2点。
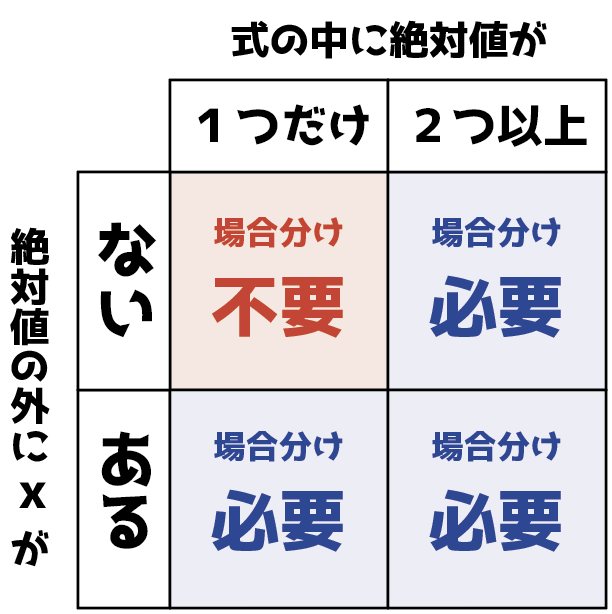
方程式・不等式の中に絶対値が1つだけで,かつ,絶対値の外にxがないとき,場合分け不要で解くことができます。
- |x|=5
- |3x+2|<8
- |2x|+3\geqq 0
絶対値記号が1つであればいいので,絶対値の中身はどんな式であっても大丈夫です。
一方,方程式・不等式の中に絶対値が2つ以上あるか,または,絶対値の外にxがあるときは,必ず場合分けをします。
- |x+2|-|x-3|=5(絶対値が2つ)
- |3x+2|<x+8(絶対値の外にもxがある)
- |2x|+|5-3x|-|x^2+4x-3|-x^2+7x\geqq 0(絶対値が2つ以上で,かつ,絶対値の外にもxがある)
それぞれの場合について,方程式と不等式の解き方を解説していきます。
絶対値の方程式・不等式:場合分けが不要なもの
絶対値の方程式・不等式のうち,絶対値が1つだけで,絶対値の外にxがない場合は,場合分けが不要です。
次の方程式・不等式を解け。
(1)|x|=5
(2)|x|<4
(3)|x|>2
絶対値の定義である「距離」の考え方で解けますよ。
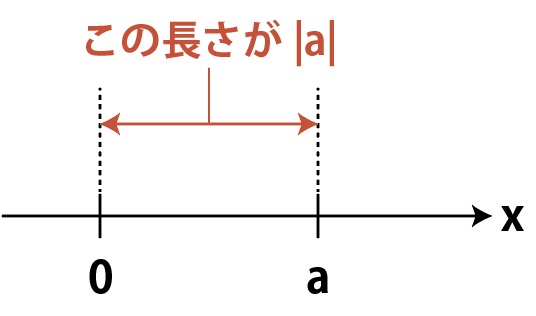
数直前上で原点(0)から,ある実数aまでの距離を「aの絶対値」といい,
\LARGE{|a|}と書く。
(1)
|x|=5は,「0からxまでの距離が5」という意味。
図にするとこうなります。
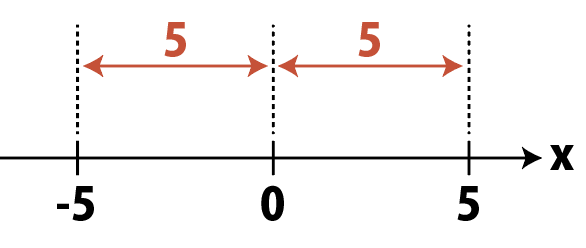
0からの距離が5になるようなxは5と-5なので,答えは,
x=\pm 5 …(答)
(2)
|x|<4は,「0からxまでの距離が4より小さい」という意味。
図にするとこうなります。
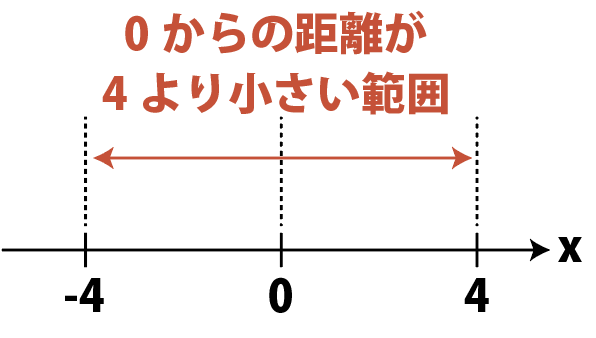
0からの距離が4より小さくなるようなxの範囲は,4と-4の間なので,答えは,
-4<x<4 …(答)
(3)
|x|>2は,「0からxまでの距離が2より大きい」という意味。
図にするとこうなります。
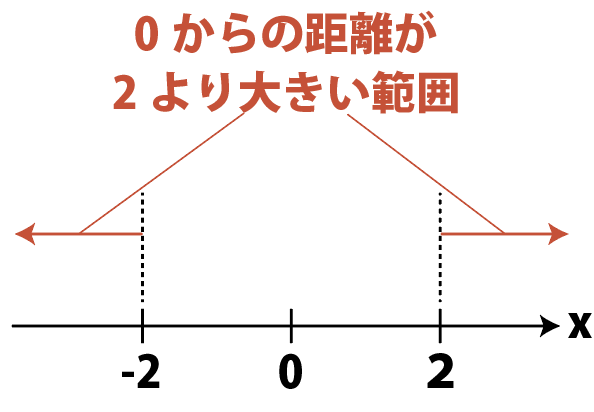
0からの距離が2より大きくなるようなxの範囲は,-2より左の範囲と,2より右の範囲なので,答えは,
x<-2,2<x …(答)
「絶対値」=「距離」という考え方を使えば,場合分けなしで方程式や不等式を解くことができます。
一応,公式になっているので,まとめておきます。
xを実数,aを0以上の定数とする。
\begin{aligned}
|x|=a& \Leftrightarrow x=\pm a\\\\
|x|< a& \Leftrightarrow -a < x < a\\\\
|x|> a& \Leftrightarrow x<-a,a< x
\end{aligned}公式は覚えていいのですが,いつも数直線のイメージすると考えやすいです。
次の方程式・不等式を解け。
(1)|x-2|=5
(2)|x+3|<4
(3)|2x-5|>2
絶対値の中身が多項式になっている場合も考え方は同じ。公式のxのところを置き換えればOK。
(1)公式のxのかわりにx-2にします。
\begin{aligned}
& |x-2|=5\\\\
&\Leftrightarrow x-2=\pm 5\\\\
&\Leftrightarrow x=2\pm 5\\\\
&\Leftrightarrow x=7,-3 \cdots(答)
\end{aligned}(2)公式のxのかわりにx+3にします。
\begin{aligned}
& |x+3|<4\\\\
&\Leftrightarrow -4< x+3 < 4 \\\\
&\Leftrightarrow -7< x < 1 \cdots(答)
\end{aligned}(3)公式のxのかわりに2x-5にします。
\begin{aligned}
& |2x-5|>2\\\\
&\Leftrightarrow 2x-5<-2,2<2x-5 \\\\
&\Leftrightarrow 2x<3,7<2x \\\\
&\Leftrightarrow x <\cfrac{3}{2},\cfrac{7}{2} < x \cdots(答)
\end{aligned}絶対値の方程式・不等式:場合分けが必要なもの
絶対値の方程式・不等式は,多くの問題で,場合分けが必要です。
絶対値の場合分けは,中身の符号が0以上か負かで分けるんでしたね。
aを実数とする。
|a|=\begin{aligned}
\left\{
\begin{array}{l}
a&(a\geqq 0のとき)\\\\
-a&(a<0のとき)
\end{array}
\right.
\end{aligned}絶対値の方程式や不等式を解くときには,絶対値の部分を場合分けして,それぞれの場合について式を解いていきます。
次の方程式・不等式を解け。
(1)|x-2|=5
(2)|x+3|<4
 学生の方
学生の方これ,さっきの例題2と同じ問題じゃん!
場合分け不要!と紹介した形の方程式や不等式も,場合分けで解くことは可能です。
同じ問題ですが,今度は場合分けする方法で解いてみます。
(1)
|x-2|=\left\{\begin{array}{l}x-2&(x\geqq 2のとき)\\\\
-(x-2)&(x<2のとき)
\end{array}
\right.と場合分けできる。
(ⅰ)x\geqq 2のとき
\begin{array}{l}|x-2|=5\\\\
x-2=5\\\\
\therefore x=7
\end{array}これはx\geqq 2を満たす。
 粗茶さん
粗茶さん出てきた答えが場合分けの範囲x\geqq 2を満たしているか必ず確認しましょう。
(ⅱ)x<2のとき
\begin{array}{l}|x-2|=5\\\\
-(x-2)=5\\\\
-x+2=5\\\\
\therefore x=-3
\end{array}これはx<2を満たす。
以上(ⅰ)(ⅱ)より,
x=7,-3 \cdots(答)
 粗茶さん
粗茶さん当たり前ですが,例題2と同じ答えです。
(2)
|x+3|=\left\{\begin{array}{l}x+3&(x\geqq -3のとき)\\\\
-(x+3)&(x<-3のとき)
\end{array}
\right.と場合分けできる。
(ⅰ)x\geqq -3のとき
\begin{array}{l}|x+3|<4\\\\
x+3<4\\\\
\therefore x<1
\end{array} 粗茶さん
粗茶さん不等式の場合は,出てきた答えと,場合分けの範囲との共通部分を答えます。
これと,x\geqq -3(場合分けの範囲)との共通部分は,
-3\leqq x < 1
(ⅱ)x < -3のとき
\begin{array}{l}|x+3|<4\\\\
-(x+3)<4\\\\
-x-3<4\\\\
\therefore x>-7
\end{array}これと,x < -3(場合分けの範囲)との共通部分は,
-7 < x <-3
(ⅰ)または(ⅱ)より,求める解は,
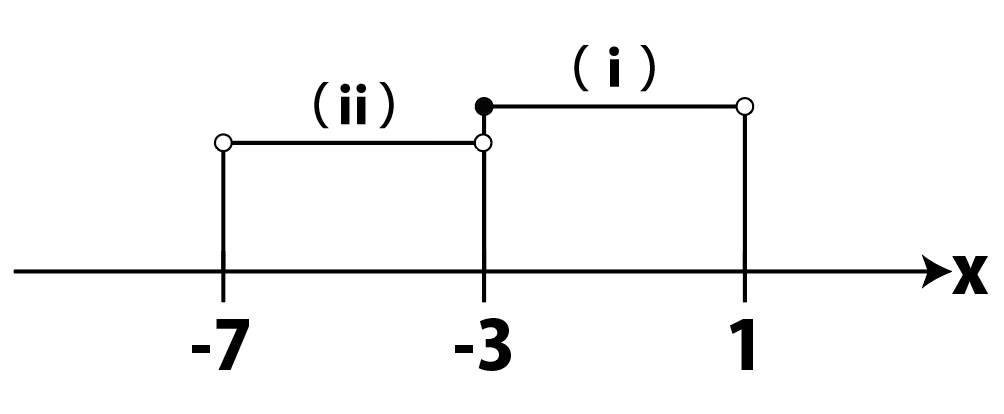
-7 < x < 1\cdots(答)
このようにして,場合分けで解くこともできます。
方程式の場合は,出てきた答えが場合分けの範囲に当てはまっているかどうか確認。
不等式の場合は,出てきた答えと場合分けの範囲との共通部分を答える。
ことに注意しましょう。
次の方程式・不等式を解け。
(1)x^2-|2x-1|-3=0
(2)|x+3|+|2x-1|=5
(3)|x-2|-|3x+2|\geqq 2
すべて場合分けで解くしかないパターンです。
(1)
|2x-1|=
\left\{
\begin{array}{l}
2x-1&\left(x\geqq\cfrac{1}{2}のとき\right)\\\\
-(2x-1)&\left(x<\cfrac{1}{2}のとき\right)
\end{array}
\right.と場合分けできる。
(ⅰ)x\geqq \cfrac{1}{2}のとき
\begin{array}{rcl}
x^2-(2x-1)-3&=&0\\\\
x^2-2x-2&=&0\\\\
\therefore x&=&1\pm\sqrt{3}
\end{array} 粗茶さん
粗茶さん場合分けの範囲に当てはまっているかを確認しましょう。
ここで,x=1-\sqrt{3}は,x\geqq\cfrac{1}{2}を満たさないので不適。
したがって,
x=1+\sqrt{3}
(ⅱ)x<\cfrac{1}{2}のとき
\begin{array}{rcl}
x^2-\{-(2x-1)\}-3&=&0\\\\
x^2+2x-4&=&0\\\\
\therefore x&=&1\pm\sqrt{5}
\end{array}ここで,x=1+\sqrt{5}は,x<\cfrac{1}{2}を満たさないので不適。
したがって,
x=1-\sqrt{5}
以上(ⅰ)(ⅱ)より,
x=1+\sqrt{3},1-\sqrt{5} \cdots(答)(2)2つの絶対値があるときは,それぞれを場合分けして,2つを合体させます。
|x+3|=\left\{\begin{array}{l}
x+3&(x\geqq-3のとき)\\\\
-(x+3)&(x<-3のとき)
\end{array}\right.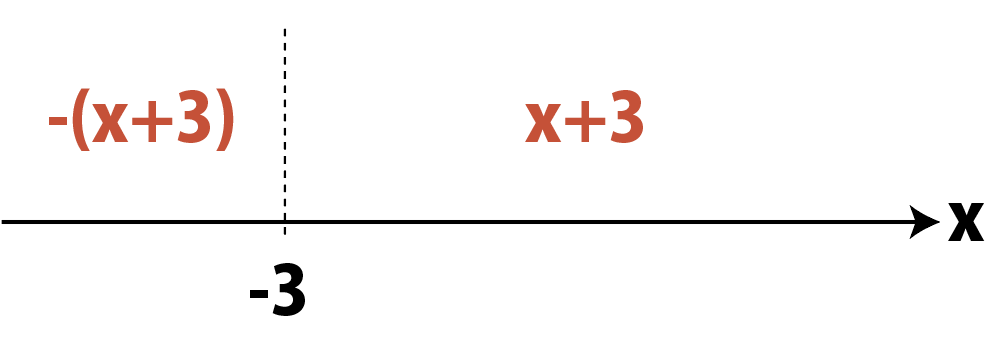
|2x-1|=\left\{\begin{array}{l}
2x-1&(x\geqq\cfrac{1}{2}のとき)\\\\
-(2x-1)&(x<\cfrac{1}{2}のとき)
\end{array}\right.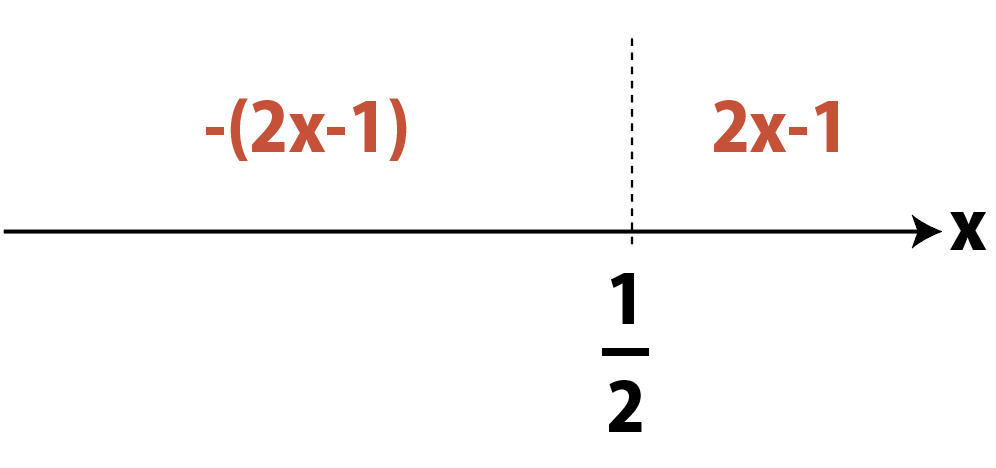
この2つを合体させて,
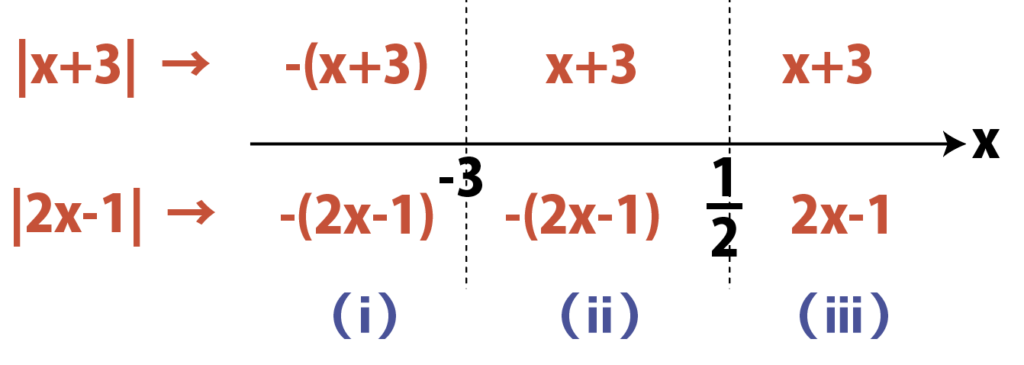
(ⅰ)x<-3のとき
\begin{array}{rcl}
-(x+3)+\{-(2x-1)\}&=&5\\\\
-3x-2&=&5\\\\
\therefore x&=&-\cfrac{7}{3}
\end{array}これは,x<-3を満たさず,不適。
(ⅱ)-3\leqq x <\cfrac{1}{2}のとき
\begin{array}{rcl}
(x+3)+\{-(2x-1)\}&=&5\\\\
-x+4&=&5\\\\
\therefore x&=&-1
\end{array}(これは-3\leqq x < \cfrac{1}{2}を満たす。)
(ⅲ)\cfrac{1}{2} \leqq xのとき
\begin{array}{rcl}
(x+3)+(2x-1)&=&5\\\\
3x+2&=&5\\\\
\therefore x&=&1
\end{array}(これは\cfrac{1}{2} \leqq xを満たす。)
以上(ⅰ)〜(ⅲ)より,
x=\pm 1 \cdots(答)
 粗茶さん
粗茶さんx=-1とx=1が適する答えだったので,まとめちゃいました。
(3)不等式になっても,場合分けは同じです。
|x-2|=\left\{\begin{array}{l}
x-2&(x\geqq2のとき)\\\\
-(x-2)&(x<2のとき)
\end{array}\right.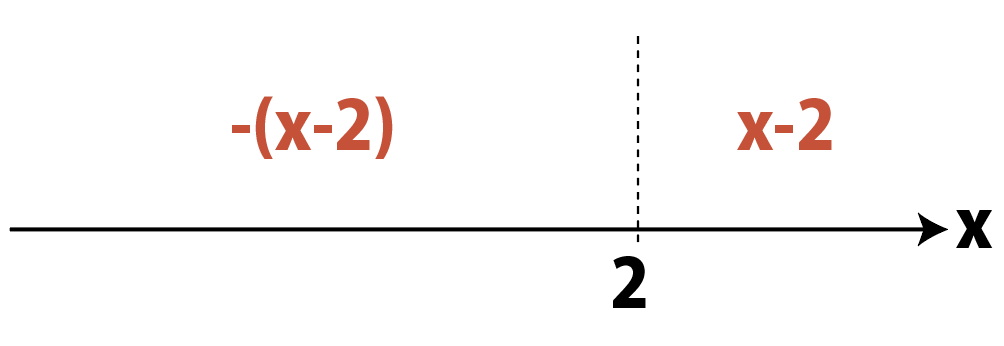
|3x+2|=\left\{\begin{array}{l}
3x+2&(x\geqq-\cfrac{2}{3}のとき)\\\\
-(3x+2)&(x<-\cfrac{2}{3}のとき)
\end{array}\right.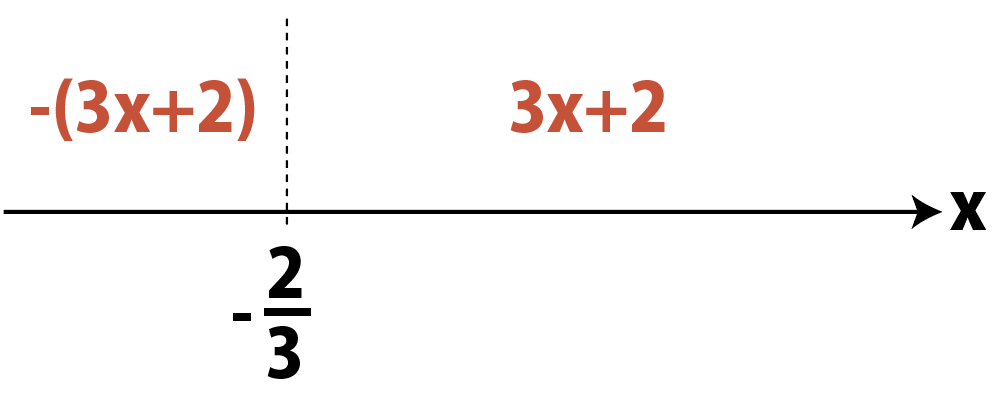
この2つを合体させて,
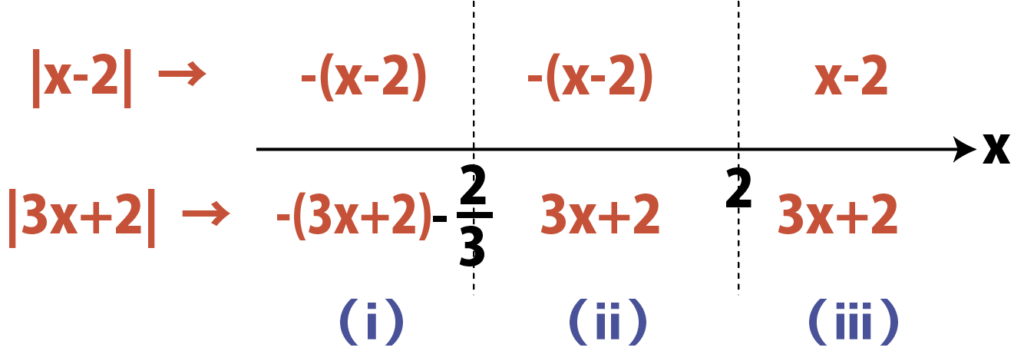
(ⅰ)x<-\cfrac{2}{3}のとき
\begin{array}{rcl}
-(x-2)-\{-(3x+2)\}&\geqq&2\\\\
2x+4&\geqq&2\\\\
\therefore x&\geqq&-1
\end{array}これと,x<-\cfrac{2}{3}の共通部分は,
-1\leqq x<-\cfrac{2}{3}
(ⅱ)-\cfrac{2}{3}\leqq x <2のとき
\begin{array}{rcl}
-(x-2)-(3x+2)&\geqq&2\\\\
-4x&\geqq&2\\\\
\therefore x&\leqq&-\cfrac{1}{2}
\end{array}これと,-\cfrac{2}{3}\leqq x <2の共通部分は,
-\cfrac{2}{3}\leqq x \leqq -\cfrac{1}{2}
(ⅲ)2\leqq xのとき
\begin{array}{rcl}
(x-2)-(3x+2)&\geqq&2\\\\
-2x-4&\geqq&2\\\\
\therefore x&\leqq&-3
\end{array}これと2\leqq xの共通部分は存在しない。
(ⅰ)または(ⅱ)または(ⅲ)より,
-1\leqq x\leqq -\cfrac{1}{2} \cdots(答) 粗茶さん
粗茶さん場合分けの範囲との共通部分をそれぞれ求めて,最後に足し合わせます。
絶対値の数が増えると,場合分けの数も増えるので,手間が多くなりますが,基本的な解き方は変わりません。
・方程式→出てきた答えが場合分けの範囲を満たすかを確認
・不等式→出てきた答えと場合分けの範囲の共通部分を答えにする
これらを徹底しましょう。
まとめ:解き方の形を身につけよう
この記事では,絶対値を含む方程式・不等式の解き方を紹介しました。
今回の内容をおさらいしましょう。
- 絶対値が1つだけで,かつ,絶対値の外にxがない→場合分け不要
- 絶対値が2つ以上または絶対値の外にxがある→場合分けする
- 方程式→出てきた答えが場合分けの範囲を満たすかを確認
- 不等式→出てきた答えと場合分けの範囲の共通部分を答えにする
場合分けが必要なときでも,分けることができれば,それぞれの計算自体は難しくないはずです。
それぞれの計算結果が場合分けの範囲に含まれているかも,必ず確認しましょう。
このブログでは,自分で勉強しているとき,つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や,勉強が楽しくなる文房具も紹介していますので,よろしければご覧ください!



