 学生の方
学生の方「直線の通過領域を図示せよ」っていう問題が出たんだけど、やったことないから全く手がつけられなかった。
大学入試の勉強をしていると、直線の通過領域を求める問題に出会うことがあります。
ですが、学校の教科書や授業ではあまり触れられていないので、突然問題に出されて手がつけられなかった経験はありませんか?
この記事では、図形と方程式の「直線の通貨領域」の問題を、2通りのアプローチで解説。
解法にいたるまでの考え方も含めてわかりやすく説明していきます。
入試で頻出の問題ながらできる人が少ないところでもあるので、得点源にしていきたいですね!
「直線の通過領域」を求める問題の、2通りの解き方と考え方がわかる。

粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

通過領域の問題の解き方
それでは,通過領域の問題を解いてみましょう。
直線y=ax+a^2…①について,aがすべての実数値をとって変化するとき,直線①が通過する領域を図示せよ。
通過領域の問題には,解き方が主に2種類あります。
- aの方程式にする
- 1文字を固定する
どちらの方法で解いても同じ答えになりますが、どちらの方法でも解けるようにしておくと応用がききます。
1つずつ説明していきます。
解き方① aの方程式にする
いきなり通過する領域といわれても難しいので、直線①はどの点を通過して、どの点を通過しないかを考えてみましょう。
考え方は次のようになります。
直線①に点(x,y)を代入してできるaの方程式が
- 実数解aが存在する→①は点(x,y)を通過する。
- 実数解aが存在しない→①は点(x,y)を通過しない。
具体的にやってみましょう。
①にx=0,y=1を代入すると,
\begin{array}{ll}
&1=a\cdot 0+a^2\\\\
\Leftrightarrow&a^2=1\\\\
\therefore&a=\pm 1
\end{array}で,実数aは存在するので,①は点(0,1)を通過する。
続いて,①にx=1,y=2を代入すると,
\begin{array}{ll}
&2=a\cdot 1+a^2\\\\
\Leftrightarrow&a^2+a-2=0\\\\
\therefore&a=\cfrac{-1\pm\sqrt{5}}{2}
\end{array}で,こちらも実数aが存在するので,①は点(1,2)も通過する。
続いて、x=-1,y=-2ではどうでしょうか?①に代入してみます。
\begin{array}{ll}
&-2=a\cdot(-1)+a^2\\\\
\Leftrightarrow&a^2-a+2=0\\\\
\therefore&a=\cfrac{1\pm\sqrt{-3}}{2}
\end{array}で,これは実数ではない。つまり実数aは存在しないので,直線①は点(-1,-2)を通過しない。
このように,直線の式に代入してみて,実数aが存在したときの点(x,y)を集めたものが,この直線の通過領域ということになります。
 学生の方
学生の方そんな点なんて無限にあるじゃん!
もちろん,すべての点を集めることは不可能です。
そこで少し視点を変えて,x,yがどんな時に実数aが存在するのか?を考えてみます。
①をaについて整理すると,
a^2+xa-y=0\cdots①'
という,aの二次方程式とみることができます。
そして,このaが実数になる,つまりaの方程式①’が実数解をもてばいいということ。
2次方程式が実数解を持つ条件といえば,判別式が0以上でしたので,①’の判別式をDとすると,
 粗茶さん
粗茶さんあ,ax^2+bx+c=0の判別式Dはb^2-4acね。
\begin{array}{lll}
D&=&x^2-4\cdot 1^2\cdot(-y)\\\\
&=&x^2+4y\geqq0\\\\
&\Leftrightarrow&y\geqq -\cfrac{1}{4}x^2
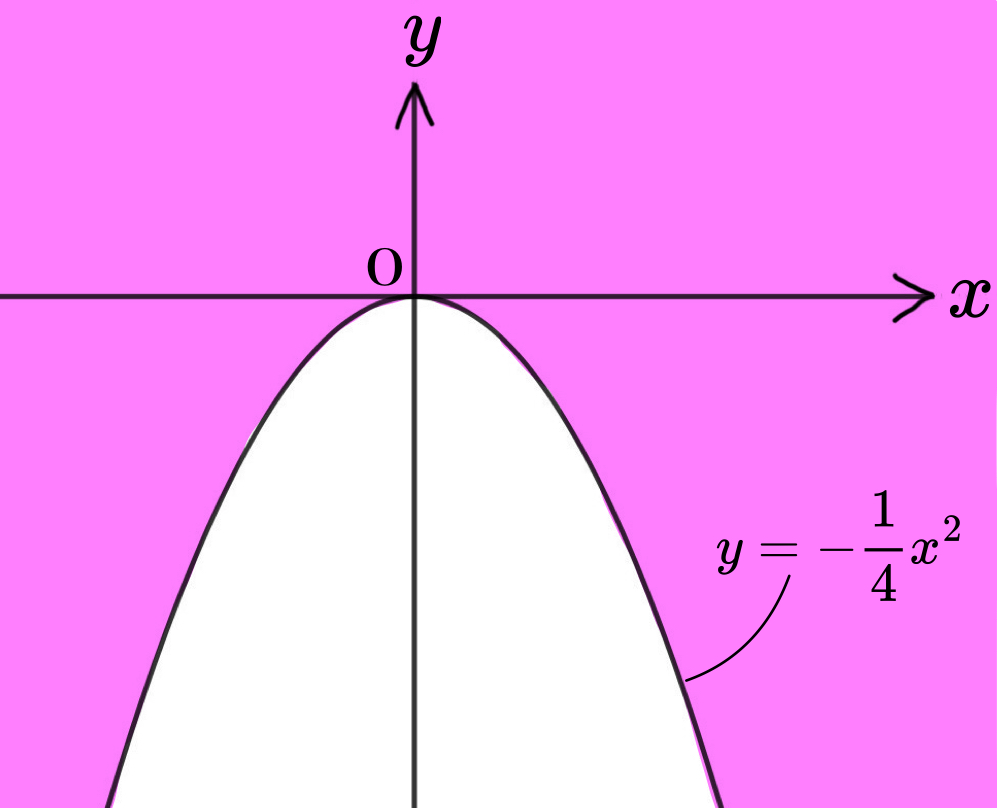
\end{array}(x,y)がこの不等式を満たすときに実数aは存在し,(x,y)は直線①の通過領域に含まれる。
ということで、求める通過領域は下図の色をつけた部分(境界を含む)。
解き方②xを固定する
通過領域の問題は、一つの文字(通常はx)を固定することで解く方法もあります。
同じ問題で考えてみます。
直線y=ax+a^2…①について,aがすべての実数値をとって変化するとき,直線①が通過する領域を図示せよ。
xをある数に固定したとき、yの範囲がどうなるかを考えてみます。
①にx=1を代入して、
\begin{array}{lll}
y&=&a\cdot 1+a^2\\\\
&=&\left(a+\cfrac{1}{2}\right)^2-\cfrac{1}{4}
\end{array}aはすべての実数をとるので、yの最小値は-\cfrac{1}{4}(最大値なし)
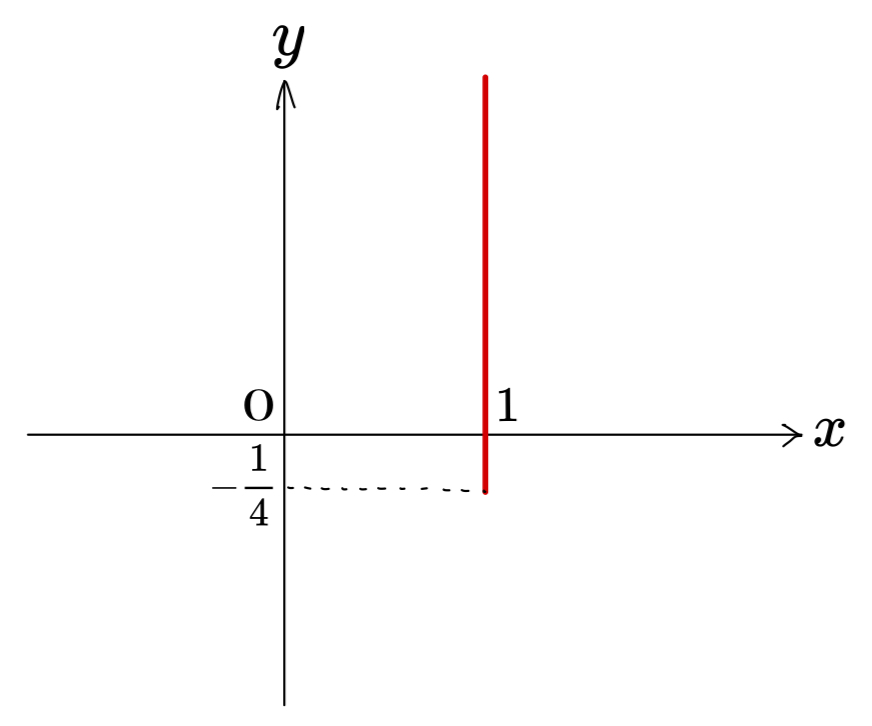
よって、x=1のときのyのとりうる範囲はy\geqq-\cfrac{1}{4}
よって、下図の赤線の部分は、直線①の通過領域に含まれる。
xに別の数字も代入してみましょう。
①にx=2を代入して、
\begin{array}{lll}
y&=&a\cdot 2+a^2\\\\
&=&\left(a+1\right)^2-1
\end{array}aはすべての実数をとるので、yの最小値は-1(最大値なし)
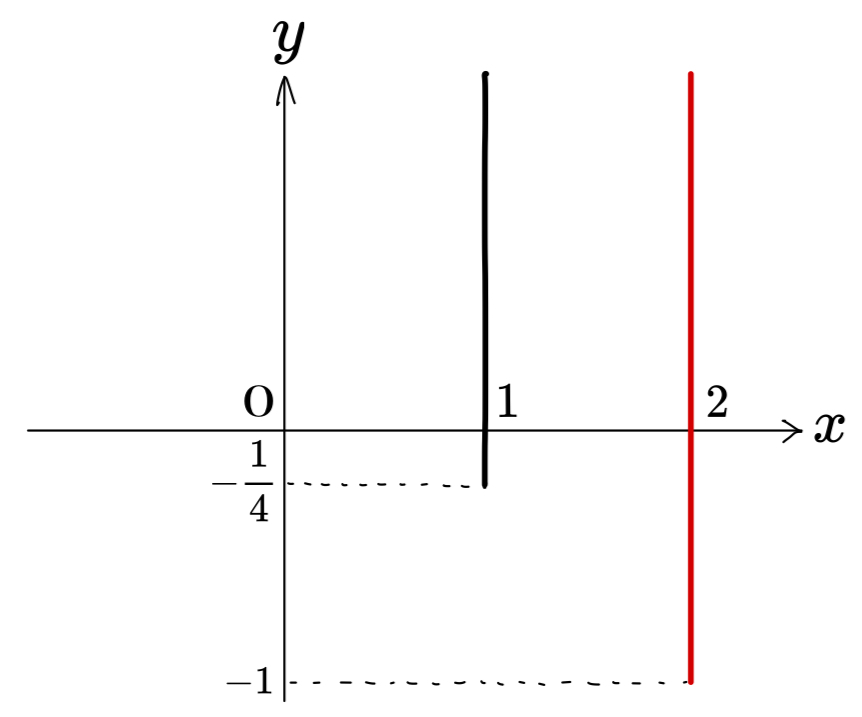
よって、x=2のときのyのとりうる範囲はy\geqq-1
よって、x=1のときに求めた部分に加えて、下図の赤線の部分も、直線①の通過領域に含まれる。
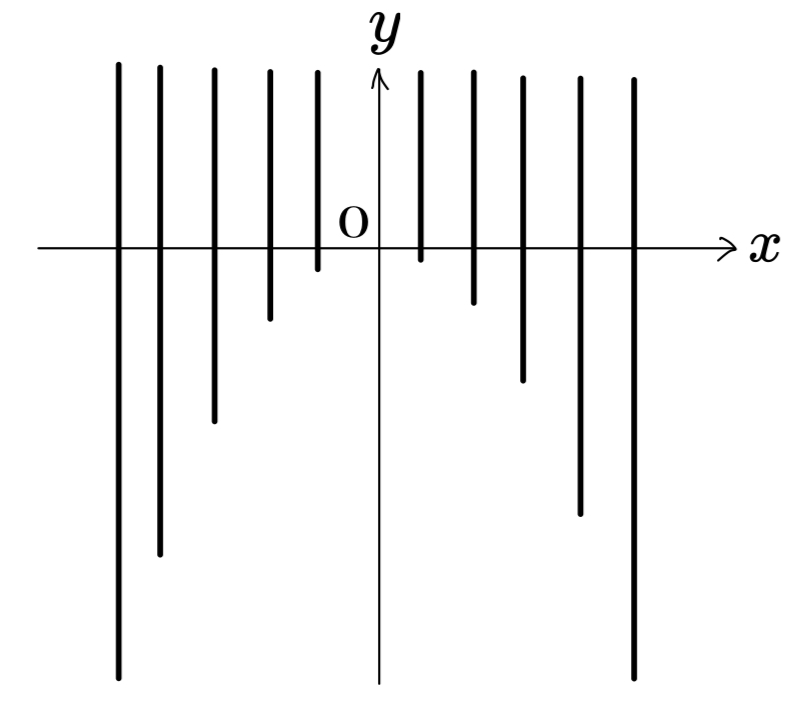
同様に、いろいろなxについて、yの取りうる範囲を求めて図に書き込んでいけば、直線①の通過領域を求めることができます。
 学生の方
学生の方やっぱり無限に描けないから、式をつくらないといけないよね?
一般のxについて、yの取りうる範囲がどのようになるかを式で表せばOKです。
xを定数とみなして、上記と同じように計算していきます。
右辺をaについて整理して、aの関数であると考えましょう。
\begin{array}{lll}
y&=&a^2+xa\\\\
&=&\left(a+\cfrac{1}{2}x\right)^2-\cfrac{1}{4}x^2
\end{array}aはすべての実数をとるので、yの最小値は-\cfrac{1}{4}x^2(最大値なし)
よって、yのとりうる範囲はy\geqq-\cfrac{1}{4}x^2
これがxとyの満たす条件であり、これを図示すると①の通過領域である(境界を含む)。

わかりやすさは「aの方程式」、汎用性は「1文字固定」
もちろん,どちらの方法でも同じ答えになりますが、aの方程式にする①の方法のほうが、わかりやすいという人が多いのではないかなと思います。
ただし、①の方法は、aの2次方程式になる場合でないと解くことができません。
一方、1文字を固定する②の方法は、最大値と最小値を求めることができればよいので、2次関数の形でなくても答えが出せます(数Ⅱの範囲内で解けない場合はあります)。
 粗茶さん
粗茶さん実際のところはaは2乗までしかないことが多いので、aの方程式にする方法で対応できることがほとんどです。
まとめ
この記事では「直線の通過領域」の問題について2通りの解き方と考え方を説明しました。
学校の授業ではあまり触れられることは多くない問題ですが、大学入試の二次試験ではよく出題されています。
もっと応用編でaの範囲がついている問題も出てきますが、まずは基本の考え方をしっかり身につけていきましょう!
このブログでは,自分で勉強しているとき,つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や,勉強が楽しくなる文房具も紹介していますので,よろしければご覧ください!



