【図形の性質】三角形の成立条件と式が成り立つ理由をわかりやすく解説！

学生の方

図形の問題で、三角形の成立条件ってのが出てきたんだけど、どういうこと？成立しないことがあるの？

最もよく出てくる図形といえば三角形ですが、

問題によっては三角形の成立条件を考える必要があることがあります。

こんな式です。

\large|a-b| < c < a+b

なんだかわかるようなわからないような式ですよね。

特に絶対値がついてるところとかが謎だと思います。

この記事では、三角形が成立する条件と、公式の成り立ちについて解説していきます。

この記事を書いた人

粗茶

• 文系に特化して数学を分かりやすく教える高校数学の専門家
• 指導歴15年
• 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

他の2辺の和より長い辺があると三角形は描けない

冒頭の公式はとりあえずおいといて、

三角形が成立する条件を言葉で表すと、

すべての辺が、他の2辺の和より短い

これです。

例えば、3辺の長さが1，2，50っていう三角形、描けますか？

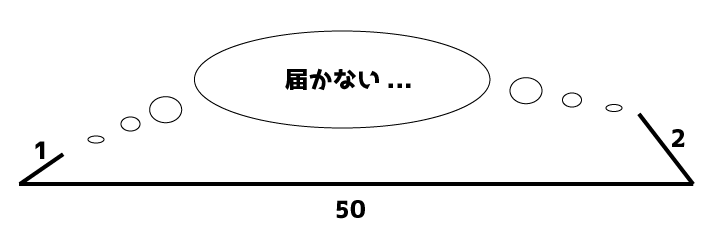
1と2の辺がお互い遠すぎて、絶対くっつかないですよね。

このように、2辺の長さを足してももう1辺の長さに達しない場合、三角形が成立しません。

三角形の成立条件を式で表す

三角形の各辺は、他の2辺の長さの和よりも小さい

ということを式に表せば、三角形の成立条件となります。

\left\{
\begin{array}{ll}
a < b+c\\\\
b < c+a\\\\
c < a+b　
\end{array}
\right.

この考え方でいくと、すべての辺の組み合わせを考えないといけないので、式が３つになってしまいます。

abc→bca→cabって風に対称性があっていいんですが、せっかくなら１つの式にまとめたいという欲求がでてきますよね。

学生の方

出ません！

粗茶さん

まあ、そこをなんとか…

3つの式を1つにまとめる

ここからは、三角形の成立条件の3つの式を1つにまとめていきます。

3つの式に番号をつけまして、

\left\{
\begin{array}{ll}
a < b+c　\cdots①\\\\
b < c+a　\cdots②\\\\
c < a+b　\cdots③
\end{array}
\right.

①と②を移項して、右辺をcにすると、

\left\{
\begin{array}{ll}
a-b < c　\cdots①\\\\
b-a < c　\cdots②\\\\
c < a+b　\cdots③
\end{array}
\right.

この段階で③の式は、目標とする式の右側の部分になっていますよね。

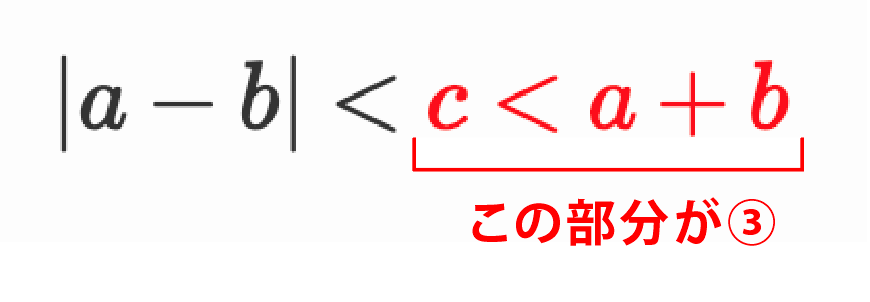
ということは、①と②を使って、左側の部分ができればいいわけです。

①かつ②、つまり、「a-b<c　かつ　b-a<c」を１つにまとめます。

学生の方

でも、aとbのどっちが大きいかがわからないなあ…

そうなんですよ。

a-b　と　b-a　の大小は、aとbの大小によって変わってきてしまいます。

どっちが大きいかわからないときは、そう、場合分けです。

まず、a>bのときは、b-a　よりも　a-b　のほうが大きいので、

「a-b<c　かつ　b-a<c」は、「a-b<c」となります。

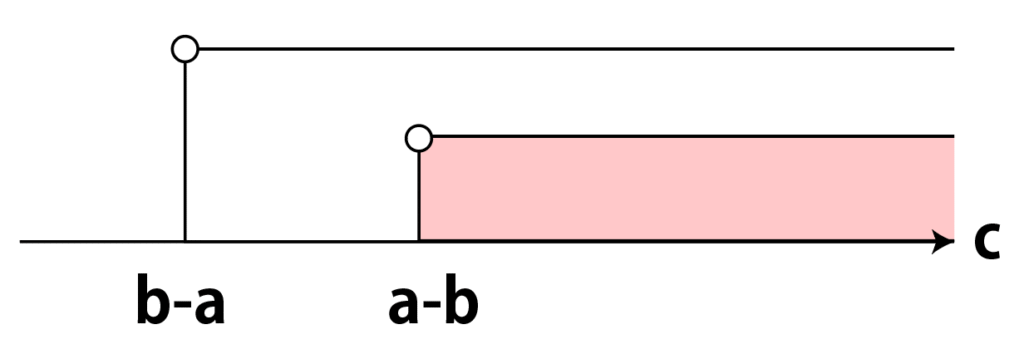
逆にb>aのときは、a-b　よりも　b-a　のほうが大きいので、

「a-b<c　かつ　b-a<c」は、「b-a<c」です。

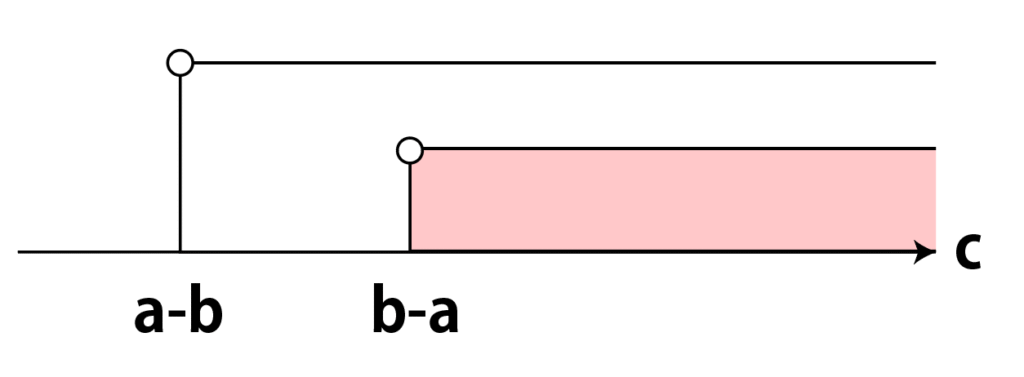
あと、a=bのときは、a-b　と　b-a　は同じなので、

「a-b<c」に含めておきますね。

（b-a<cに含めてもよい）

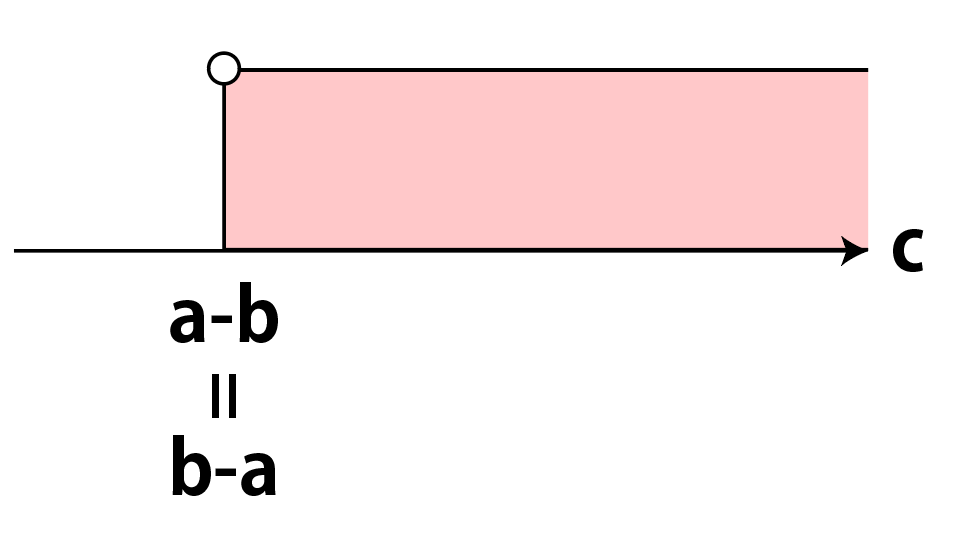
ここまでの話をまとめると、①かつ②とは、

\left\{
\begin{array}{lll}
a\geqq b&のとき，a-b < c \\\\
a < b&のとき，b-a< c
\end{array}
\right .

そしてこれがなんと、次のようにまとまります！

\color{red}\large |a-b| < c

学生の方

絶対値！？

突然の絶対値の登場に戸惑いを隠せないかもしれませんが、実際に絶対値を外してみると同じになることがわかります。

絶対値の外し方については次の記事も参照してください。

あわせて読みたい

絶対値の外し方，意外と簡単です。基本をしっかりマスターしよう！ 絶対値が出てくると，やる気なくすわー。 絶対値の外し方で悩んでいませんか？ 中学校では「符号を取り除く」だけで終わっていた絶対値。 高校では単純な計算問題だけで…

まず、絶対値の中身が0以上、つまりa-b\geqq 0のとき、a\geqq bであり、

絶対値はそのままはずせるので、

|a-b|=a-b

よって不等式は

a-b< c

になります。

逆に、絶対値の中身が負、

つまりa-b < 0のとき、a<bであり、

絶対値は-1倍してはずすので、

|a-b|=-(a-b)=b-a

よって不等式は

b-a< c

となります。

したがって、

\large |a-b| < c

と

\left\{
\begin{array}{lll}
a\geqq b&のとき，a-b < c \\\\
a < b&のとき，b-a< c
\end{array}
\right .

は同じということがわかりましたね。

以上のことを踏まえると

\left\{
\begin{array}{ll}
a < b+c　\cdots①\\\\
b < c+a　\cdots②\\\\
c < a+b　\cdots③
\end{array}
\right.

は、①かつ②より、

|a-b|< c

そして③より

c< a+b

が成り立つことがわかったので、これらの共通範囲を考えると、

\large\color{Red}|a-b|< c < a+b

が完成しました！

ということで、三角形の成立条件は、

1つの辺が、他の2辺の和より小さく、かつ他の2辺の差の絶対値よりも大きい

と考えることもできるのです。

まとめ

この記事では、三角形の成立条件の式と、成り立つ理由について解説しました。

共通テストなどの問題で、辺の長さを計算した結果、2つの値が出てきたのに、解答欄が1つしかない！といった状況はよくあります。

そんなときに三角形の成立条件に当てはまるかどうかを考えることで、答えを１つに絞ることができる可能性があります。

意外な盲点になりそうなトピックなので、図形を扱う問題では気をつけておきたいですね。

　

このブログでは，自分で勉強しているとき，つまづきやすいポイントを解説。

「かゆいところに手が届く」情報を発信しています。

自分で勉強する際にオススメの参考書や，勉強が楽しくなる文房具も紹介していますので，よろしければご覧ください！

あわせて読みたい

製図用シャープで楽しく勉強！ノートがパッと華やぐ！ ノートが汚くて自分でも読めないときがあるんだよね。 「製図用シャープ」があなたのノートのお悩みを解決します。 製図用シャープは、ただの筆記具ではありません。 あ…

あわせて読みたい

【高校生】数学が全くわからないあなたへ！自分で勉強できるおすすめ参考書ガイド 数学の先生が変わって， 先生が何言ってるか全然わからない。ピンチ… という状況で悩んでいませんか？ 私も高校生の時，そうでした。 高１のときの先生はよかったけど，…