三角形の面積の公式といえば，何を知っていますか？
学生の方底辺×高さ÷２
一般的に知られているのは「底辺✕高さ÷２」だと思います。
もちろんこれは重要な公式で，高校数学でも使う機会は多くあります。
しかし，高校に入ると，複数の単元で三角形の面積公式を学習することになります。
この記事では，高校までの範囲で学習する三角形の面積公式を５つまとめて紹介します。
粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴14年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。
三角形の面積①：底辺✕高さ÷2
三角形の面積といえば，小学校で習う「底辺✕高さ÷２」がありますね。
中学校までの間は，基本的にこの公式１本で戦うことになります。
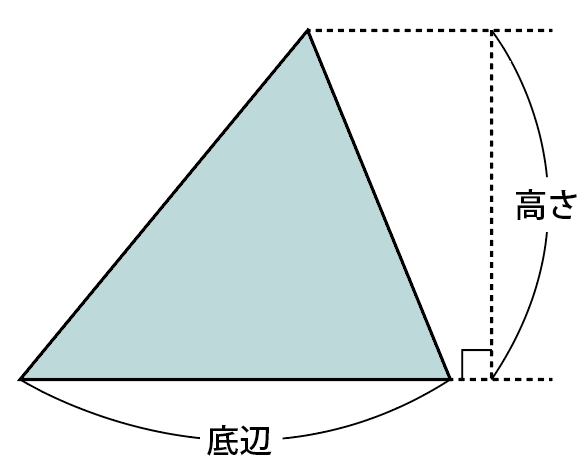
図で，三角形の面積は，
底辺×高さ÷2
なぜ「底辺×高さ÷２」で三角形の面積が出るのかを説明しておきます。
直角三角形になるように，上の頂点を真横にスライドさせます。
動かしても，底辺と高さは変わりません。
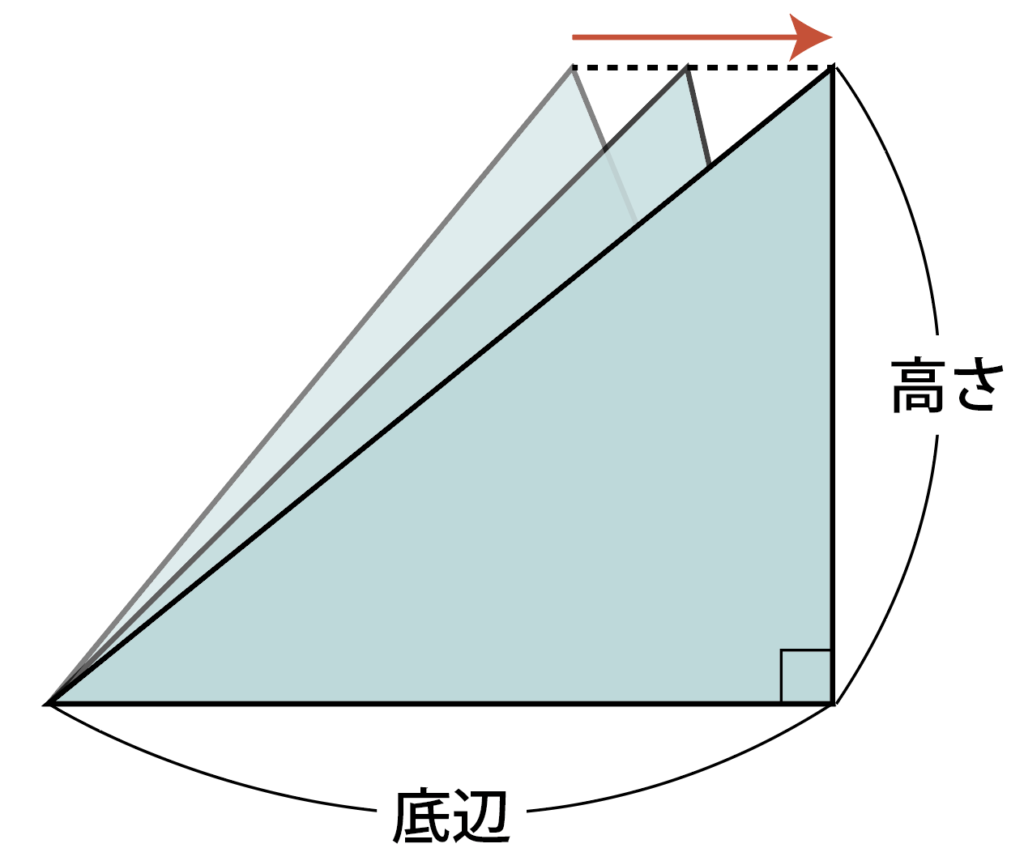
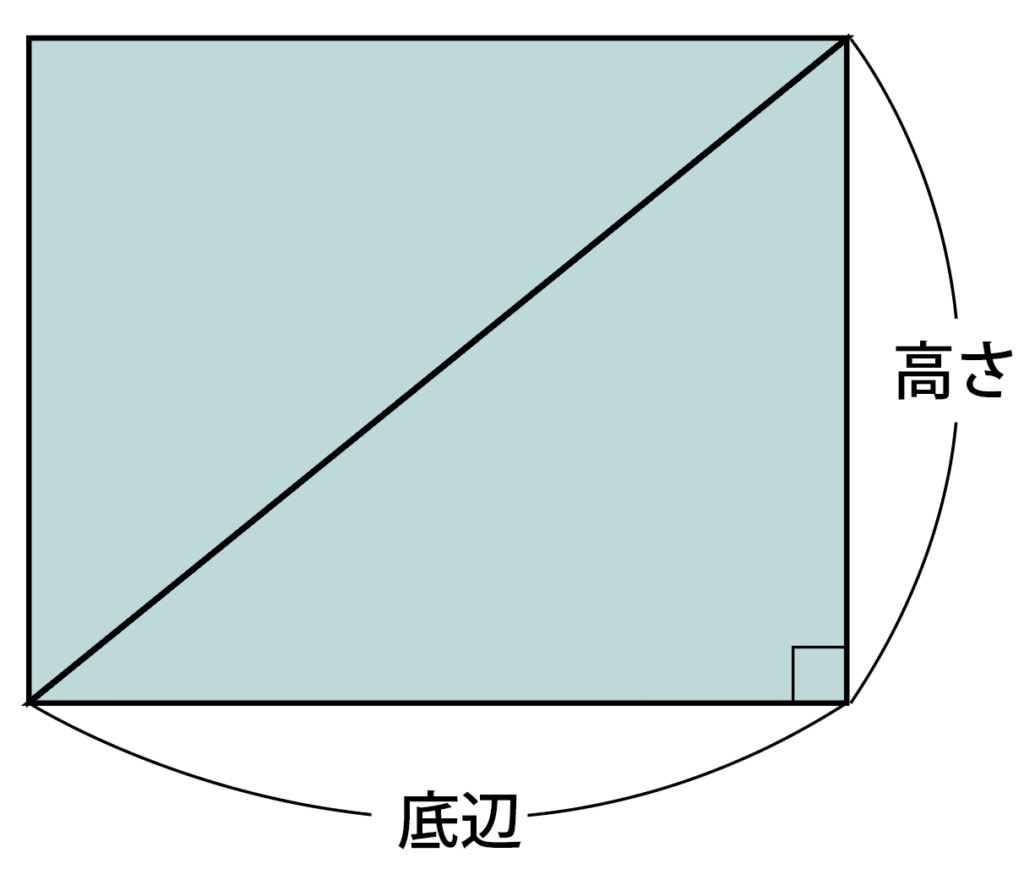
できあがった直角三角形と同じものをひっくりかえしてくっつけると，長方形になります。
この長方形の面積は「たて×よこ」なので，図でいうと
「底辺✕高さ」ということ。
三角形の面積は長方形の半分なので，
「底辺×高さ÷２」
になります。
三角形の面積②：２辺と間の角のsin
高校数学で「三角比（サイン・コサイン・タンジェント）」を習うと，底辺と高さがわかっていない三角形でも面積を求められるようになります。
おそらく最初に習うのが「２辺と間の角のsin」から面積を求める方法。
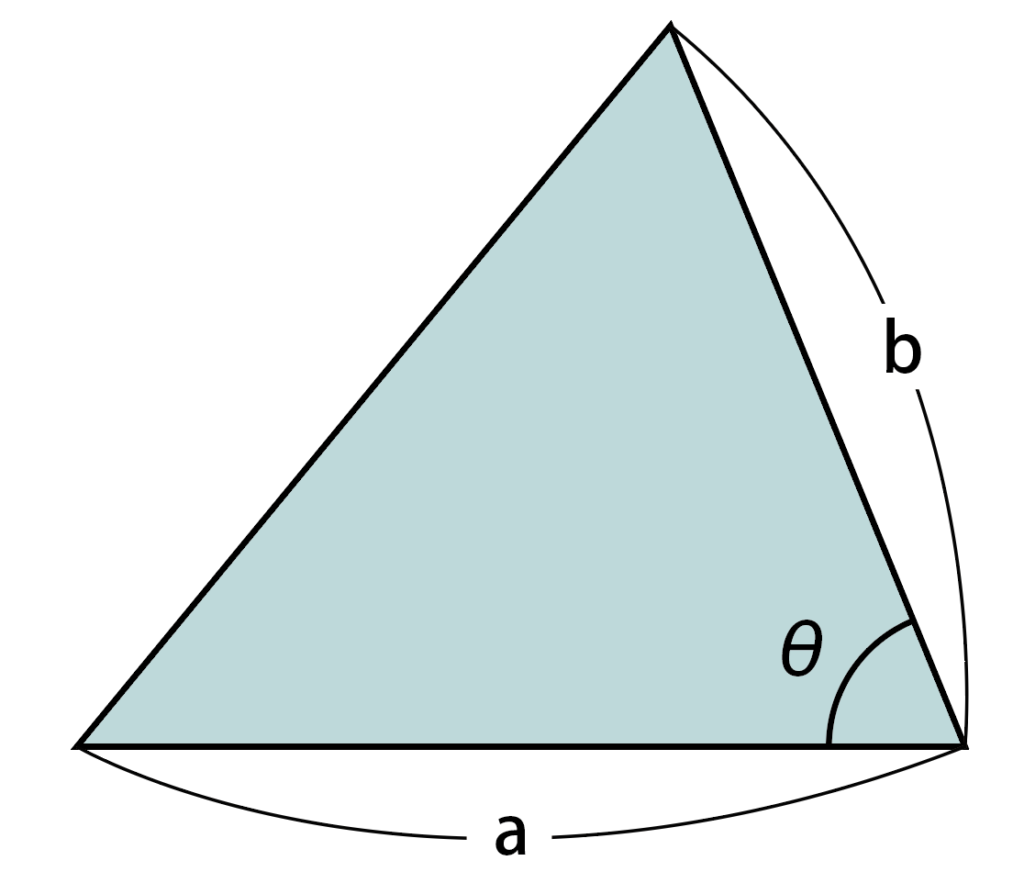
図で，三角形の面積は，
\cfrac{1}{2}ab\sin\theta
底辺をaとしたときの高さを表すことで，公式を導きます。
図のように，頂点から底辺にむかって垂線をひきます。
左の直角三角形に注目すると，三角比の定義より，
\sin\theta=\cfrac{h}{b}よって，
h=b\sin\theta
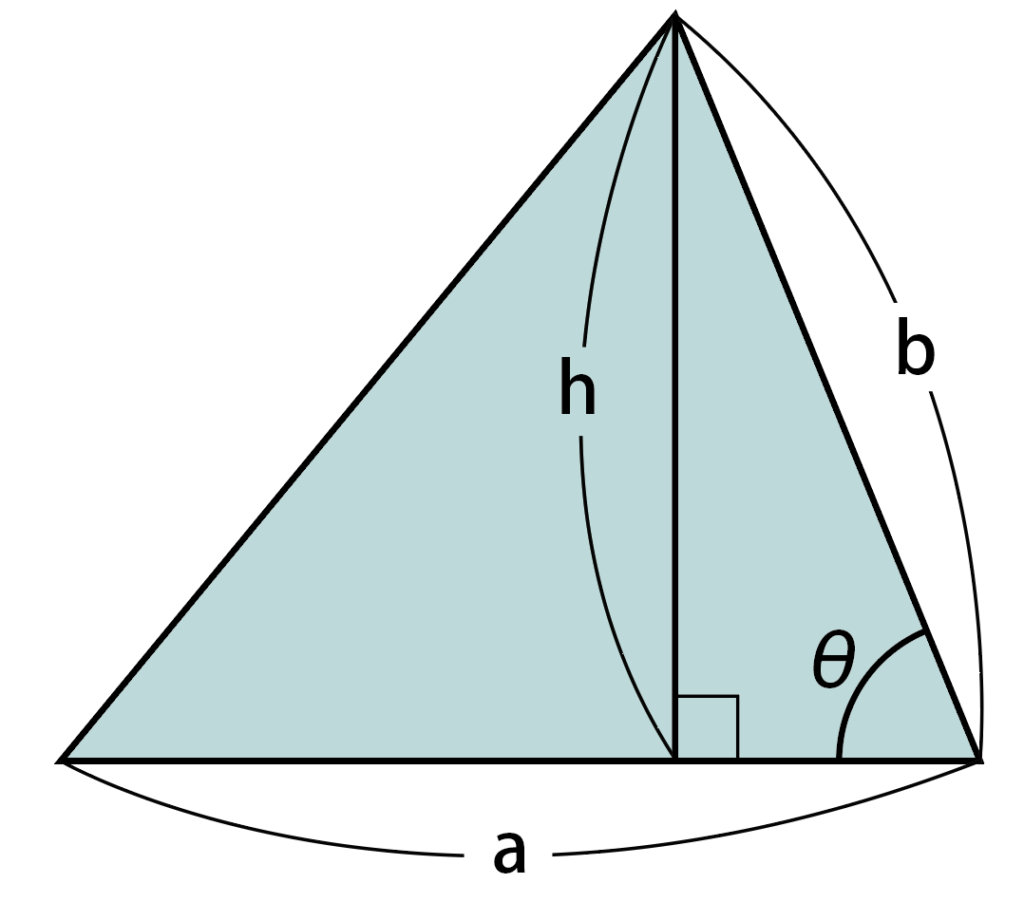
底辺がa，高さがb\sin\thetaなので，
「底辺✕高さ÷２」にあてはめて，面積は，
a\times b\sin\theta\div 2＝\cfrac{1}{2}ab\sin\theta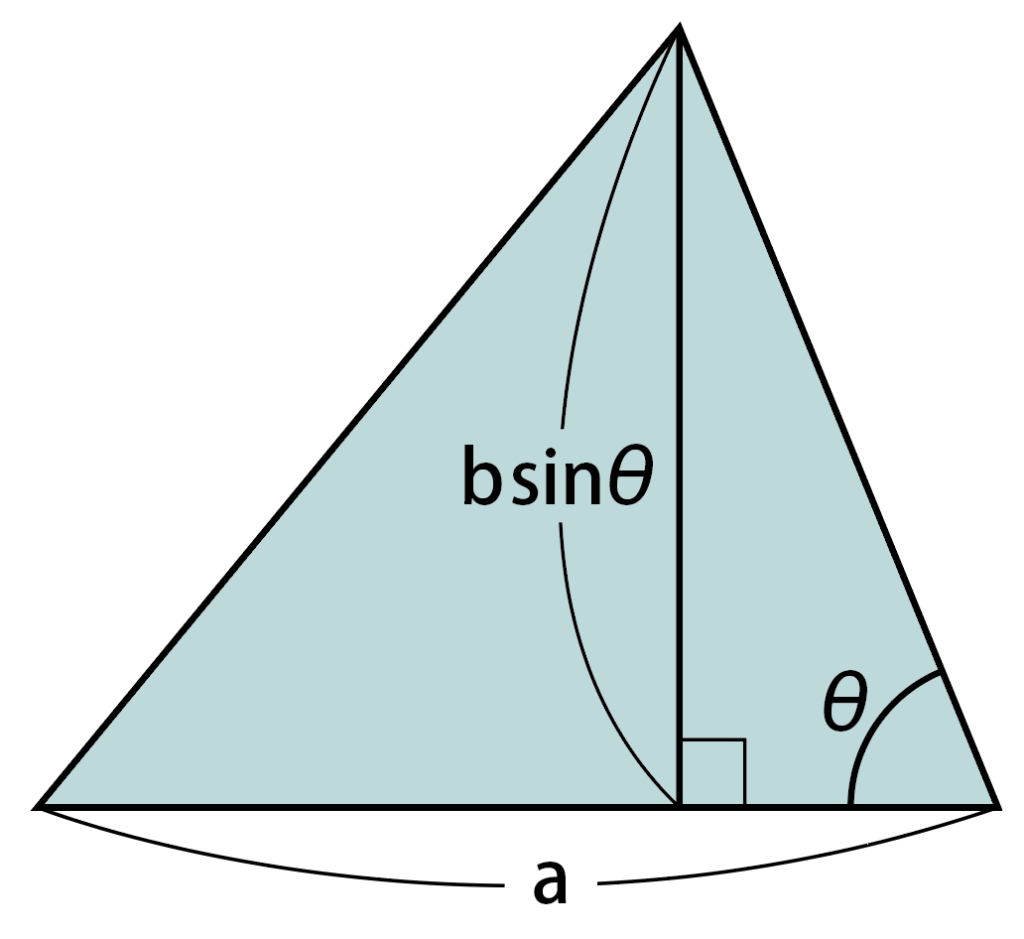
三角形の面積③：ヘロンの公式
３つの辺の長さがわかっているときは，三角比を知らなくても面積を求められる夢のような公式があります。
その名も「ヘロンの公式」
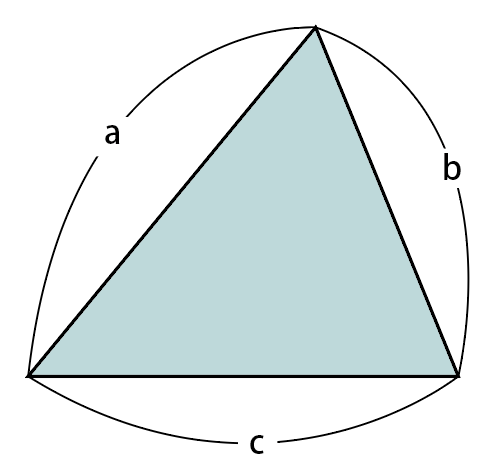
図の三角形について，
s=\cfrac{a+b+c}{2}とすると，
面積は，
\sqrt{s(s-a)(s-b)(s-c)}
学生の方…なんかめんどくさそう。
そうなんです。ヘロンの公式は，辺の長さだけで面積を求められる反面，式が複雑になりがちです。
具体例でやってみましょう。
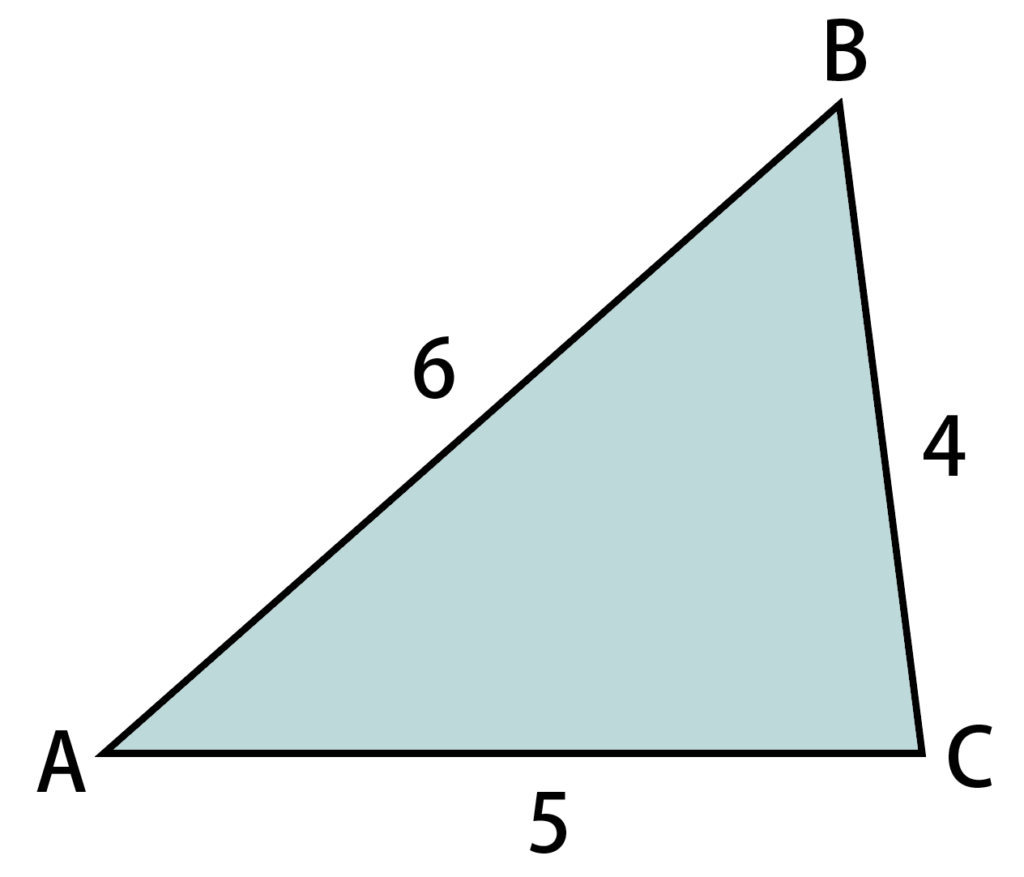
図の三角形ABCの面積を求めなさい。
a=4，b=5，c=6としておきます。
s=\cfrac{4+5+6}{2}=\cfrac{15}{2}なので，ヘロンの公式にあてはめて，面積は，
\begin{aligned}&\sqrt{\cfrac{15}{2}\left(\cfrac{15}{2}-4\right)\left(\cfrac{15}{2}-5\right)\left(\cfrac{15}{2}-6\right)}\\\\
＝&\sqrt{\cfrac{15}{2}\cdot\cfrac{7}{2}\cdot\cfrac{5}{2}\cdot\cfrac{3}{2}}\\\\
＝&\cfrac{15\sqrt{7}}{4}\end{aligned}ってすれば出せるんですが，ヘロンの公式を覚えている人は少ない（筆者も覚えていない）ので，現実的には，余弦定理でcosを求めてから，sinを用いた公式で面積を求める流れにすることが多いです。
（現実的なやり方）
余弦定理で，
\cos{\rm A}＝\cfrac{6^2+5^2-4^2}{2\cdot 6\cdot 5}＝\cfrac{45}{60}
＝\cfrac{3}{4}0^{\circ}<{\rm A}<180^{\circ}だから，
\sin{\rm A}＝\sqrt{1-\left(\cfrac{3}{4}\right)^2}＝\cfrac{\sqrt{7}}{4}求める三角形の面積は，
\cfrac{1}{2}bc\sin{\rm A}＝\cfrac{1}{2}\cdot 5\cdot 6\cdot \cfrac{\sqrt{7}}{4}＝\cfrac{15\sqrt{7}}{4}式の長さとしては，ヘロンの公式のほうが短いですが，実際の入試問題では，面積の前に余弦定理でcosを求めさせたりする誘導があるので，誘導に従って解いたほうが，無駄な計算がなくてすみます。
状況に応じて使い分けることが大切です。
ヘロンの公式は，先程の「2辺と間の角のsin」の公式から導けますが，長くなるので，気になる人だけクリックして見てください。
ヘロンの公式の証明
\begin{aligned}
&\cfrac{1}{2}ab\sin C\\\\
=&\cfrac{1}{2}ab\sqrt{1-\cos^2C}\\\\
=&\cfrac{1}{2}ab\sqrt{1-\left(\cfrac{a^2+b^2-c^2}{2ab}\right)^2}\\\\
=&\cfrac{1}{2}ab\sqrt{\cfrac{4a^2b^2-(a^2+b^2-c^2)^2}{4a^2b^2}}\\\\
=&\cfrac{1}{2}ab\cfrac{\sqrt{4a^2b^2-(a^2+b^2-c^2)^2}}{2ab}\\\\
=&\cfrac{1}{4}\sqrt{(2ab)^2-(a^2+b^2-c^2)^2}\\\\
=&\cfrac{1}{4}\sqrt{{2ab+(a^2+b^2-c^2)}{2ab-(a^2+b^2-c^2)}}\\\\
=&\cfrac{1}{4}\sqrt{{(a^2+2ab+b^2)-c^2}{c^2-(a^2-2ab+b^2)}}\\\\
=&\cfrac{1}{4}\sqrt{{(a+b)^2-c^2}{c^2-(a-b)^2}}\\\\
=&\cfrac{1}{4}\sqrt{(a+b+c)(a+b-c)(c+a-b)(c-a+b)}\\\\
=&\sqrt{\cfrac{a+b+c}{2}\cdot\cfrac{a+b-c}{2}\cdot\cfrac{c+a-b}{2}\cdot\cfrac{c-a+b}{2}}\\\\
=&\sqrt{\cfrac{a+b+c}{2}\cdot\cfrac{a+b+c-2c}{2}\cdot\cfrac{a+b+c-2b}{2}\cdot\cfrac{a+b+c-2a}{2}}\\\\
=&\sqrt{\cfrac{a+b+c}{2}\left(\cfrac{a+b+c}{2}-c\right)\left(\cfrac{a+b+c}{2}-b\right)\left(\cfrac{a+b+c}{2}-a\right)}\\\\
\end{aligned}ここで，\cfrac{a+b+c}{2}=sとすれば，
\begin{aligned}
\sqrt{s(s-c)(s-b)(s-a)}
\end{aligned}三角形の面積④：ベクトルの大きさと内積
ベクトルを用いた三角形の面積公式は２種類あります。
まずは大きさと内積を用いたもの。
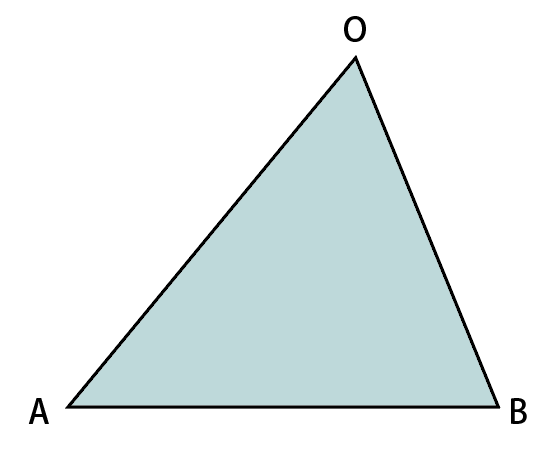
図の三角形の面積は，
\cfrac{1}{2}\sqrt{|\overrightarrow{\rm OA}|^2|\overrightarrow{\rm OB}|^2-(\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB})^2}
この公式は，②の\cfrac{1}{2}ab\sin\theta をもとにつくられています。
\angle{\rm AOB}=\thetaとすると，面積は，
\cfrac{1}{2}|\overrightarrow{\rm OA}||\overrightarrow{\rm OB}|\sin\theta＝\cfrac{1}{2}\sqrt{|\overrightarrow{\rm OA}|^2|\overrightarrow{\rm OB}|^2\sin^2\theta}
粗茶さん\sin^2\theta+\cos^2\theta=1\\⇔\sin^2\theta=1-\cos^2\theta
を代入します
\begin{aligned}
&=\cfrac{1}{2}\sqrt{|\overrightarrow{\rm OA}|^2|\overrightarrow{\rm OB}|^2\left(1-\cos^2\theta\right)}\\\\&＝\cfrac{1}{2}\sqrt{|\overrightarrow{\rm OA}|^2|\overrightarrow{\rm OB}|^2-|\overrightarrow{\rm OA}|^2|\overrightarrow{\rm OB}|^2\cos^2\theta}\\\\&＝\cfrac{1}{2}\sqrt{|\overrightarrow{\rm OA}|^2|\overrightarrow{\rm OB}|^2-\left(|\overrightarrow{\rm OA}||\overrightarrow{\rm OB}|\cos\theta\right)^2}
\end{aligned}粗茶さん内積の定義で，
|\overrightarrow{\rm OA}||\overrightarrow{\rm OB}|\cos\theta\\=\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB}
なので，これを代入すると，できあがり。
\begin{aligned}
&＝\cfrac{1}{2}\sqrt{|\overrightarrow{\rm OA}|^2|\overrightarrow{\rm OB}|^2-(\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB})^2}
\end{aligned}すこし複雑さがありますが，ベクトルの単元ではよく使われるので，必ず覚えましょう。
三角形の面積⑤：ベクトルの成分
ベクトルの成分が与えられているときに，三角形の面積を求める公式もあります。
図の三角形について，
\overrightarrow{\rm OA}=(x_1,y_1),\overrightarrow{\rm OB}=(x_2,y_2)とすると，
面積は，
\cfrac{1}{2}|x_1y_2-x_2y_1|
どうしてこうなるのか，パッと見わからない感じですが，さきほどの「大きさと内積の公式」から導くことができます。
|\overrightarrow{\rm OA}|=\sqrt{{x_1}^2+{y_1}^2}，
|\overrightarrow{\rm OB}|=\sqrt{{x_2}^2+{y_2}^2}，
\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB}=x_1x_2+y_1y_2
なので，これらを代入していきます。
\begin{aligned}
&\cfrac{1}{2}\sqrt{|\overrightarrow{\rm OA}|^2|\overrightarrow{\rm OB}|^2-(\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB})^2}\\\\
=&\cfrac{1}{2}\sqrt{({x_1}^2+{y_1}^2)({x_2}^2+{y_2}^2)-(x_1x_2+y_1y_2)^2}\\\\
=&\cfrac{1}{2}\sqrt{{x_1}^2{x_2}^2+{x_1}^2{y_2}^2+{y_1}^2{x_2}^2+{y_1}^2{y_2}^2-({x_1}^2{x_2}^2+2x_1x_2y_1y_2+{y_1}^2{y_2}^2)}\\\\
=&\cfrac{1}{2}\sqrt{{x_1}^2{y_2}^2-2x_1y_2x_2y_1+{x_2}^2{y_1}^2}\\\\
=&\cfrac{1}{2}\sqrt{(x_1y_2-x_2y_1)^2}\\\\
=&\cfrac{1}{2}|x_1y_2-x_2y_1|\end{aligned}粗茶さんルートの中に２乗があるので，ルートは外れますが，
\sqrt{A^2}=|A|であることに注意。
かなりシンプルな式になりました。
絶対値がつく理由もわかっていただけたかと思います。
この公式は，３頂点の座標がわかっているときに力を発揮します。
xy平面上に3点\rm A(1，1)，B(-1，4)，C(4，3)がある。三角形ABCの面積を求めよ。
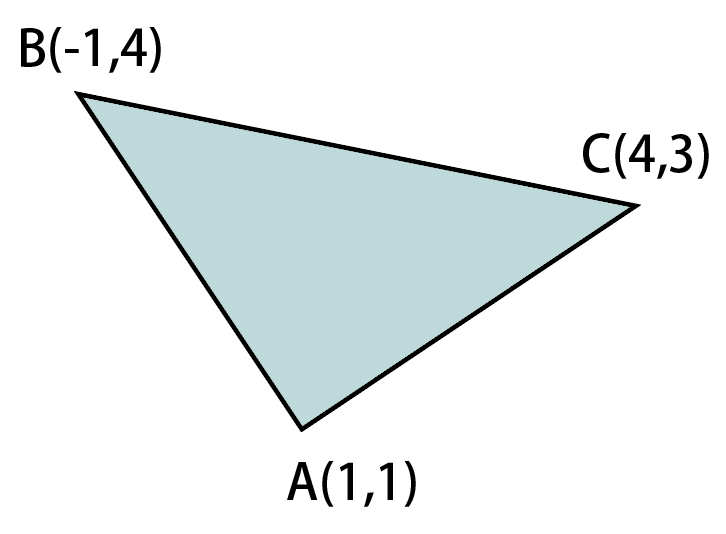
図示するとだいたいこんな感じ。
座標からベクトルを求めて，面積を計算します。
なので，面積は，
\cfrac{1}{2}|-2\cdot 2-3\cdot 3|=\cfrac{13}{2}座標を扱う問題ではよく使われるので，大きさと内積の公式とともに覚えておきましょう。
状況に応じて，適切な公式を使おう
というわけで，三角形の面積公式を５つ紹介しました。
もう一度まとめると，次のものがありました。
- 底辺✕高さ÷２
- 2辺と間の角のsinをかけて，2で割る
- 3辺がわかっているときは，ヘロンの公式
- ベクトルの大きさと内積の公式
- ベクトルの成分から求める公式
与えられた条件に応じて，適切な公式を使えるように，経験を積むことが大切ですね。
このブログでは，自分で勉強しているとき，つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や，勉強が楽しくなる文房具も紹介していますので，よろしければご覧ください！
