位置ベクトルを学習する上で、絶対に外せない公式というか事実があります。
点Pが直線AB上にあるとき、
\overrightarrow{\rm OP}=s \overrightarrow{\rm OA}+t \overrightarrow{\rm OB}(s+t=1)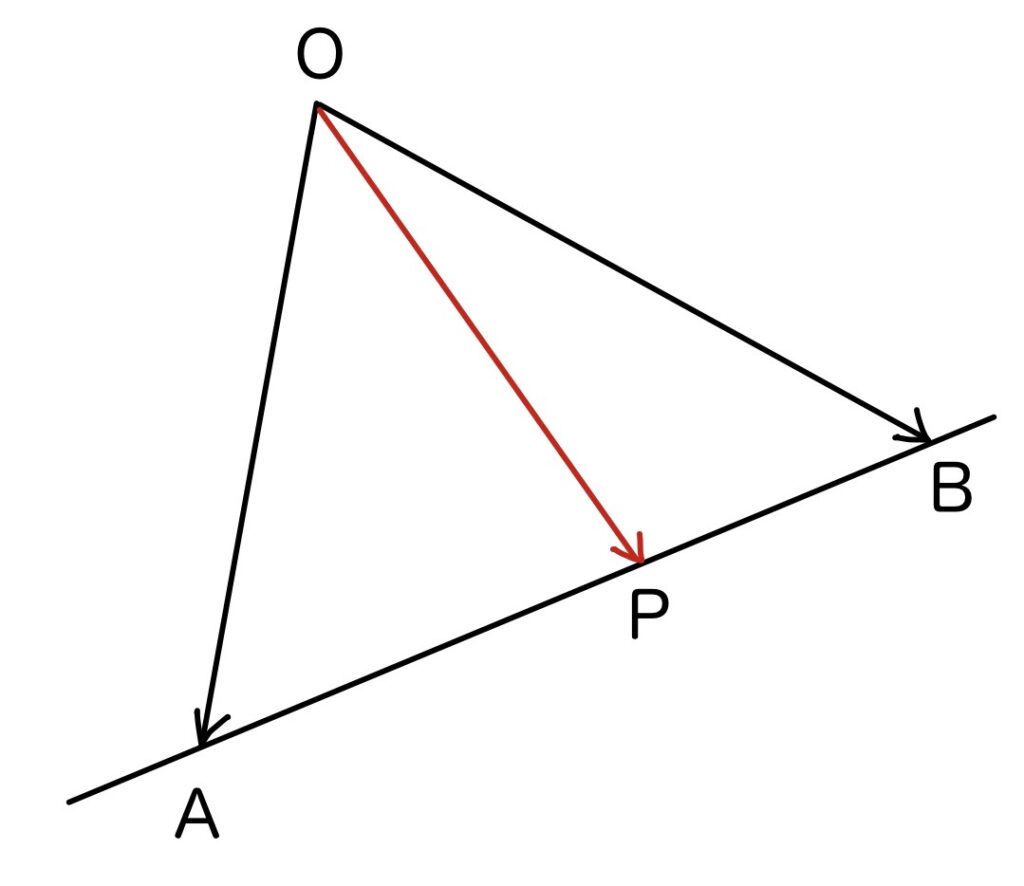
この\overrightarrow{\rm OA}と\overrightarrow{\rm OB}の係数の和が1になるところが重要なんですが、
 学生の方
学生の方何でs+tが1になるの?
って疑問に思ったことがあるんじゃないでしょうか?
この記事では、ベクトルを使った直線上の点の表し方をわかりやすく解説します。
あわせて、空間における平面上の点の表し方も紹介します。
理由がわかった上で使えると、公式の暗記の助けになると思いますよ。

粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

平面における直線上の点の表しかた
それでは、直線上の点の表し方について、順を追って解説していきます。
平行ならば実数倍
直線AB上に点Pがあるとき、A,B,Pは同一直線上にあります。
すると、\overrightarrow{\rm AP}と\overrightarrow{\rm AB}は平行ということになります。
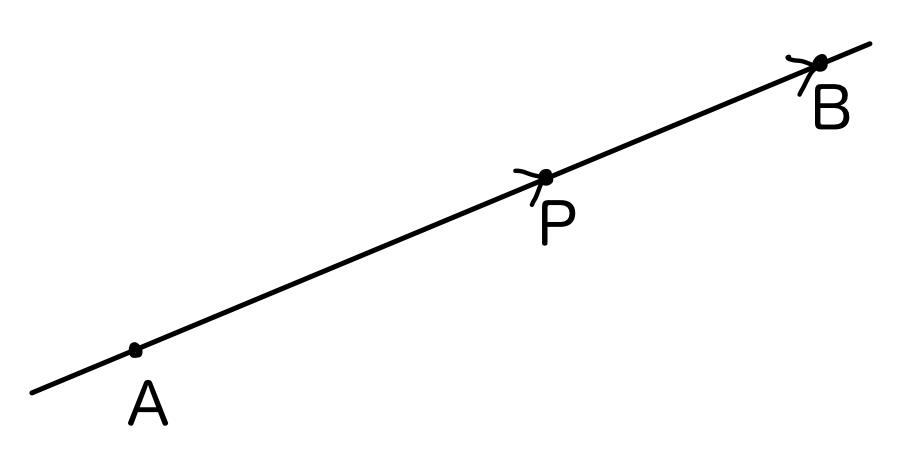
ということは、\overrightarrow{\rm AB}を何倍かすれば\overrightarrow{\rm AP}になるってこと。
つまり、kを実数とすると、
\large \overrightarrow{\rm AP}=k\overrightarrow{\rm AB}って書けます。
 粗茶さん
粗茶さんこの表し方もとても重要です。
始点をOにする
ベクトルの計算においては、始点を変えることがとても重要です。
先ほどの式は始点がAのベクトルで書かれていますが、これを原点Oが始点になるように変換します。
ベクトルの引き算(後ろー前)を使うことで、始点を好きな点に変えられましたよね。
\overrightarrow{\rm AB}=\overrightarrow{\rm ⬜︎B}-\overrightarrow{\rm ⬜︎A}(⬜︎には同じ点が入る)
今回の式を、始点をOに変換して、整理していきましょう。
\begin{array}{lrll}
&\overrightarrow{\rm AP}&=&k\overrightarrow{\rm AB}\\\\
\Leftrightarrow&\overrightarrow{\rm OP}-\overrightarrow{\rm OA}&=&k(\overrightarrow{\rm OB}-\overrightarrow{\rm OA})\\\\
\Leftrightarrow&\overrightarrow{\rm OP}&=&{\color{red}(1-k)}\overrightarrow{\rm OA}+{\color{red}k}\overrightarrow{\rm AB}
\end{array}ここで\overrightarrow{\rm OA}と\overrightarrow{\rm OB}の係数に注目すると、
\overrightarrow{\rm OA}の係数が\color{red}1-k、\overrightarrow{\rm OB}の係数が\color{red}kで、これらの和が1になっていますよね。
この「係数の和が1」ということがとても重要です。
 粗茶さん
粗茶さんこの形だと文字が1種類ですむので、よく使われます。
sとtに置き換えることで完成
さらに、1-kをsに、kをtに置き換えれば、最初の式になるというわけです。
1-kとkをたすと1になるわけなので、sとtを足しても1になりますよね。
\begin{array}{c}
\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}\\\\(ただし,s+t=1)
\end{array}これで完成。
s+t=1になる仕組みもわかってもらえたかと思います。
空間における平面上の点の表し方
同じような考え方で、空間図形における平面上の点も表すことができます。
3点A,B,Cを含む平面上に点Pがあるとき、
\begin{array}{c}
\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}+u\overrightarrow{\rm OC}\\\\
(s+t+u=1)
\end{array}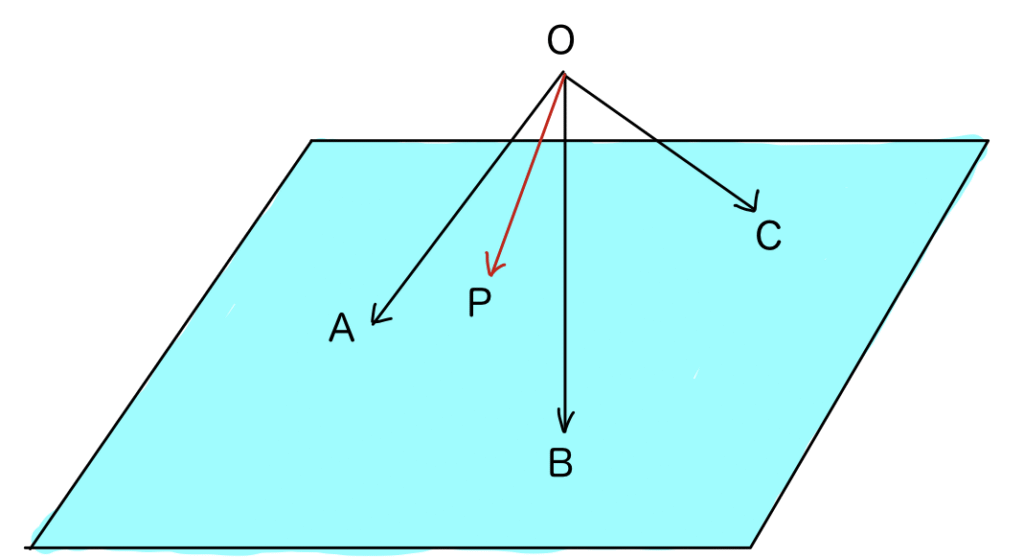
同一平面上の点は、異なる2つのベクトルで表せる
まず、点Pは点A,B,Cと同一平面上なので、\overrightarrow{\rm AP}は\overrightarrow{\rm AB}と\overrightarrow{\rm AC}で表すことができます。
\overrightarrow{\rm AP}=x\overrightarrow{\rm AB}+y\overrightarrow{\rm AC}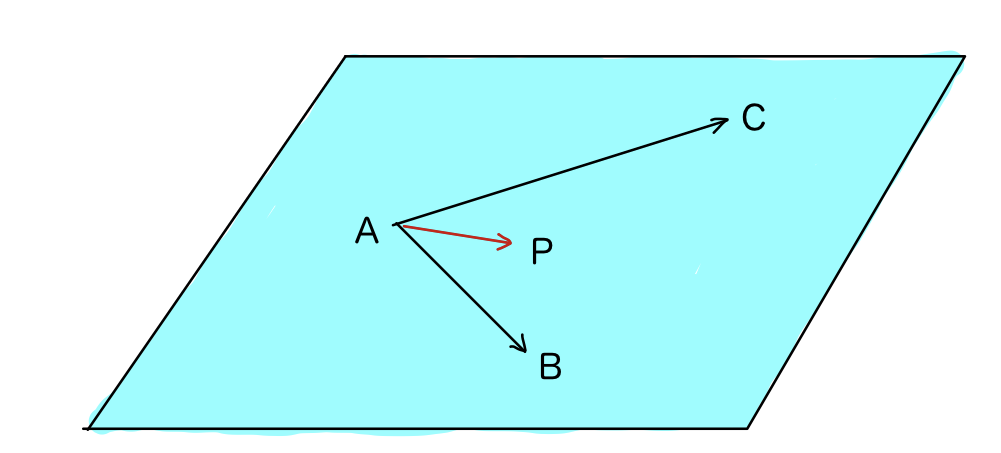
このとき、xとyの値に制限はありません(xとyの和は1でなくてもよい)。
始点をOに揃える
そして、それぞれのベクトルの始点をOに変換します。
\begin{array}{rrll}
&\overrightarrow{\rm AP}&=&x\overrightarrow{\rm AB}+y\overrightarrow{\rm AC}\\\\
\Leftrightarrow&\overrightarrow{\rm OP}-\overrightarrow{\rm OA}&=&x(\overrightarrow{\rm OB}-\overrightarrow{\rm OA})+y(\overrightarrow{\rm OC}-\overrightarrow{\rm OA})\\\\
\Leftrightarrow&\overrightarrow{\rm OP}&=&{\color{red}(1-x-y)}\overrightarrow{\rm OA}+{\color{red}x}\overrightarrow{\rm OB}+{\color{red}y}\overrightarrow{\rm OC}
\end{array}ここで\overrightarrow{\rm OA},\overrightarrow{\rm OB},\overrightarrow{\rm OC}の係数に注目すると、
\overrightarrow{\rm OA}の係数\color{red}1-x-y,\overrightarrow{\rm OB}の係数\color{red}x,\overrightarrow{\rm OC}の係数\color{red}yの和が1になっていますよね。
さっきの直線上のベクトルと同じ流れになってきました。
s,t,rに置き換えて完成
1-x-yをs,xをt,yをuとすると,最初の式になります。
1-x-yとxとyをたすと1になるわけなので、sとtとuを足しても1になります。
\begin{array}{c}
\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}+u\overrightarrow{\rm OC}\\\\
(ただし,s+t+u=1)
\end{array}平面における直線上の点の場合と同じ形をしているので、あわせて覚えておくといいですね!
まとめ
この記事では、ベクトルで出てくる直線上の点と平面上の点の表し方と、式の成り立ちについて解説しました。
位置ベクトルの問題を解く上で「係数の和が1」という事実は頻繁に使うことになるので、しっかり覚えておきましょう!
このブログでは,自分で勉強しているとき,つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や,勉強が楽しくなる文房具も紹介していますので,よろしければご覧ください!