 学生の方
学生の方PとCってあるじゃん?いつもどっちを使えばいいかわかんなくなるんだよね…
数Aの「場合の数」で登場する_nP_r(順列)と_nC_r(組合せ),
問題によって使い分けができなくて悩んでいませんか?
実はPとCの違いは非常にシンプルです。
- _nP_r…異なるn個のものからr個を取り出して,1列に並べる並べ方の総数
- _nC_r…異なるn個のものからr個を取り出す,取り出し方の総数(順番は考えない)
実は,異なるn個のものからr個を取り出すところまでは同じで,
そのあと並べるか並べないかの違いでしかありません。
この記事では,「場合の数」を学習する上で基本となる_nP_r(順列)と_nC_r(組合せ)の違いと計算方法をわかりやすく解説していきます。
- 場合の数で使う_nP_r(順列)と_nC_r(組合せ)の違いと計算方法がわかる

粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

階乗は,自然数を全部かけたもの
順列と組み合わせを語る前に,重要な計算である階乗について紹介します。
自然数を1からnまで全部かけあわせたものをnの階乗といい,
n!
と書きます。
「1からnまで」と書きましたが,ふつうは大きい方から順にかけるので,
例えば,「5の階乗」は,
5!=5\cdot4\cdot3\cdot2\cdot1=120
となります。
階乗の値はある程度覚えていると便利なので,一覧にしておきます。
\begin{array}{l}
0!=1\\\\
1!=1\\\\
2!=2\cdot 1=2\\\\
3!=3\cdot2\cdot 1=6\\\\
4!=4\cdot3\cdot2\cdot 1=24\\\\
5!=5\cdot4\cdot3\cdot2\cdot 1=120\\\\
6!=6\cdot5\cdot4\cdot3\cdot2\cdot 1=720\\\\
\end{array}7!より先はあまり使わないので,その都度計算すればいいと思います。
 粗茶さん
粗茶さん6!までの値も,その都度計算すればいいっちゃ,いい。
 学生の方
学生の方0の階乗はどうして1なの?
さりげなく書いてしまいましたが,0の階乗は1であると定義されています。
理由は,そうしておくと何かと都合がいいから,です。
 粗茶さん
粗茶さん定義なので,ここは我慢して覚えましょう…
P(順列)は,取り出したものを並べる
それではここからは,_nP_r(順列)について説明していきます。
Pの定義
_nP_r(順列)の定義は次のようになります。
異なるn個のものからr個を選んで,一列に並べる並べ方(順列という)の総数を_nP_rと表し,次のように計算する。

文字で書かれると分かりづらいと思うので,具体的な問題をやってみましょう。
上のように,A,B,C,D,Eの文字が書かれたカードが1枚ずつある。
この5枚の中から3枚を選んで1列に並べる並べ方の総数を求めなさい。
異なる5個から3個を選んで,並べるので,
_5P_3になります。
5から始めて3回かければいいので,
_5P_3=5\cdot 4\cdot 3=60
よって60通り。
という感じで,取り出して「並べる」工程が入っている場合はPを使います。
Pの意味
 学生の方
学生の方どうしてこの計算になるの?
それでは,先程の例題1をPを使わずに考えてみましょう。
5枚のカードから1枚ずつ選んで,左から順に並べていきます。
まず,左端のカードを選びます。選び方は5通り。
それぞれに対して,真ん中のカードの選び方が4通り(すでに1枚選ばれているため)。
それぞれに対して,右端のカードの選び方が3通り(すでに2枚選ばれているため)。
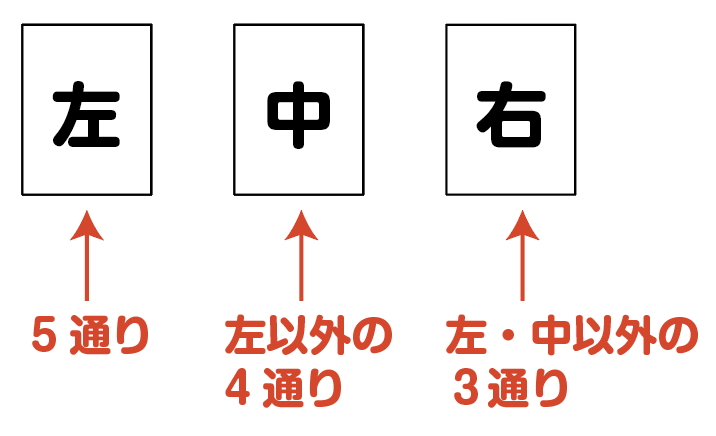
よって,並べ方の総数は
5\cdot 4\cdot 3=60
つまり60通り。
たしかに,_5P_3と同じ計算になりましたね。
このように順列の総数は,かんたんな掛け算で計算できるので,
無理してPで表現しなくても,掛け算でやってしまえばいい。
と,個人的には思っています。
 粗茶さん
粗茶さんただ,問題集の解説にPが使われていることが多いので,意味はわかっておこう。
全部並べるときは階乗を使う
順列の問題ですが,先ほどと少しだけ違います。

A,B,C,D,Eの文字が書かれたカードが1枚ずつある。
この5枚のカードを1列に並べる並べ方の総数を求めなさい。
例題1と違って,「3枚取り出す」という手順がなくなりました。
つまり,5枚を全部並べることになります。
5枚全部を並べる場合でも,「異なる5枚の中から5枚を選んで並べる」と考えれば,Pを使うことができます。
求める並べ方は,
_5P_5=5\cdot 4\cdot 3\cdot 2\cdot 1=120
よって120通り。
これ,どこかで見たことありますよね?
そう,5の階乗と同じなんです。
 粗茶さん
粗茶さん5から始めて5個かけるということは,5から1までかけるってことだからね。
Pの前後の数字が同じ場合は,階乗の計算になります。
_nP_n=n!
一部を取り出さずに,全部並べるときは,Pの形を書かずに,最初から階乗でいきましょう。
C(組合せ)は,取り出すだけ
続きまして,_nC_r(組合せ)について説明していきます。
まずは定義から。
Cの定義
_nC_r(組合せ)の定義は次のようになります。
異なるn個のものからr個を選ぶ選び方の総数を_nC_rと表し,次のように計算する。

_nP_rをr!で割ると,_nC_rになる。という関係があります。

A,B,C,D,Eの文字が書かれたカードが1枚ずつある。
この5枚の中から3枚を選ぶ,選び方の総数を求めなさい。
5枚から3枚を選びますが,並べることはしません。
選ぶだけで並べない場合は,Cを使いましょう。
異なる5個から3個を選ぶので,_5C_3です。
求める選び方の総数は,
_5C_3=\cfrac{5\cdot 4\cdot 3}{3\cdot2\cdot 1}=10よって,10通り。
Cの計算は,Pのように掛け算で代用できないので,しっかり覚えましょう。
Cで組合せが求められる理由
 学生の方
学生の方Pをr!で割るとCになるのはどうして?
_nC_r=\cfrac{_nP_r}{r!}になる理由が気になるアナタのために,ざっくりと説明しておきましょう。
例題で扱った5枚のカードで考えてみます。

5枚から3枚を取り出す組合せは_5C_3通りでした。
例えばこの中には(A,B,C)という組が存在します。
順番を考えない(_5C_3)ときは,(A,B,C)は1つの組でしかありません。
しかし,順番を考える順列(_5P_3)の場合は,1つの組(A,B,C)に対応する並び方が3!通り存在します。
これは(A,B,D)とか(C,D,E)とか,別の組についても同様です。
1つの組合せに対して,対応する並び替えが3!通りずつあります。
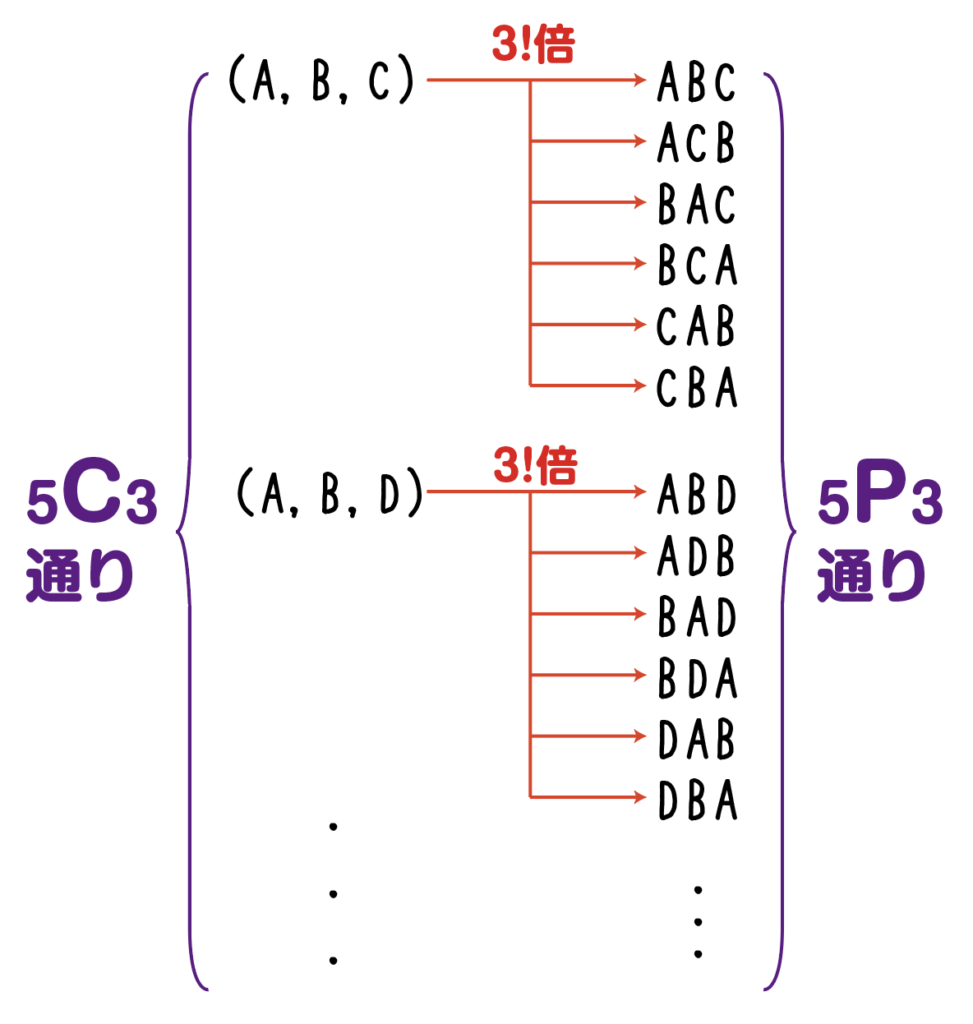
_5C_3を3!倍すると,_5P_3になる。つまり,
_5C_3\times 3!=_5P_3
となるので,両辺を3!で割って,
_5C_3=\cfrac{_5P_3}{3!}となります。
 粗茶さん
粗茶さん具体例で説明しましたが,一般の_nC_rについても成り立ちます。
Cの性質
組合せを表す_nC_rには,いくつかの重要な性質があります。
\begin{array}{l}
(1)_nC_0=1\\\\
(2)_nC_n=1\\\\
(3)_nC_r=_nC_{n-r}
\end{array}順に説明していきます。
(1)_nC_0=1
_nC_0は,「n個から0個を選ぶ選び方」ですが,
0個を選ぶということは,「何も選ばない」という1通りしかないので,
_nC_0=1 となります。
(2)_nC_n=1
_nC_nは,「n個からn個を選ぶ選び方」。
これもやはり「n個全部を選ぶ」という1通りしかないので,
_nC_n=1 となります。
(3)_nC_r=_nC_{n-r}
具体的に考えてみます。
n=5,r=2とすると,
_5C_2=_5C_3 です。
例えば,5人の応募者から合格者2人を選ぶ選び方は_5C_2通り。
一方,5人の応募者から不合格者3人を選ぶ選び方は_5C_3通り。
一見ちがって見えますが,結果として起こる状況って,同じですよね。
2人が合格して,3人が不合格。
実際に計算すればわかりますが,_5C_2と_5C_3は同じ値になります。
この性質を利用して,
Cの右下の数をなるべく小さくしたほうが,計算が楽になりますよ。
_{99}C_{97}の場合,
_{99}C_{97}=\cfrac{99\cdot 98\cdots3}{97\cdot 96\cdots 1}は,やってられないので,
_{99}C_{97}=_{99}C_{2}=\cfrac{99\cdot 98}{2\cdot 1}=99\cdot49=4851 ってやりましょう。
PとCの違いは「並べるか,並べないか」。
この記事では,P(順列)とC(組合せ)について,これらの違いと計算方法を紹介しました。
ざっくりまとめると,
- P(順列)はn個のものからr個選んで並べる方法の数。基本的には掛け算で代用。
- C(組合せ)は、n個からr個を選ぶだけの方法の数。計算方法は覚えること。
順列は「取り出して並べる」、組合せは「取り出すだけ」という違いをしっかりと理解して、場合の数の問題に自信を持って取り組みましょう。
特にCの計算は、場合の数や確率の単元で非常によく使われるので、しっかりマスターしておきましょう!

