自然数・整数・有理数・実数・複素数の記号と覚え方を考えてみた

学生の方

この前授業で先生が「xは自然数」っていうのを
x \in \mathbb{N}
って書いてたよ。
漢字書くの面倒だから、私もやりたい！

粗茶さん

動機がちょっと不純ですが、正しい記号法なので、紹介しましょう。

集合を表す記号は、ふつうはAやBなどを使います。

ですが、集合の中には、特別な記号で表されるものが存在します。

それが「自然数の集合」「整数の集合」「有理数の集合」「実数の集合」「複素数の集合」です。

これらの集合には、専用の記号が割り当てられています。

高校数学の教科書では扱われていないようですが、数学的には正しいので、知ってて損はないでしょう。

この記事では、自然数・整数・有理数・実数・複素数の集合を表す記号と、その語源や覚え方（？）を紹介します。

あなたも答案の中にさりげなく入れて、できる人を演出してみてはいかがでしょうか。

この記事を書いた人

粗茶

• 文系に特化して数学を分かりやすく教える高校数学の専門家
• 指導歴14年
• 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

一般的な集合の記号

数学の集合は、AやBなどの大文字を使って表します。

例えば、「xが集合Aに含まれる」ということは、

x \in A

と書きます。

このAの代わりに、ここで紹介する集合の記号を使うことで、「xは自然数」などの文を記号で表すことができます。

特別な集合を表す記号5つ

特別な集合を表す記号は、高校数学で扱う集合としては、次の5つがあります。

順に紹介していきますよ。

Nは自然数全体の集合

自然数全体の集合は、\mathbb{N}で表します。

自然数とは

自然数は、1,2,3,4,5,\cdotsのような、数を数えるときに使う数のことです。

正の整数というのも、自然数と同じ意味です。

高校（大学受験）までは、0は自然数に入りません。

粗茶さん

大学数学だと、0を自然数に入れることもあるそうです。

なぜ自然数がN？

自然数を英語で言うとnatural numberになるので、頭文字のNを使いました。

自然＝ナチュラルのNで覚えればよさそうですね。

Zは整数全体の集合

整数の集合は\mathbb{Z}で表します。

整数とは

整数は、小数点以下のない数のことです。

1,2,3のような正の整数もあれば、0も整数ですし、-1,-2,-3のような負の整数もあります。

なぜ整数がZ？

「数」をドイツ語で言うとZahlenになるので、頭文字をとってZです。

学生の方

ちょちょちょちょ、なんでドイツ語！？英語に統一しなさいよ！

整数を英語でいうとintegerなので、Iでもいいじゃないかと思うんですが、虚数を表すimaginary numberのIと勘違いしそうだからIは避けたと考えられています。

英語じゃないので覚え方が難しいですが、自然数のNを横に回転させるとZになるということで、整数は自然数の仲間だなあ。と覚えてはいかがでしょうか（強引にも程がある）

Qは有理数全体の集合

有理数全体の集合は\mathbb{Q}で表します。

有理数とは

有理数とは、\cfrac{\text{整数}}{\text{整数}}の形で表される数のことです。

整数も、例えは5は\cfrac{5}{1}とすれば分数の形になるので、有理数です。

また、有理数は、小数で表すと途中で終わる（有限小数）か、同じパターンを無限にくりかえす（循環小数）か、のどちらかになります。

ちなみに、有理数でない実数を無理数といいます。具体的には、ルートのついた数、\pi、eなどがあり、これらは小数点以下の数字がランダムに無限に続きます。

なぜ有理数がQ？

有理数は英語でrational numberなので、頭文字のRを使いたいところですが、

Rは後述する実数（real number）に使われてしまいまいした。

そこで、「割り算の商」を意味するquotientの頭文字でQが使われています。

「有理数はキュウリ数」とでも覚えましょう。

Rは実数全体の集合

実数全体の集合は\mathbb{R}で表します。

実数とは

実数とは、数直線上にある数のことを指します。

今までに出てきた、自然数、整数、有理数、無理数はすべて実数の仲間です。

実数は、2乗すると0以上になるという性質があります。

なぜ実数がR？

実数を英語で言うとreal numberになるので、頭文字のRを使いました。

実＝リアルのRでいいでしょう。

Cは複素数全体の集合

あまり使う機会がないですが、複素数全体の集合は\mathbb{C}で表します。

複素数とは

複素数は、\sqrt{-1}=iと定義したときに、a+bi（a,bは実数）で表される数です。

2+3iとか\cfrac{1}{\sqrt{3}}-5iみたいな感じです。

iが含まれている数を特に虚数といいます。

b=0のときは実数になるので、実数も複素数の仲間です。

なぜ複素数がC？

複素数は英語でcomplex numberなので、頭文字をとってCです。

実数と虚数のコンビのCとかで覚えましょう。

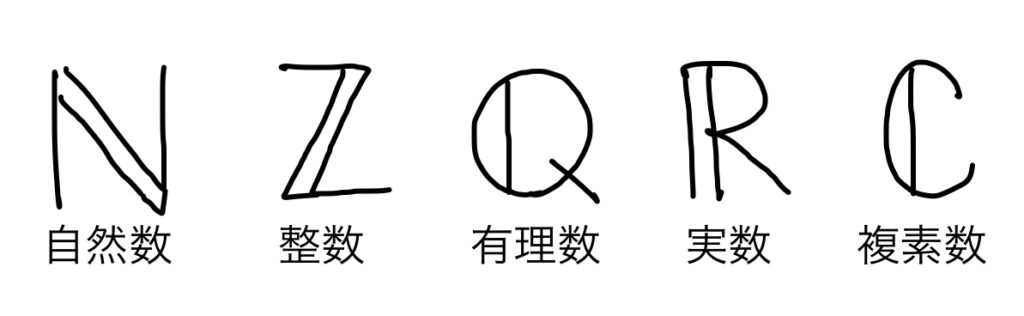
手書きの場合は、一部を二重線にする

手書きの場合は、一部を二重線にして、それっぽさを表現すればいいようです。

私が実際に書いた一例を示しておきます。

記号を使うと、「数学できてる感」が出せる

今回は、自然数・整数・有理数・実数・複素数の記号と覚え方を紹介しました。

もう一度まとめておくと、

「nは自然数」などは頻繁に登場するので、答案にさりげなく含めて、数学できてる感を演出するのも、悪くないかもね。