 学生の方
学生の方「2次方程式が1より大きい解をもつ」みたいな問題がよくわからなくて…。なんかグラフとか出てくるんだけど。
2次方程式が実数解を持つ条件といえば、判別式(D=b^2-4ac)の符号を調べればいいわけですが、
これが「1より大きい2つの実数解」とか「正の解と負の解を1つずつ」など、解に条件が追加されると、話は変わってきます。
このように、ある条件を満たす解をもつ条件を求める問題は、「解の配置」の問題と呼ばれたりします。
一見複雑そうに見える問題ですが、実は手順を一つだけ覚えてしまえば解けてしまいます。
この記事では、2次関数の「解の配置」問題を、複数のパターンを例に挙げて解説します。
 粗茶さん
粗茶さん複数のパターンと言いつつも、やり方は全部同じなんだけどね。
定期テストでは配点の高い問題として出題されることも多いので、しっかりマスターして周りと差をつけちゃいましょう!

粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

2次方程式の解は、2次関数のグラフとx軸との交点
そもそも2次方程式の解とは、2次関数のグラフとx軸との交点のx座標です。
例えば2次方程式
x^2+5x+6=0
の解は、
\begin{array}{ll}
(x+2)(x+3)=0\\\\
\therefore x=-2,-3
\end{array}となるわけですが,これは2次関数
y=x^2+5x+6
のグラフとx軸との交点のx座標でもありますよね。
具体的にはこんな感じ。
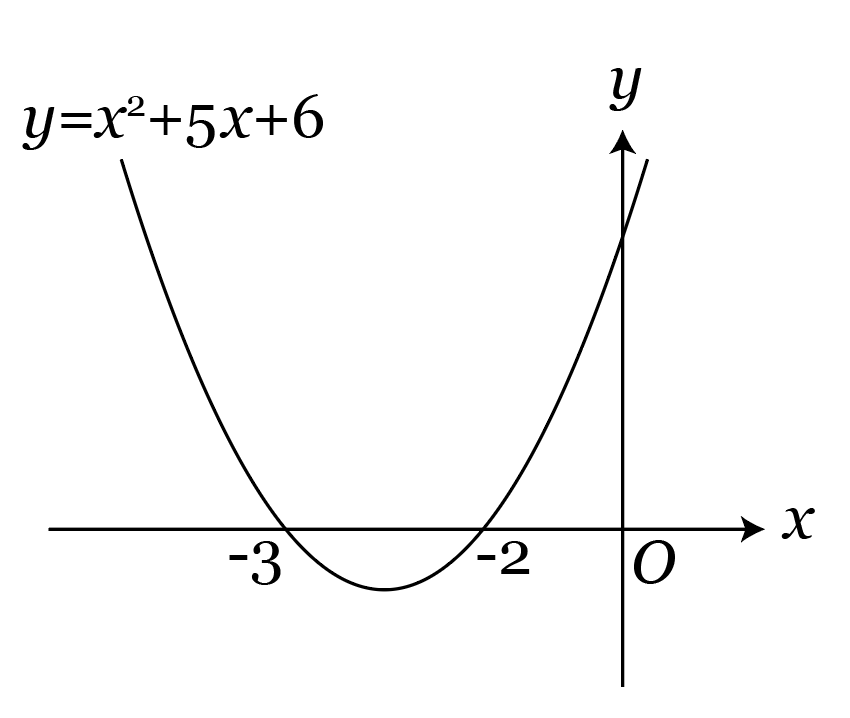
このようにして、2次関数のグラフを考えることが、解の配置問題では非常に大切になります。
解の配置問題でチェックするのは3項目
解の配置の問題をいくつか解いてみましょう。まずはこちらから。
xの2次方程式
x^2-2tx+3t=0
が、1より大きい異なる2つの解をもつとき、tの値の範囲を求めよ。
ただの「異なる2つの解」だけの問題だったら、「判別式D>0」で終わりなのですが、
「1より大きい」という条件が追加されると、話は変わってきます。
このような問題のときは、左辺をf(x)とおいて、y=f(x)のグラフが満たす条件を考えます。
チェックする項目は次の3つです。
- f(a)の符号
- 軸の位置
- 判別式の符号
必ず❶の「f(a)の符号」を最初に調べるようにします。
(❷と❸は逆でもいいです)
 粗茶さん
粗茶さん中には❶だけを調べればいい問題もあるんですよね。
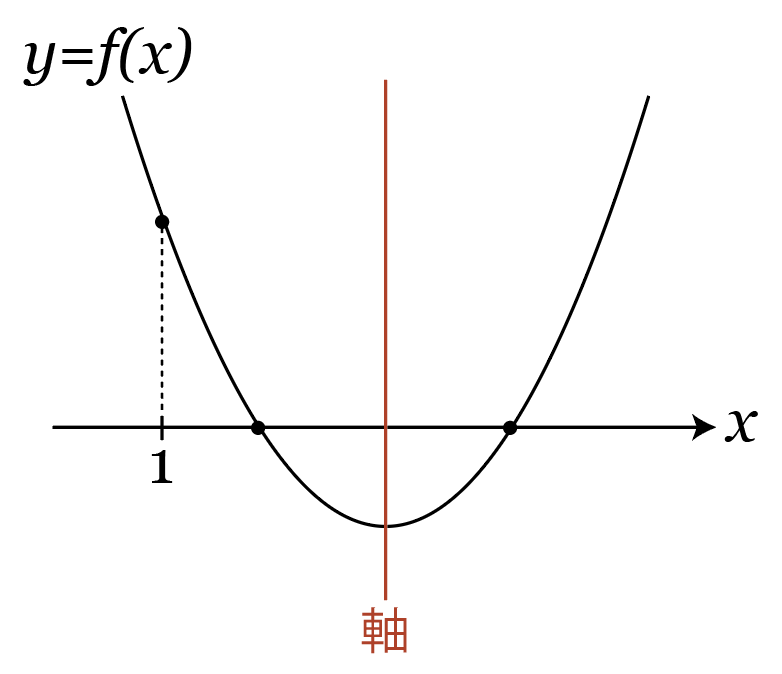
それでは解答に進んでいきますが、まずは問題に合うy=f(x)のグラフをつくると、こんな感じ。
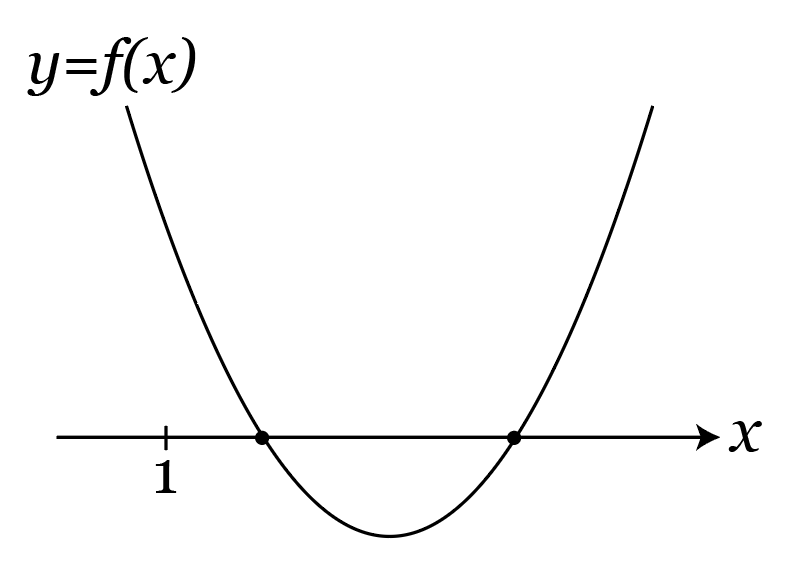
y=f(x)のグラフは、x軸のx\geqq 1の部分と異なる2点で交わります。
y=f(x)のグラフがこの形なる条件を作っていきましょう。
❶f(a)の符号
 学生の方
学生の方aって何?
とりあえずf(a)、つまりxにaを代入するということですが、
代入する数字は問題文に登場する数字だと思ってもらって構いません。
今回は「1より大きい解」という問題なので、f(x)にx=1を代入したときの符号を考えます。
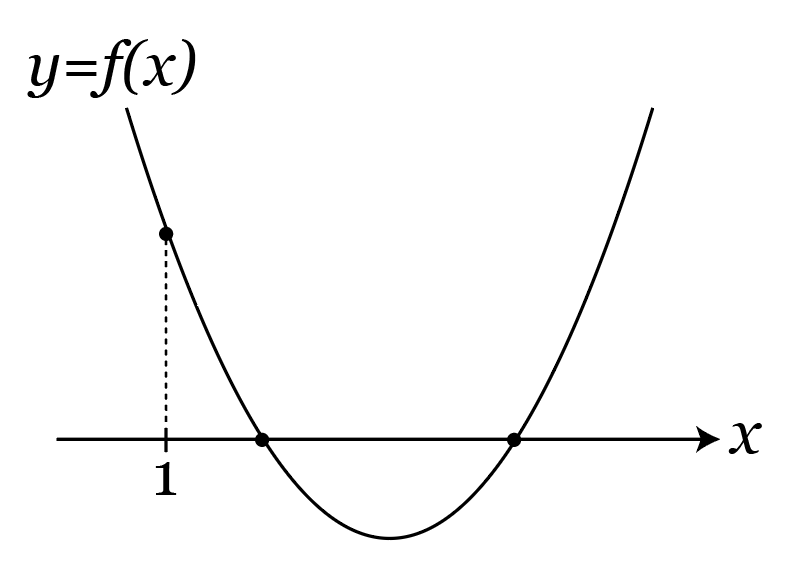
先ほどつくったグラフによると、x=1のときのy座標は正であることがわかるので、
f(1)>0\cdots ①
を満たすことがわかります。
❷軸の位置
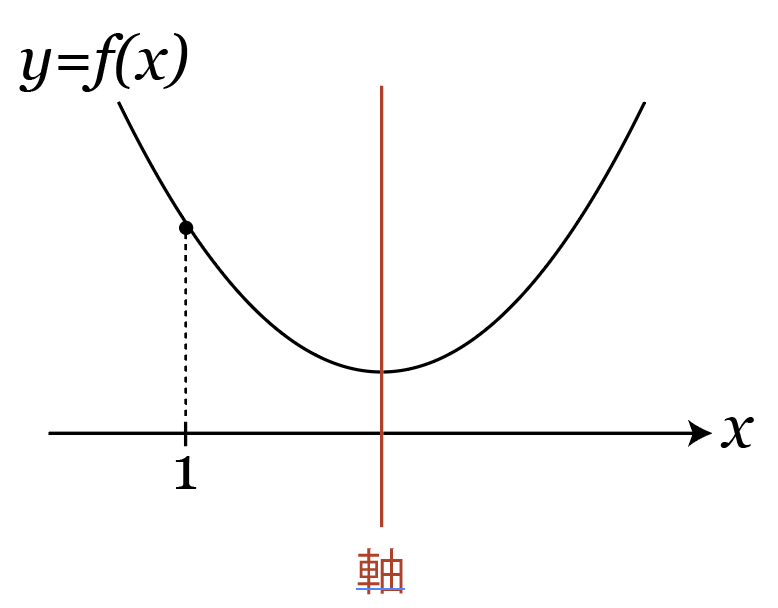
f(1)>0さえ満たしていれば、必ず目標とするグラフが描けるかというと、そうとは限りません。
例えば次のようなのはダメですよね?
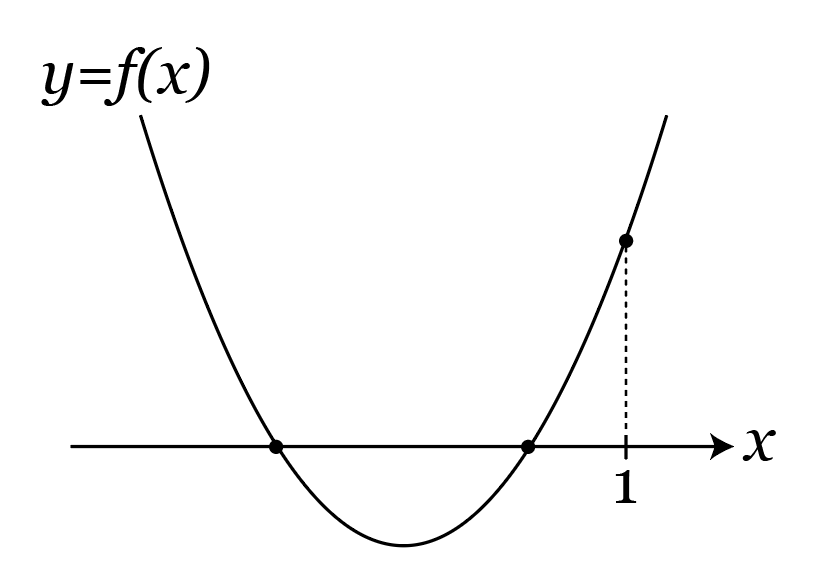
f(1)>0は満たしているものの、これだと「1より小さい2つの解」になってしまいます。
必ず1より大きい方で解をもってもらうために追加する条件が、「軸の位置」です。
f(1)>0であり、さらに
放物線の軸が1より右にあれば、
2つの交点も1より右になりますね。
ということで、2つめの条件は
(軸のx座標)>1\cdots②
ということになります。
❸判別式の符号
f(1)>0であって、かつ軸が1よりも右にあれば必ず「1より大きい異なる2つの解」になるかというと、もう1つ忘れてはいけないことがあります。
例えば次のようなのもダメですよね。
f(1)>0であって、かつ軸が1よりも右にあっても、そもそも実数解を持たないと始まりません。
ということで、3つ目の条件は、異なる2つの実数解をもつこと、つまり、
D>0\cdots③
 粗茶さん
粗茶さんDは判別式b^2-4acね。
です。
連立不等式を解く
ということで、今まで出てきた条件をまとめると、
\left\{
\begin{array}{ll}
f(1)>0&\cdots①\\\\
(軸のx座標)>1&\cdots②\\\\
D>0&\cdots③
\end{array}
\right.ということで、
これを連立不等式として解けば、条件を満たすtの範囲を求めることができます。
①を解く
①はf(x)に1を代入したものが正になります。
\begin{array}{ll}
&f(1)>0\\\\
&1^2-2t\cdot 1+3t>0\\\\
&1+t>0\\\\
\therefore&\color{red}t>-1
\end{array}②を解く
②は軸の位置なので、まずは軸を求める必要があります。
軸は平方完成ですね。
\begin{array}{rll}
f(x)&=&x^2-2tx+3t\\\\
&=&(x-t)^2-t^2+3t
\end{array}よって軸はx=tです。
これが1より大きくなればよいので、
\color{red}t>1③を解く
③は判別式が正。
\begin{array}{ll}
&D>0\\\\
&(-2t)^2-4\cdot 1\cdot 3t>0\\\\
&4t^2-12t>0\\\\
&t(t-3)>0\\\\
\therefore&\color{red}t<0 または 3< t
\end{array}共通範囲が答えになる
ここまでで求めた3つの不等式の共通部分が、求めるtの範囲になります。
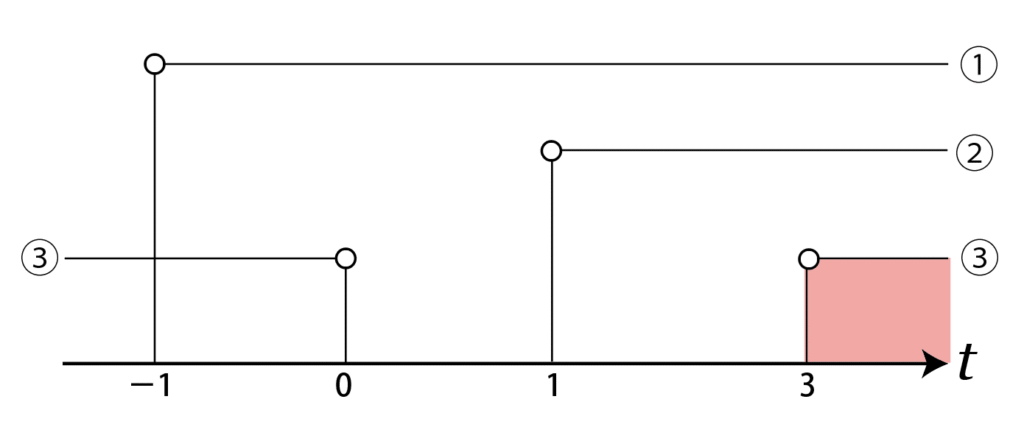
①かつ②かつ③より、求めるtの範囲は
\large t>3
となりました。
3項目とも調べなくていい場合もある
 学生の方
学生の方なんか問題によっては、不等式が1個で終わってるときもあったような…
実はこの解の配置問題、場合によってはf(a)の符号だけで終わる場合があります。
xの2次方程式
x^2-2tx+3t=0
が、1より大きい解と1より小さい解を1つずつもつとき、tの値の範囲を求めよ。
方程式は例題1と同じですが、今回は1より大きい解と1より小さい解をもつようです。
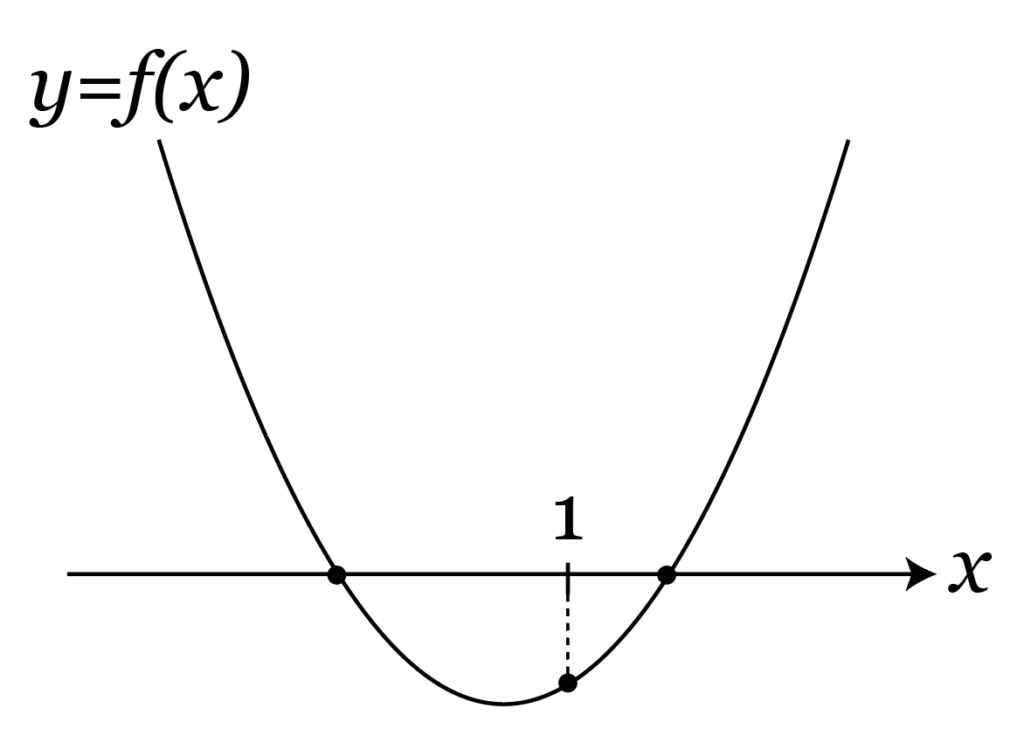
左辺をf(x)とすると、y=f(x)のグラフはこんな感じになりそうですね。
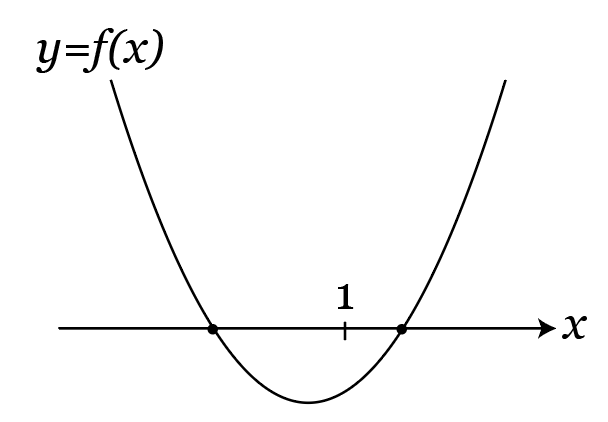
同様にして、このグラフになるようなtの条件を考えていきましょう。
❶f(a)の符号
やはり「1との大小」が問題になっているので、f(x)にx=1を代入したときの符号を考えます。
グラフによると、x=1のときのy座標は負であることがわかるので、
f(1)< 0
を満たすことがわかります。
❷軸の位置
次に軸の位置ですが、今回の場合、「軸が1より右にあるか左にあるか」は、条件を満たすかどうかとは関係がありません。
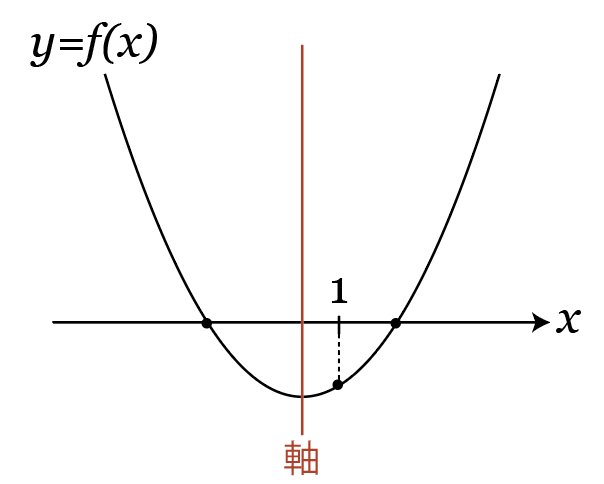
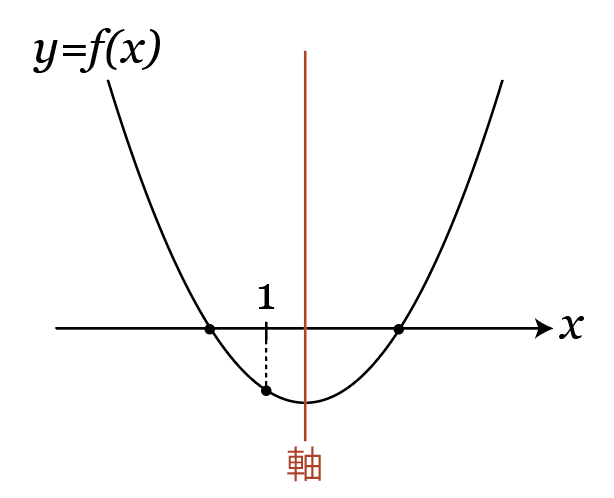
軸が1より右にあっても左にあっても、条件を成り立たせることは可能。
なので、軸の条件から不等式を作る必要はありません(というかできない)。
❸判別式の符号
3つめは判別式の符号でした。
例題1と同じように、異なる2つの実数解を持つ条件としてD>0を計算してもよいのですが、
そもそもf(1)<0を満たしながら、グラフとx軸の交点を1個や0個にすることはできないんです。
つまり、f(1)<0を満たしていれば、自動的にD>0も満たすことになるので、D>0を考える必要はありません。
 粗茶さん
粗茶さん考えてもいいんだけど、「D>0」は「f(1)<0」に完全に含まれるので、計算が無駄になっちゃうんですよね。
ということで、結局のところ求める条件は、
f(1)<0
の1つだけでOK。このまま解いていくと、
\begin{array}{ll}
&1^2-2t\cdot 1+3t<0\\\\
&1+t<0\\\\
\therefore&\large t<-1
\end{array}これが答えになります。
この例題のように、調べる3項目のうち❷と❸は考えなくてもいい場合がありますが、
❶のf(a)の符号は必ず考えることになるので、どんなタイプの問題であっても、f(a)の符号から考えると無駄が少なくすみますよ。
少し複雑な条件の問題にも慣れよう
ここまでのお話で、解の配置問題の基本的な問題を扱いました。
ここからはもう少し条件が複雑になった場合の問題も練習してみましょう。
xの2次方程式
x^2-2tx+3t=0
が、-2<x<5の範囲に異なる2つの実数解もつとき、tの値の範囲を求めよ。
例題1の少し応用バージョンです。
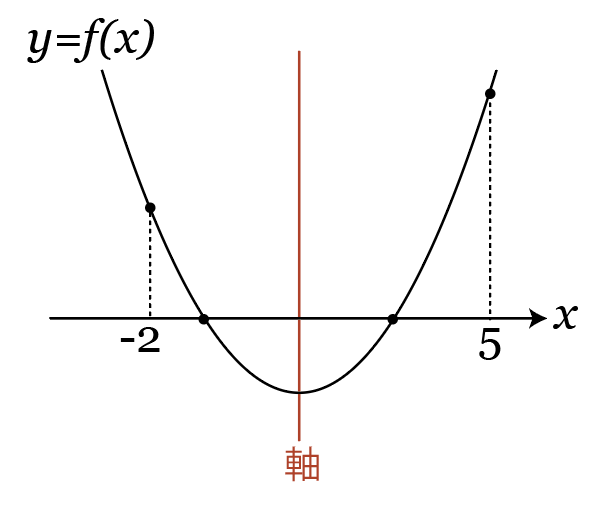
問題文に出てくる数字が-2と5の2つあるので、それぞれを代入したときの符号を条件にする必要があります。
❶f(a)の符号
まずはf(a)の符号。
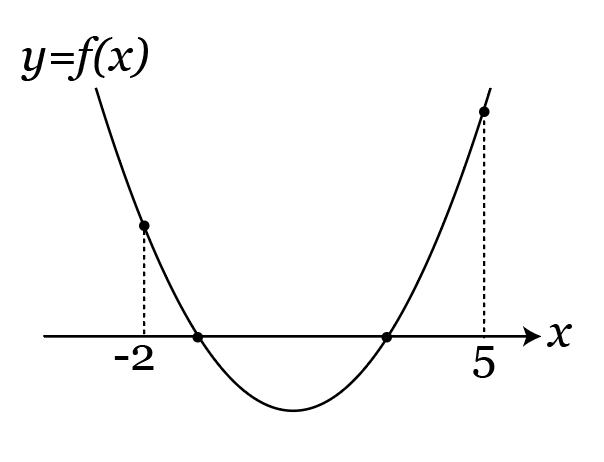
-2と5の間でグラフがx軸と2回交わるので、xに-2を入れても5を入れても、その値は正になります。つまり、
\begin{array}{ll}
f(-2)>0&\cdots①\\\\
f(5)>0&\cdots②
\end{array}を満たすことになります。
❷軸の位置
x軸の-2<x<5の部分でx軸と2回交わるためには、グラフの軸が-2<x<5の範囲にあることも必要。つまり、
-2<(軸のx座標)<5\cdots ③
が成り立ちます。
❸判別式の符号
3つめに考えるのは判別式の符号でしたね。
異なる2つの実数解なので、
D>0\cdots④
ということになります。
連立不等式を解く
ここまでの話で、求める不等式は、
\left\{
\begin{array}{ll}
f(-2)>0&\cdots①\\\\
f(5)>0&\cdots②\\\\
-2<(軸のx座標)<5&\cdots③\\\\
D>0&\cdots④
\end{array}
\right.の共通範囲ということになります。
①と②
まずは①を解きます。
\begin{array}{ll}
&f(-2)>0\\\\
&(-2)^2-2t\cdot (-2)+3t>0\\\\
&4+7t>0\\\\
\therefore&\color{red}t>-\cfrac{4}{7}
\end{array}続いて②も。
\begin{array}{ll}
&f(5)>0\\\\
&5^2-2t\cdot 5+3t>0\\\\
&25-7t>0\\\\
\therefore&\color{red}t<\cfrac{25}{7}
\end{array}③を解く
まずは軸を求めるます。平方完成ですね。
\begin{array}{rll}
f(x)&=&x^2-2tx+3t\\\\
&=&(x-t)^2-t^2+3t
\end{array}よって軸はx=tです。
これが-2と5の間にあればよいので、
\color{red}-2< t <5④を解く
④は判別式が正。ということで、
\begin{array}{ll}
&D>0\\\\
&(-2t)^2-4\cdot 1\cdot 3t>0\\\\
&4t^2-12t>0\\\\
&t(t-3)>0\\\\
\therefore&\color{red}t<0 または 3< t
\end{array}共通範囲が答え
①かつ②かつ③かつ④より、求めるtの範囲は
\color{red}-\cfrac{4}{7} < t < 0 または 3 < t < \cfrac{25}{7}まとめ
この記事では、2次方程式の解の配置問題の解き方を解説しました。
やることが多くて複雑に感じるかもしれませんが、
- f(a)の符号
- 軸の位置
- 判別式の符号
この3つを調べて、連立不等式を作ることができれば、意外と簡単です。
f(a)の符号を最初に調べることをお忘れなく!
このブログでは,自分で勉強しているとき,つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や,勉強が楽しくなる文房具も紹介していますので,よろしければご覧ください!



