学生の方高次方程式っていうのを習ったんだけど、いまいち解き方がわかんなくて…
何か解を見つける、みたいなことを言ってた気がするんだけど…
一般に3次以上の方程式のことを高次方程式といいます。
3次以上といってもいくつかの種類がありますが、この記事では最も一般的な、因数分解の公式や置き換えなどが使えないパターンの方程式を扱います。
高次方程式を解く手順は、
- 解を1つ見つける
- 割り算をして因数分解
- 解く
という流れになります。
この中でも最初の解を見つけるところと、割り算が手間だと思います。
実は、解を見つけるときにはちょっとしたコツがあるし、割り算をしなくても因数分解できる方法があります。
この記事を読めば、高次方程式を解くスピードが格段に上がること間違い無し！
高次方程式の解き方の手順を解説！
それではさっそく、高次方程式の解き方を手順を解説していきます。
この問題でやってみましょう。
xの方程式
x^3−6x^2+11x−6=0
を解きなさい。
高次方程式の解く手順①解を見つける
高次方程式を解くためには、まず最初に解を1つ見つける必要があります。
見つける方法自体はとてもシンプルで、xに数字を代入して、0になるかどうかを試します。
1から順に代入してみて、0になったとき、それが解の1つということです。
学生の方えー、めんどくさい…
粗茶さんここはどうしようもないので、我慢してください…
とりあえず、左辺に1を代入してみると、
\begin{array}{r}
1^3-6\cdot 1^2+11\cdot 1-6=0
\end{array}って、見事に0になったので、x=1はこの方程式の解だということがわかりました。
学生の方でも、いつも1が解ってことはないじゃん？
なんか効率よく探す方法とかないの？
粗茶さん1つずつ代入して試すことは変わらないけど、解の候補となる数字には限りがあるよ。
高次方程式の解は、
\pm\cfrac{定数項の約数}{最高次の項の係数の約数}が候補。
今回の例題だと、定数項は－6、最高次（x^3）の係数が1なので、解の候補は、
1, -1, 2, -2, 3, -3, 6, -6
の8個ということです。
なので、この候補にない4とか5とかが解になることはありえないので、代入して確かめる必要はないよ。ということになります。
粗茶さん結局は0になるまで地道に確かめるしかないんですよね…
実際、全然見つからなくて-3しか解がなかった！という事例も報告されているので、ここは頑張るしかないですね。。
高次方程式を解く手順②(x-a)で割って因数分解する
方程式の解がx=1になるということは、この方程式は、
(x-1)( ・・・・)=0
っていう形に、左辺が因数分解されるはずです。
つまり、x=1が解ならば、左辺はx-1で割り切れるってことになります。
ということで(x^3−6x^2+11x−6)÷(x-1)をすればいいのですが、割り算をするのも結構面倒なので、私がおすすめするのは、
展開して元に戻る式を考える
という方法です。
これは動画を作りましたので、こちらを観ていただくのが早いかと思います。
文章で説明すると次のようになります。
3次式を1次式で割ると、2次式になるので、右側のカッコの中は2次式になり、方程式はこんな形になります。
(x-1)(ax^2+bx+c)=0
このa,b,cを求めることになりますが、左辺を展開してx^3-6x^2+11x-6になればいいので、実はaとcはすぐにわかります。
まず、展開してx^3の項になるのは、x\cdot ax^2=ax^3しかありません。
そして、このax^3が元の左辺のx^3と一致すればよい。
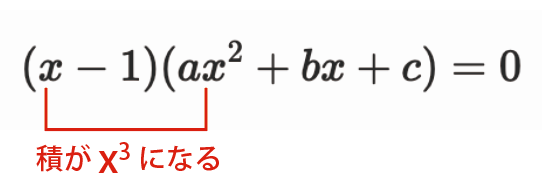
ということで、aは1になります。
次に、展開して定数項になるのは、-1\cdot c=-cしかない。
この-cが元の左辺の定数項-6と一致するので、
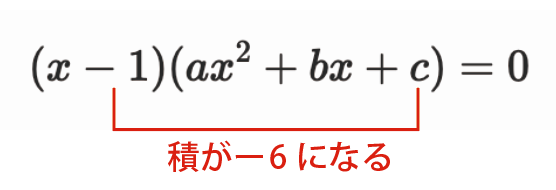
cは6に決まります。
ここまでで、b以外はわかりました。
(x-1)(x^2+bx+6)=0
真ん中のbを求めるには、展開してx^2になる項かxになる項のどちらかに注目します。
展開してx^2になる項は、x\cdot bx=bx^2と、-1\cdot x^2=-x^2の2つがあります。
この2つを足し合わせると(b-1)x^2となり、これが元の左辺の-6x^2と一致すればよいので、
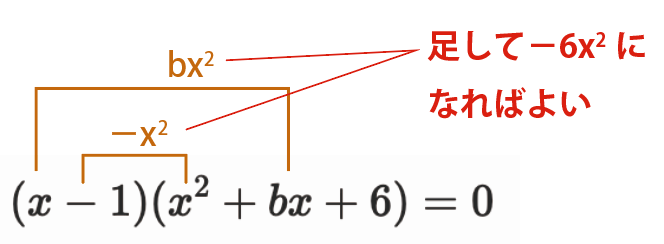
係数を比較して、
b-1=-6 \therefore b=-5
となります。
展開してxになる項に注目してもOK。
展開してxになる項は、x\cdot 6=6xと、-1\cdot bx=-bxの2つがあります。
この2つを足し合わせると(6-b)xとなり、これが元の左辺の11xと一致すればよいので、
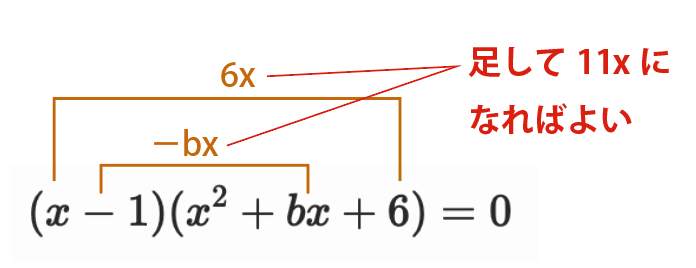
係数を比較して、
6-b=11 \therefore b=-5
どちらの方法でも、bは－5だとわかりました。
ということで、左辺の因数分解は次のようになります。
(x-1)(x^2-5x+6)=0
高次方程式を解く手順③「それぞれのカッコ内の式=0」を解く
ここまでできれば、あとは普通に解くだけ！と言っていいと思います。
(x-1)(x^2-5x+6)=0
なので、
x-1=0\cdots①
と、
x^2-5x+6=0\cdots②
の2つを解きます。
①から、
x=1
②はさらに因数分解できて、
(x-2)(x-3)=0
になるので、
x=2, 3
ということで、方程式全体の解は、
x=1,2,3
となりました。
ちなみに今回のように②の部分が因数分解できる場合は、先に
(x-1)(x-2)(x-3)=0
ってやってしまった方がいいかもしれませんね。
高次方程式の練習問題
高次方程式の解き方がわかったところで、少し練習問題をやってみましょう。
負の解が見つかったときは符号に注意
xの方程式
x^3-2x^2-11x-6=0
を解きなさい。
まずは解を見つける作業からです。最高次の係数が1、定数項が-6なので、例題1と同じで解の候補は
1,2,3,6,-1,-2,-3,-6
のどれかになります。色々試した結果、今回は
(-2)^3-2\cdot(-2)^2-11\cdot(-2)-6=0
だけが成り立つので、x=-2が解ということになります。
ということは左辺はx{\color{red}+}2で割り切れます。
x=aが解のときにx-aで割り切れるんだったので、
x=-2が解のときはx-(-2)=x+2で割り切れるということに注意しましょう。
それでは実際に割っていきましょう。
3次式を1次式で割ると2次式になるので、左辺は
(x+2)(ax^2+bx+c)=0
って因数分解できるはずです。
左辺を展開してもとのx^3-2x^2-11x-6になればOK。
展開するとx^3の項はax^3で、これが元の左辺のx^3と一致するとき、
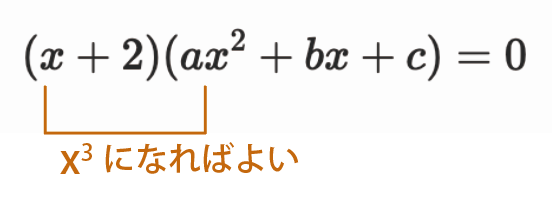
a=1とわかります。
次に、展開したときの定数項は2cで、元の定数項は6なので、
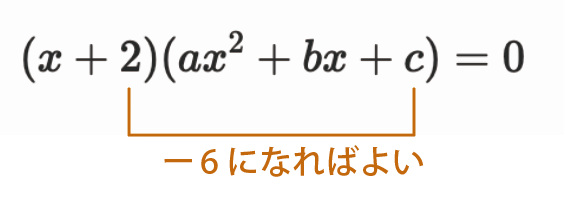
2c=-6より、c=-3になります。
ここまでで、b以外がわかりました。
(x+2)(x^2+bx-3)=0
bについては、x^2の項かxの項に注目します。
（ここではx^2の方でやります）
展開してx^2になるのは、x\cdot bx=bx^2と、2\cdot ax^2=2ax^2の2項があります。
これらを足した(b-2)x^2が、もとの左辺の-2x^2と一致すればいいので、
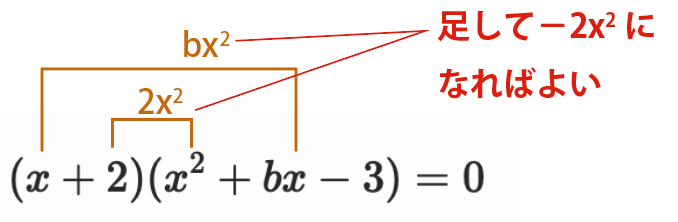
係数を比較して、b-2=-2よってb=-4となります。
よって左辺を因数分解すると、
(x+2)(x^2-4x-3)=0
となります。
最後にそれぞれのカッコ内が0になるxを求めます。つまり、
x+2=0\cdots①
と、
x^2-4x-3=0\cdots②
を解けばよいです。
①から、
x=-2
②は因数分解できないので解の公式で、
x=\cfrac{-(-4)\pm\sqrt{(-4)^2-4\cdot 1\cdot (-3)}}{2\cdot 1}=\cfrac{4\pm2\sqrt{7}}{2}=2\pm\sqrt{7}ということで、この方程式の解は、
x=-2，2\pm\sqrt{7}となりました。
流れは例題1と同じですが、負の解が見つかった場合は、割る式の符号を間違えやすいので注意しましょう。
まとめ
高次方程式は一見難しそうに見えますが、正しい手順を踏めば誰でも解けるようになります。
まずは「解をひとつ見つける」ところからスタートし、それを手がかりに式を分解しながら簡単な形にしていきます。
その中で大事なのは、数字を代入して確認するだけでなく、「解の候補をあらかじめ絞るテクニック」や「因数分解の考え方」をしっかり理解しておくことです。
今回紹介したような手順を身につけておけば、今後どんな高次方程式が出てきても慌てずに対応できるようになります。
「高次方程式って難しい」という印象を払拭して、自信を持って問題に取り組んでいきましょう！