 学生の方
学生の方微分で接線の方程式を求めるっていうのがあるんだけど、よくわからないんだよね…
数IIの最後の単元「微分・積分」。
微分の計算なんかは公式通りで簡単ですが、接線の方程式を求めるあたりからつまずいているのではないでしょうか?
実は接線の方程式も、普通の直線の方程式も、基本的な考え方は同じです。
この記事では、数IIの微分で出てくる接線の方程式の求め方をわかりやすく説明していきます。
接線の求め方は微分の中では基本でありながら超重要なので、しっかりマスターしましょう!

粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

基本は直線の方程式
接線も直線であることには変わりないので、直線の方程式の求め方を使います。
 学生の方
学生の方直線の方程式って、どうやるんだっけ?
直線は、傾きと通る点が決まれば、1つに決まります。
こんな公式がありましたね?
傾きが\color{red}aで、点({\color{blue}p}, {\color{green}q})を通る直線の方程式は、
y-{\color{green}q}={\color{red}a}(x-{\color{blue}p})この公式に傾きと通る点の座標を当てはめれば、直線の方程式が作れます。
少し練習を。
(1)傾きが2で点(1,3)を通る直線の方程式は?
(2)2点A(3,-8), B(6,1)を通る直線の方程式は?
(1)は公式そのままでいけますね。
傾きが2で点(1,3)を通るので、公式に当てはめて、
\begin{array}{ll}
y-{\color{green}3}={\color{red}2}({\color{blue}x}-1)\\\\
\therefore y=2x-1
\end{array}(2)は傾きが書かれていないので、2点の座標から傾きを求めます。
 粗茶さん
粗茶さん直線の傾きは\dfrac{yの増加量}{xの増加量}でしたね。
この直線の傾きは、\dfrac{1-\left( -8\right)}{6-3}=3なので、
求めるものは、傾き3で(6, 1)を通る直線である。
 粗茶さん
粗茶さん点は(1,-8)を使ってもOK。計算が簡単な方を選ぼう。
ということで、
\begin{array}{l}
y-{\color{green}1}={\color{red}3}(x-{\color{blue}6})\\\\
\therefore y=3x-17
\end{array}微分を使って求める接線の方程式も、基本は通常の直線の求め方と同じ!
ということをしっかり頭に入れておきましょう。
微分とは「接線の傾き」
 学生の方
学生の方f’(x)みたいな微分の計算は簡単だからできるんだけど、微分って結局何なの?
微分は「接線の傾き」のことだと思ってもらって、基本的にはOKかと思います。
もう少し細かく言うと、微分した式のxに接点のx座標を代入すると、その点での接線の傾きが求められるということになります。
微分の公式(導関数の求め方)を確認しておくと、
x^nの導関数はnx^{n-1}
であり,「導関数を求めること」を「微分する」という。
また、xの式f(x)の導関数をf’(x)と書く。
例を少し紹介すると、
\begin{array}{llll}
①&f(x)=x^2+3x+5&のとき,&f’(x)=2x+3\\\\
②&f(x)=2x^3+5x^2+x+4&のとき,&f’(x)=6x^2+10x+1
\end{array}みたいな感じですね。
この微分自体は問題なくできると思います。
で、このf’(x)のxに接点のx座標を代入すると、その点における接線の傾きが求められます。
傾きが分かれば、あとは直線の方程式を求める要領で接線の方程式が求められますよ。
接線の方程式(接点がわかってる場合)
ここからは、実際に微分を使って接線の方程式を求めてみましょう。
まずはこんな問題からどうぞ。
2次関数y=x^2+2x+1上の点(1,4)における接線の方程式を求めよ。
「〜上の点(1,4)における接線」といわれているときは、この点(1,4)は接点になっています。
イメージはこんな感じです。
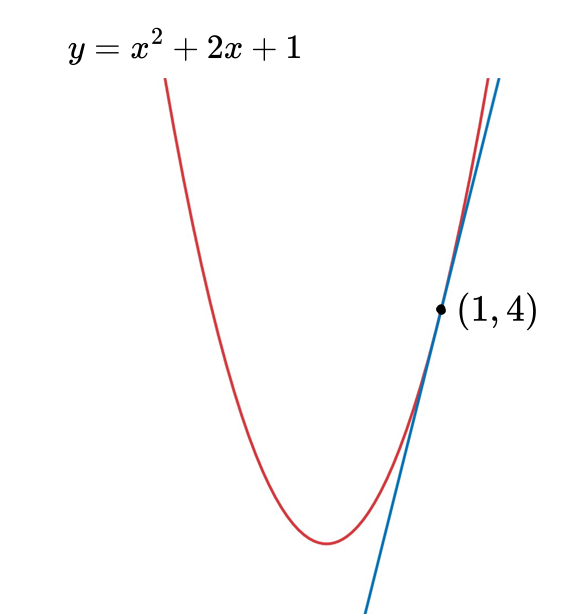
求める接線が点(1,4)を通ることはわかっているので、あとは傾きを求めればOK。
ここで微分を使います。
y=x^2+2x+1より,y’=2x+2
x=1を代入して,接線の傾きは、
2\cdot 1+2=4
よって求める接線は、傾きが4で点(1,4)を通る直線なので、
\begin{array}{l}
y-4=4(x-1)\\\\
\therefore y=4x
\end{array}ということなります。
傾きを求めるところで微分を使う以外は、ふつうに直線を求める問題と同じだということを理解してくださいね。
接線の方程式(接点がわからない場合)
続きまして、こんな問題も頻出です。先ほどとの違いに注目しましょう。
2次関数y=x^2-x+3に点(1,-1)から引いた接線の方程式を求めよ。
 学生の方
学生の方さっきと同じじゃないの?
この点(1,-1)は、y=x^2-x+3の上にはない、つまり接点ではありません。
接線の方程式を求める問題の中には、このように接点が書かれていない場合もあります。
でも接線の傾きを求めるためには、接点の座標がなくてはなりません。
 学生の方
学生の方接点がわかってないのに接点が必要って、もう詰んでるんじゃ…
接点がわかっていない場合は、とりあえず接点のx座標をtとおいて、接線の式をtで表すことを考えましょう。
y=x^2-x+3 より,y’=2x-1
接点の座標を(t,t^2-t+3)とおくと,接線の傾きは,
2t-1
求める接線は傾き\color{red}2t-1で点({\color{blue}t},{\color{green}t^2-t+3})を通るので、
\begin{array}{l}
y-({\color{green}t^2-t+3})=({\color{red}2t-1})(x-{\color{blue}t})\\\\
\therefore y=(2t-1)x-t^2+3\cdots①
\end{array}これで、とりあえず接線の式ができました。
さらにtを求めなければいけませんが、そこで登場するのが問題文にある点(1,-1)です。
求める接線は、点(1,-1)から放物線に引いた線、つまり図にするとこんな感じになるので、

求める接線は点(1,-1)を通る、つまり(1,-1)を代入して成り立つということです。
これでtがわかって,接線も求められるわけですね。
①は点(1,-1)を通るので、
\begin{array}{rcl}
-1&=&(2t-1)\cdot1-t^2+3\\\\
t^2-2t-3&=&0\\\\
(t+1)(t-3)&=&0\\\\
\therefore t&=&-1,3
\end{array} 学生の方
学生の方tが2つ出てきたっていうのは、どういうこと?
放物線の上にない点から引いた接線は、1本とは限りません。
さっきの図では1本しか引かなかったですが、実はもう1本の接線があるのです。

接線が2本書けるときは、2本とも答えるようにします。
t=-1のとき、①に代入して、
y=-3x+2
t=3 のとき、①に代入して、
y=5x-6
以上より、求める接線は
y=-3x+2,y=5x-6
このように、接点がわかっていない問題では、とりあえず接点をtとおく!と覚えておきましょう。
まとめ
それでは、今回のお話をまとめておきますね。
- 接線に限らず、直線を求めるには「傾き」と「通る点」が必要。
- 接線の傾きは微分を使って求める。
- 接点がわかってる場合→微分して接点のx座標を代入。
- 接点がわかってない場合→仮の接点を(t,f(t))とおく。
接線の方程式は数学Ⅱの中でも重要な単元ですが、基本をしっかり押さえれば、どんな問題にも対応できます。
今回の内容をしっかり理解し、例題を解いて実践的に学ぶことで、苦手意識をなくしましょう!

