 学生の方
学生の方二項定理って,Cとか出てきてよくわかんないんだけど,結局なんなの?
数IIで習う「二項定理」。
「見たことあるけど意味はわかってない…」と思っていませんか?
この記事では、二項定理の基本から式にCが出てくる理由、さらに二項定理を用いた係数の問題までを解説します。
これを読めば、二項定理の基本的な問題を得点源にできますよ。

粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

二項定理は(a+b)のn乗の展開
二項定理とは,早い話が(a+b)^nを展開した式のことです。
中学校からやってる式の展開で,こういうのがあるでしょ?
\begin{array}{lll}
(a+b)^2&=&a^2+2ab+b^2\\\\
(a+b)^3&=&a^3+3a^2b+3ab^2+b^3
\end{array}3乗までは暗記した人も多いと思いますが、何乗であっても、次の式に当てはめることで、展開の式を作ることができます。
(a+b)^n=_nC_0a^n+_nC_1a^{n-1}b^1+_nC_2a^{n-2}b^2+\cdots +_nC_ra^{n-r}b^r+\cdots+_nC_nb^n実際にnに数字を当てはめて考えてみると、
n=2の場合、
\begin{array}{lll}
(a+b)^2&=&_2C_0a^2+_2C_1a^{2-1}b^1+_2C_2b^2\\\\
&=&a^2+2ab+b^2
\end{array}n=3の場合、
\begin{array}{lll}
(a+b)^3&=&_3C_0a^3+_3C_1a^{3-1}b^1+_3C_2a^{3-2}b^2+_3C_3b^3\\\\
&=&a^3+3a^2b+3ab^2+b^3
\end{array}ちゃんと公式の通りになっていますね!
4乗以降も同じように求めることができますよ。
二項定理の展開にCが出てくる理由
 学生の方
学生の方でも、どうしてCを使うと係数がわかるの?
確かに突然Cが出てくるのには違和感があるかもしれません。
それでは、二項定理にCが出てくる仕組みを説明していきますよ。
今回は3乗の展開で説明しますね。
(a+b)^3は、(a+b)を3回かけるということなので、横に3つの(a+b)を並べて1つずつ展開することでも計算できますよね。こんな感じで。
(a+b)^3=(a+b)(a+b)(a+b)
それぞれの括弧に①、②、③と番号をつけると、
- ①からaとbのどちらかを選び
- ②からaとbのどちらかを選び
- ③からaとbのどちらかを選び
これら3つをかける
ことによって、1つの項ができあがります。

これを重複なくすべてのパターンで行って、同類項をまとめると、展開式が完成となります。
ここで例えばa^2bの項について考えると、
- ①のa、②のa、③のbをかけてa^2b
- ①のa、②のb、③のaをかけてa^2b
- ①のb、②のa、③のaをかけてa^2b
という3つがあるので、最終的に{\color{red}3}a^2bになります。

実は、この係数を組合せ(C)で求めることができるんです。
a^2bの場合だと、①②③のうち、bを取る括弧を1つ選べば、自動的に残りの括弧からはaが選ばれるので、a^2bの係数は、①②③の3つの括弧からbを取る括弧を1つ選ぶ選び方の数と同じで、それはまさに
_3C_1=3
ということになります。
また、b^3の場合を考えると、①②③のうち、3つすべての括弧からbを取ることでb^3になるので、
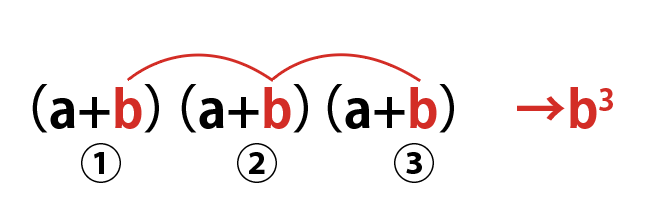
b^3の係数は、①②③の3つの括弧からbを取る括弧を3つ選ぶ選び方の数と同じで、それは、
_3C_3=1
ですよね。
このように、「どの括弧からaを取って、どの括弧からbを取るか」の組合せの数が係数になるんですね。
ちょっと例題をやってみましょう。
次のものを求めなさい。
(1)(a+b)^4を展開したときのa^2b^2の係数
(2)(a+b)^{12}を展開したときのa^8b^4の係数
何乗になっても、「どの括弧からaを取って、どの括弧からbを取るか」の組合せの数を求めればOK。
(1)は、4つの括弧のうち、bを取る括弧を2つ選ぶので、
_4C_2=\cfrac{4\cdot3}{2}=6(2)は、12個の括弧のうち、bを取る括弧を4つ選ぶので、
_{12}C_4=\cfrac{12\cdot 11\cdot 10\cdot 9}{4\cdot 3\cdot 2}=495 粗茶さん
粗茶さんここまで「bを取る括弧」の選び方で計算してますが、「aを取る括弧」の選び方でやっても同じ答えになります。(2)だと_{12}C_8=495。
二項定理の一般項と係数の問題
二項定理の問題といえば、一番よく出てくるのが係数を求める問題です。
係数の問題では、二項定理の一般項を使うことで、機械的に計算することができます。
(a+b)^nの展開式の一般項は
\large _nC_ra^{n-r}b^r(ただし0\leqq r\leqq n)
二項定理で展開したすべての項は、_nC_ra^{n-r}b^rの形をしています。
例えば、n=4の場合、4乗の展開になって、一般項は、
_4C_ra^{4-r}b^rってなります。
ここで、a^2b^2の項を知りたいなと思ったら、r=\color{red}2とすれば、
_4C_{\color{red}2}a^{4-{\color{red}2}}b^{\color{red}2}=\cfrac{4\cdot 3}{2}a^2b^2=6a^2b^2のようにして求めることができます。
一般項をつくって係数を求める
(2x^2+y^3)^5を展開した式のx^6y^6の係数を求めよ。
少し複雑になっていますが、2x^2=a,y^3=bとみれば、(a+b)^5の形になっています。
展開式の一般項は、
_5C_r(2x^2)^{5-r}(y^3)^r 粗茶さん
粗茶さん_5C_ra^{5-r}b^rのaが2x^2,bがy^3に変わりました。
これを数字の部分と文字の部分に分けます。
\begin{array}{ll}
&_5C_r(2x^2)^{5-r}(y^3)^r\\\\
=&_5C_r\cdot2^{5-r}\cdot(x^2)^{5-r}\cdot y^{3r}\\\\=&_5C_r\cdot2^{5-r}\cdot x^{\color{blue}10-2r}\cdot y^{\color{green}3r}
\end{array} 粗茶さん
粗茶さん_5C_rは計算すれば最終的に数字になりますね。
x^6y^6の項は、{\color{blue}10-2r}=6 かつ {\color{green}3r}=6 のときで、r=\color{red}2だとわかる。
先程の式に代入して、x^6y^6の項は、
\begin{array}{ll}
&_5C_{\color{red}2}\cdot 2^{5-\color{red}2}\cdot x^{10-2\cdot {\color{red}2}}\cdot y^{3\cdot{\color{red}2}}\\\\
=&\cfrac{5\cdot 4}{2}\cdot 2^3\cdot x^6y^6\\\\
=&80x^6y^6
\end{array}よって、求める係数は\large{80}
こんな感じで、一般項をつくって、適切なrを代入すれば求められます。
もう一つ問題をどうぞ。
\left(2x^2-\cfrac{1}{x}\right)^7の展開式におけるx^5の項の係数を求めよ。
2x^2=a,-\cfrac{1}{x}=bとみれば、(a+b)^7の形になっています。
マイナスになってることに注意しましょう。
展開式の一般項は、
\begin{array}{ll}
&_7C_r(2x^2)^{7-r}\left(-\cfrac{1}{x}\right)^r\\\\
=&_7C_r2^{7-r}(x^2)^{7-r}(-1)^r\left(\cfrac{1}{x}\right)^r\\\\
=&_7C_r2^{7-r}(-1)^r\cfrac{x^{14-2r}}{x^r}\\\\
=&_7C_r2^{7-r}(-1)^rx^{\color{blue}14-3r}\\\\
\end{array} 粗茶さん
粗茶さん\cfrac{x^{14-2r}}{x^r}=x^{14-2r-r}=x^{14-3r}です。
x^5の項は、{\color{blue}14-3r}=5のときで、r=3
これを代入して、x^5の項は、
\begin{array}{ll}
&_7C_{\color{red}3}2^{7-{\color{red}3}}(-1)^{\color{red}3}x^{14-3\cdot{\color{red}3}}\\\\
=&\cfrac{7\cdot 6\cdot 5}{3\cdot 2}\cdot 2^4\cdot(-1)x^5\\\\
=&35\cdot 16\cdot(-1)x^5\\\\
=&-560x^5
\end{array}よって、求める係数は\large{-560}
(a+b+c)のn乗の展開式
括弧の中が3つの項になっている場合の展開式についても扱います。
(a+b+c)^nの展開式の一般項は次のようになります。
(a+b+c)^nの展開式の一般項は、
\large_nC_p\cdot {_{n-p}C_q}\cdot a^pb^pc^r(ただしp,q,rは負でない整数で、p+q+r=nを満たす)
3項の場合でも、それぞれの括弧からa,b,cを1つずつ取ってかけると1つの項ができあがりますね。
例えば(a+b+c)^5について、a^2b^2cであれば、5つの括弧のうち2つからa、残り3つの括弧のうち2つからbを選ぶと、自動的に残った括弧からcを選び、この5文字をかけることでできあがります。
「どの括弧からどの文字を選ぶか」の選び方は複数パターンありますよね。
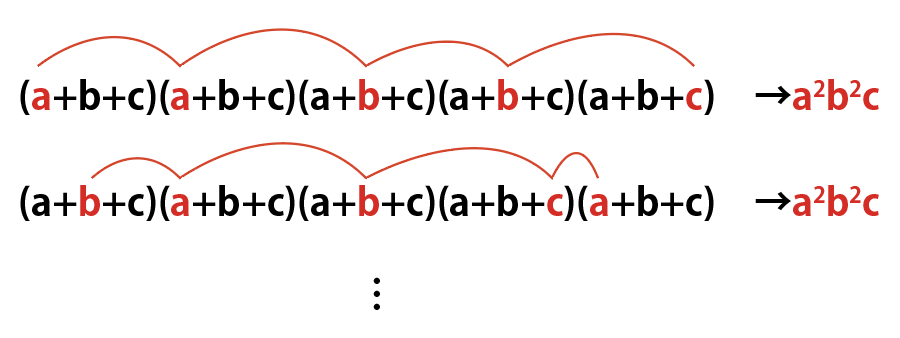
このa,b,cの選び方の個数が、a^2b^2cの係数になるわけです。
なので、(a+b+c)^5の展開式のa^2b^2cの係数は、
5つの括弧の中からaを取る括弧の選び方が_5C_2通り、
それぞれに対して、残り3つの括弧の中からbを取る括弧の選び方が_3C_2通り、
残った括弧からは自動的にcが選ばれる
ということで、求める係数は
_5C_2\cdot _3C_2=30
となります。
これを一般項の形にすると、上で書いた
_nC_p\cdot_{n-p}C_q\cdot a^pb^qc^rということになります。
「同じものを含む順列」の公式の考え方で、
\cfrac{n!}{p!q!r!}a^pb^qc^rとしても同じ計算になります。
(x-2y+3z)^5の展開式におけるx^2yz^2の項の係数を求めよ。
a=x,b=-2y,c=3zと置けば、(a+b+c)^5の形です。
展開式の一般項は、
_5C_p\cdot _{5-p}C_q\cdot x^p\cdot(-2y)^q\cdot(3z)^r=_5C_p\cdot _{5-p}C_q\cdot(-2)^q\cdot 3^r\cdot x^py^qz^r(ただしp,q,rは負でない整数で、p+q+r=nを満たす)
x^2yz^2の項は、p=2,q=1,r=2のときなので、求める係数は、
\begin{array}{ll}
&_5C_2\cdot_{5-2}C_1\cdot(-2)^1\cdot 3^2\\\\
=&_5C_2\cdot_3C_1\cdot(-2)\cdot 9\\\\
=&10\cdot 3\cdot(-2)\cdot 9\\\\
=&-540
\end{array}一般項を作ったあとの考え方は、2項の場合と同じ感じですね。
ではもう一つ例題を。同じように見えますが…
(x^2-2x+3)^5の展開式におけるx^4の係数を求めよ。
a=x^2,b=-2x,c=3と置けば、(a+b+c)^5の形になりますね。
展開式の一般項は、
_5C_p\cdot _{5-p}C_q\cdot (x^2)^p\cdot(-2x)^q\cdot 3^r= _5C_p\cdot _{5-p}C_q\cdot(-2)^q\cdot 3^r\cdot x^{2p}\cdot x^q = _5C_p\cdot _{5-p}C_q\cdot(-2)^q\cdot 3^r\cdot x^{2p+q}(ただしp,q,rは負でない整数で、p+q+r=nを満たす)
x^4の項は、2p+q=4のときですが、
これを満たすpとqの組み合わせは、1つじゃないんですね。
- p=0だと、q=4。このときr=1
- p=1だと、q=2。このときr=2
- p=2だと、q=0。このときr=3
の3パターンが存在します。
pが3以上だと2p+qが4を超えてしまうので、無しですね。
 粗茶さん
粗茶さんrの値はp+q+r=5から求めます。
x^4の項は、2p+1=4のときなので、p,q,rの組み合わせは、
(p,q,r)={\color{red}(0,4,1)},{\color{blue}(1,2,2)},{\color{green}(2,0,3)}がある。
よって求める係数は、
\begin{array}{ll}
&{\color{red}_5C_0\cdot_{5-0}C_4\cdot(-2)^4\cdot 3^1}+{\color{blue}_5C_1\cdot_{5-1}C_2\cdot(-2)^2\cdot 3^2}+{\color{green}_5C_2\cdot_{5-2}C_0\cdot(-2)^0\cdot 3^3}\\\\
=&_5C_0\cdot_5C_4\cdot 16\cdot 3+_5C_1\cdot_{4}C_2\cdot 4\cdot 9+_5C_2\cdot_{3}C_0\cdot 1\cdot 27\\\\
=&1\cdot 5\cdot 16\cdot 3+5\cdot 6\cdot 4\cdot 9+10\cdot 1\cdot 1\cdot 27\\\\
=&240+1080+270\\\\
=&1590
\end{array} 学生の方
学生の方なんで3つ足したの?
最後に3つの数字を足す理由に疑問を持った人も多いかもしれません。
今の問題で説明すると、次のようになります。
\color{red}p=0,q=4,r=1…4つの括弧から-2x、1つの括弧から3を選んでかけてできる項を全部足すと240x^4になる。
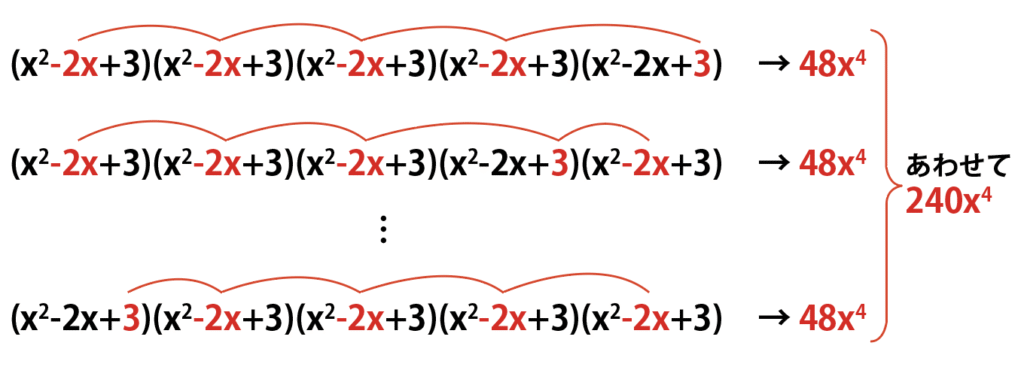
\color{blue}p=1,q=2,r=2…1つの括弧からx^2、2つの括弧から-2x、2つの括弧から3を選んでかけてできる項を全部足すと1080x^4になる。
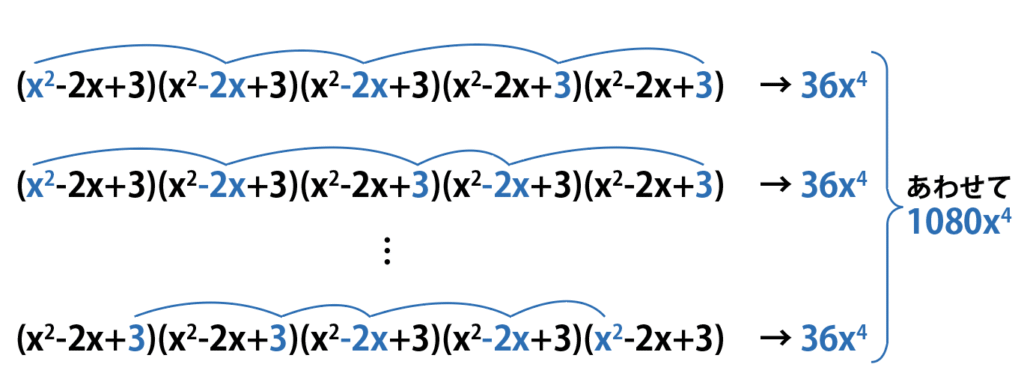
\color{green}p=2,q=0,r=3…2つの括弧からx^2、3つの括弧から3を選んでかけてできる項を全部足すと270x^4になる。
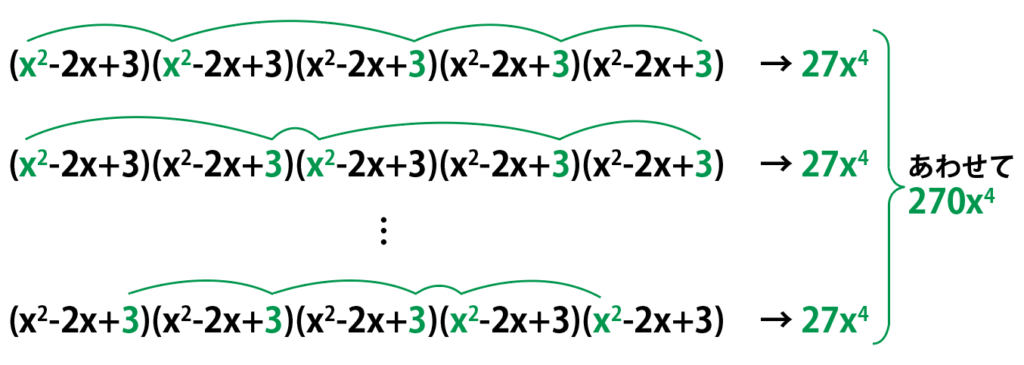
最終的に同類項はまとめられるので、全部足されて、
240x^4+1080x^4+270x^4=1590x^4
ということになります。
括弧の中に同じ文字(x^2と-2xのように)が含まれている展開の場合、このように同類項が出てくることがあるので、覚えておきましょう。
まとめ
この記事では、二項定理の式の成り立ちの理由と、二項定理を用いた係数の問題について解説しました。
超頻出分野というほどではないですが、学校の実力テストや入試問題でも小問として少しだけ出題されることがらではあるので、解き方はしっかり覚えておきたいですね!
このブログでは,自分で勉強しているとき,つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や,勉強が楽しくなる文房具も紹介していますので,よろしければご覧ください!



