「位置ベクトル」を学習すると出てくる,「交点の位置ベクトル」の問題。
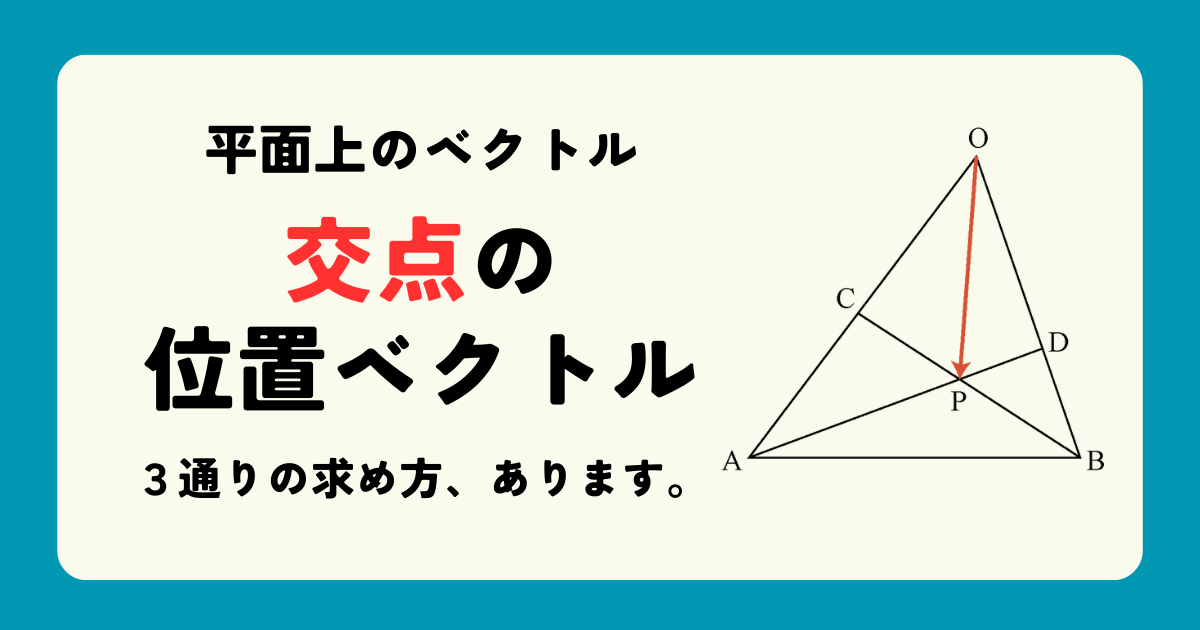
図だとこれです。
このときの\rm \overrightarrow{OP}を求めよ。っていう問題。
教科書ではsとtをおいて連立方程式を作って解く方法を習いますが,
実は連立方程式を使わずに,交点の位置ベクトルを求める方法があります。
この記事では,交点の位置ベクトルの求め方を3種類紹介します。
お友達が連立方程式をめんどくさそうに解いているのを横目に,自分はスマートな方法でさっさと解いてしまい,優越感を味わいましょう!

粗茶
- 文系に特化して数学を分かりやすく教える高校数学の専門家
- 指導歴15年
- 数学が苦手で何から始めたらいいか分からない文系高校生の悩みを解決するコンテンツを展開しています。

交点の位置ベクトルの問題の解き方3選
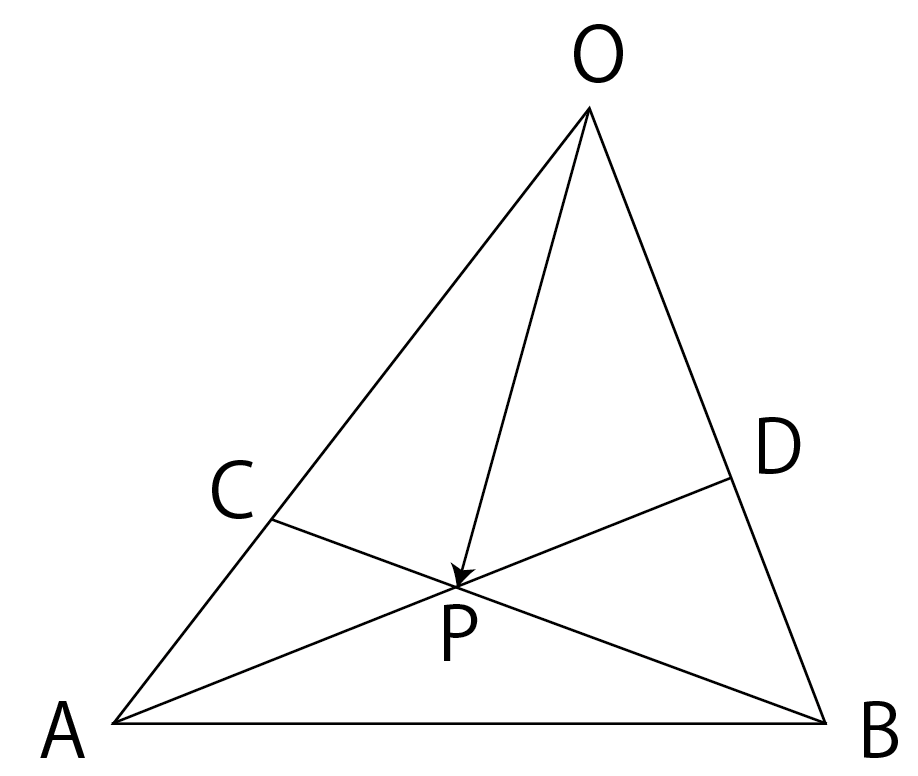
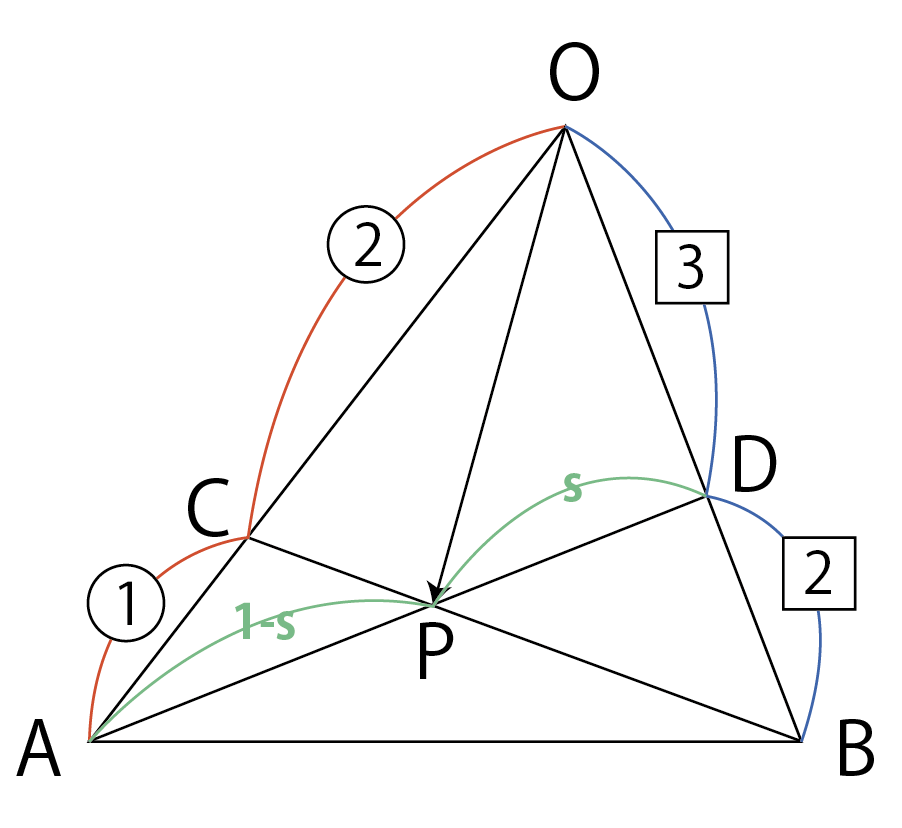
今回扱う問題はこちら。
三角形\rm ABCについて,辺\rm OAを2:1に内分する点を\rm C,辺\rm OBを3:2に内分する点を\rm Dとする。2つの線分\rm ADと\rm BCの交点を\rm Pとするとき,\overrightarrow{\rm OP}を\overrightarrow{\rm OA}と\overrightarrow{\rm OB}で表せ。
図示するとこんな感じ。
わかっている比を利用して,\overrightarrow{\rm OP}を\overrightarrow{\rm OA}と\overrightarrow{\rm OB}で表してね。という問題です。
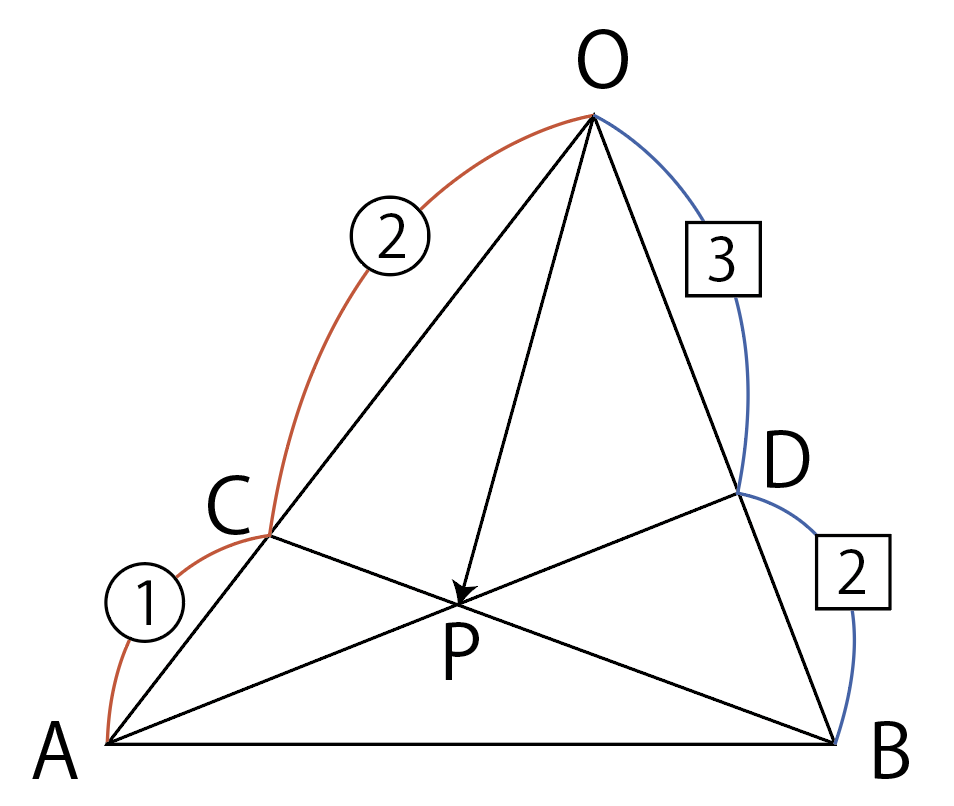
この問題の解き方を3種類紹介します。
- 教科書的方法(連立方程式を解く)
- 1つの文字で解く方法
- 文字を使わない方法(メネラウスの定理を使う)
それでは順に紹介していきます。
教科書的な方法(連立方程式)
交点の位置ベクトルの問題,教科書では連立方程式を解く方法が載っています。
\overrightarrow{\rm OP}を,文字を使って2種類の式で表します。
\rm Pは,\rm AD上にあるので,
{\rm AP:PD}=(1-s):sとおけます。
また,\rm Pは,\rm CB上にもあるので,
{\rm CP:PB}=(1-t):tとおけます。
 粗茶さん
粗茶さん{\rm AP:PD}=(1-s):sじゃなくて,{\rm AP:PD}=s:(1-s)でもOK。tも同様。
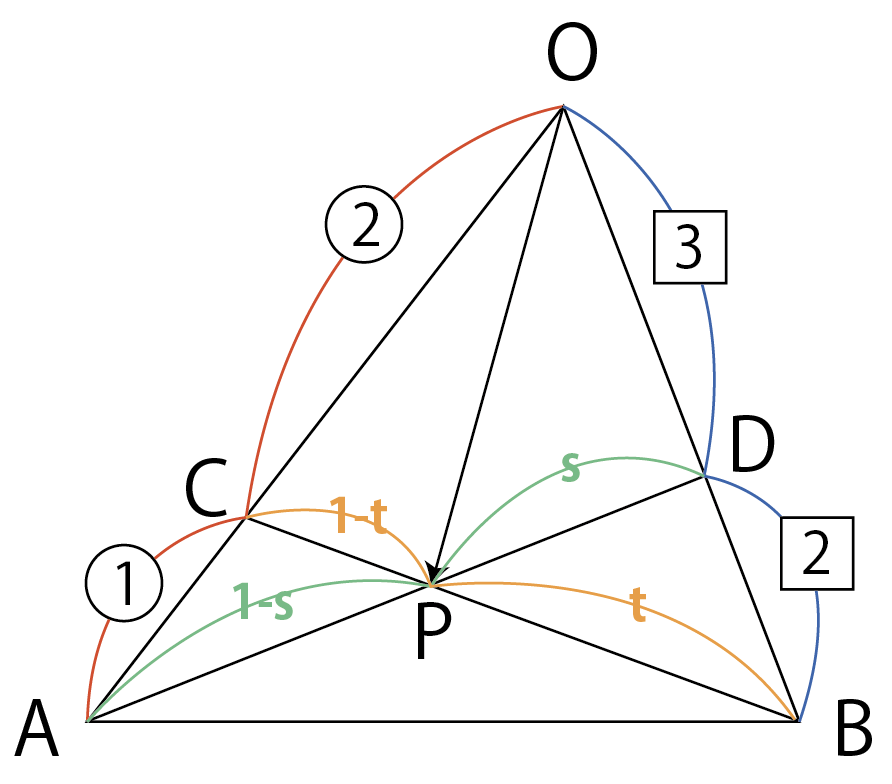
{\rm AP:PD}=(1-s):sより,
\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+(1-s)\overrightarrow{\rm OD}
\therefore \overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+\cfrac{3}{5}(1-s)\overrightarrow{\rm OB} …①
 粗茶さん
粗茶さん\rm OD:DB=3:2だから,\overrightarrow{\rm OD}=\cfrac{3}{5}\overrightarrow{\rm OB}
また,
{\rm CP:PB}=(1-t):tより,
\overrightarrow{\rm OP}=t\overrightarrow{\rm OC}+(1-t)\overrightarrow{\rm OB}
\therefore \overrightarrow{\rm OP}=\cfrac{2}{3}t\overrightarrow{\rm OA}+(1-t)\overrightarrow{\rm OB} …②
 粗茶さん
粗茶さん\rm OC:CA=2:1だから,\overrightarrow{\rm OC}=\cfrac{2}{3}\overrightarrow{\rm OA}
①と②は同じベクトル\overrightarrow{\rm OP}を表しています。
同じということは,\overrightarrow{\rm OA}の係数どうしが等しいし,\overrightarrow{\rm OB}の係数どうしも等しくなる。
\overrightarrow{\rm OA}と\overrightarrow{\rm OB}は一次独立なので,各係数を比較して,
s=\cfrac{2}{3}t…③
1-t=\cfrac{3}{5}(1-s)…④
 粗茶さん
粗茶さん\overrightarrow{\rm OA}と\overrightarrow{\rm OB}が平行でもなければ\overrightarrow{0}でもないことを「\overrightarrow{\rm OA}と\overrightarrow{\rm OB}は一次独立である」といいます。
係数の比較ができるのは,一次独立のときだけ。
③,④を連立させて解きましょう。
③を④に代入して,
1-t=\cfrac{3}{5}\left(1-\cfrac{2}{3}t\right)
⇔ -\cfrac{3}{5}t=-\cfrac{2}{5}
∴ t=\cfrac{2}{3}
③に代入して,
s=\cfrac{2}{3}\cdot\cfrac{2}{3}=\cfrac{4}{9}
sを①に代入して,
\overrightarrow{\rm OP}=\cfrac{4}{9}\overrightarrow{\rm OA}+\cfrac{3}{5}\left(1-\cfrac{4}{9}\right)\overrightarrow{\rm OB}
\therefore \overrightarrow{\rm OP}=\cfrac{4}{9}\overrightarrow{\rm OA}+\cfrac{1}{3}\overrightarrow{\rm OB} …(答)
これで何の問題もないのですが…
 学生の方
学生の方連立方程式めんどくさい。分数の計算やりたくない。
連立方程式になるし,ほぼ間違いなく分母の異なる分数が出てきます。
次は,連立方程式を使わず,文字1つで終わらせる方法を紹介します。
1つの文字で解く方法
交点の位置ベクトルを,1つの文字だけで求める方法です。
連立方程式になる場合は,sとtの2つを使いましたが,今回はsだけをおきます。
(tでもいいです)
\rm Pは,\rm AD上にあるので,
{\rm AP:PD}=(1-s):sとおけます。
{\rm AP:PD}=(1-s):sより,
\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+(1-s)\overrightarrow{\rm OD} …①
 粗茶さん
粗茶さんここまでは,tをおいていないだけで,連立方程式のときの同じ流れです。
ここで,点\rm Pは\rm CB上にもあるので,\overrightarrow{\rm OP}を\overrightarrow{\rm OC}と\overrightarrow{\rm OB}で表すことを考えます。
\overrightarrow{\rm OC}=\cfrac{2}{3}\overrightarrow{\rm OA}より,\overrightarrow{\rm OA}=\cfrac{3}{2}\overrightarrow{\rm OC}
\overrightarrow{\rm OD}=\cfrac{3}{5}\overrightarrow{\rm OB}
これらを①に代入して,
\overrightarrow{\rm OP}=\cfrac{3}{2}s\overrightarrow{\rm OC}+\cfrac{3(1-s)}{5}\overrightarrow{\rm OB}
さらにここで,直線上の点に関する超重要なことがあります。
直線{\rm AB}上に点\rm Pがあるとき,
\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB},
s+t=1(係数の和が1)
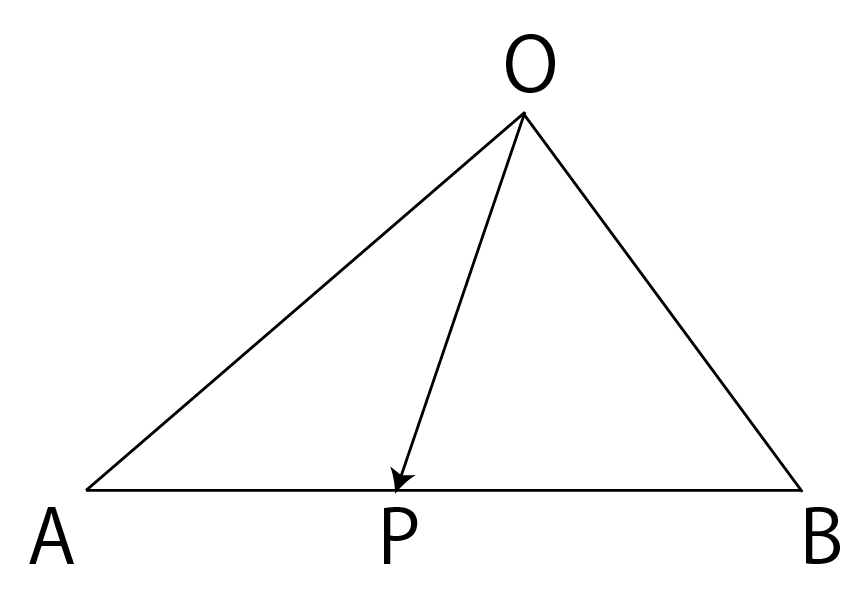
今回は,点\rm Pが\rm CB上にあるので,
\overrightarrow{\rm OC}の係数\cfrac{3}{2}sと\overrightarrow{\rm OB}の係数\cfrac{3(1-s)}{5}の和が1になります。つまり,
\cfrac{3}{2}s+\cfrac{3(1-s)}{5}=1
⇔15s+6(1-s)=10
∴s=\cfrac{4}{9}
①に代入して計算すると,
\overrightarrow{\rm OP}=\cfrac{4}{9}\overrightarrow{\rm OA}+\cfrac{5}{9}\overrightarrow{\rm OD}
\overrightarrow{\rm OD}=\cfrac{3}{5}\overrightarrow{\rm OB} だったので,
\overrightarrow{\rm OP}=\cfrac{4}{9}\overrightarrow{\rm OA}+\cfrac{5}{9}\cdot\cfrac{3}{5}\overrightarrow{\rm OB}
∴\overrightarrow{\rm OP}=\cfrac{4}{9}\overrightarrow{\rm OA}+\cfrac{1}{3}\overrightarrow{\rm OB} …(答)
 粗茶さん
粗茶さん「係数の和が1」は,位置ベクトルでは非常に重要なので,使いこなせるようにしておきたい!
文字をおかない方法(メネラウスの定理の利用)
 学生の方
学生の方結局AP:PDが分かればいいんじゃないの?
と思ったアナタは正解です。
AP:PD(またはCP:PB)がわかりさえすれば,\overrightarrow{\rm OP}を求めることができます。
ベクトルを使わない方法として,メネラウスの定理を使うこともできます。
図のように,三角形\rm OADと直線\rm CBがあるとき,
\rm \cfrac{AP}{PD}\cdot\cfrac{DB}{BO}\cdot\cfrac{OC}{CA}=1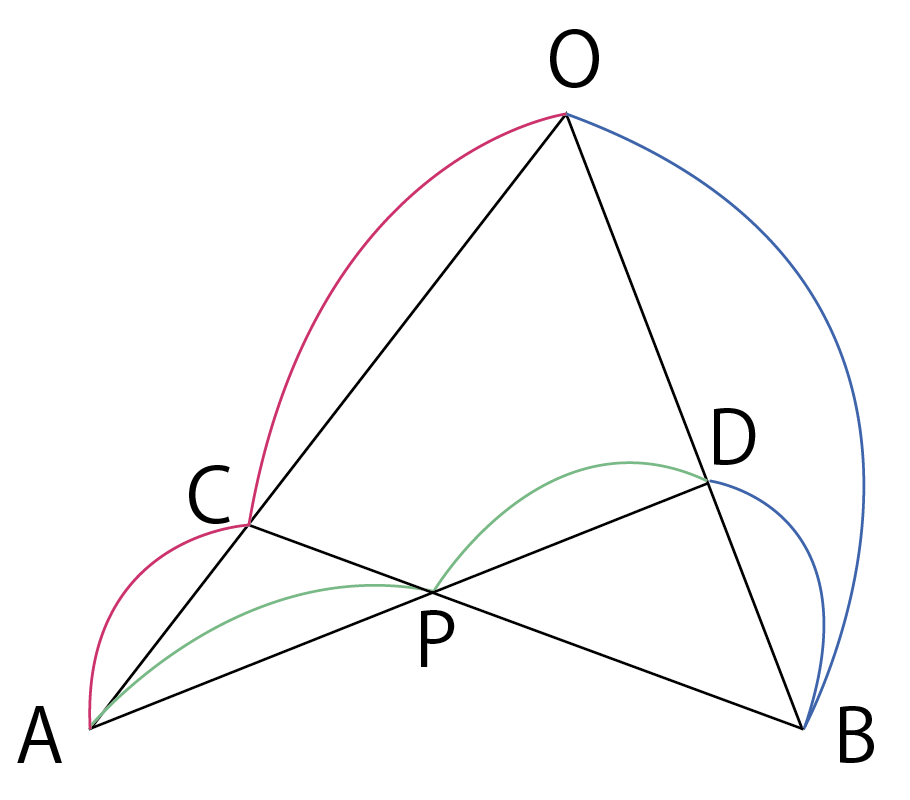
定理の説明は長くなるのでこの記事では省きますが,
メネラウスの定理を使うことで,AP:PDの比を求めることができてしまいます。
ここから解答。
メネラウスの定理より,
\rm \cfrac{AP}{PD}\cdot\cfrac{DB}{BO}\cdot\cfrac{OC}{CA}=1
それぞれの比を代入して,
\rm \cfrac{AP}{PD}\cdot\cfrac{2}{5}\cdot\cfrac{2}{1}=1
∴\rm \cfrac{AP}{PD}=\cdot\cfrac{5}{4}
つまり,\rm AP:PD=5:4
\rm Pは\rm ADを5:4に内分するので,
\rm \overrightarrow{OP}=\cfrac{4}{9}\overrightarrow{OA}+\cfrac{5}{9}\overrightarrow{OD}
\overrightarrow{\rm OD}=\cfrac{3}{5}\overrightarrow{\rm OB} だったので,
\overrightarrow{\rm OP}=\cfrac{4}{9}\overrightarrow{\rm OA}+\cfrac{5}{9}\cdot\cfrac{3}{5}\overrightarrow{\rm OB}
∴\overrightarrow{\rm OP}=\cfrac{4}{9}\overrightarrow{\rm OA}+\cfrac{1}{3}\overrightarrow{\rm OB} …(答)
このようにして,比がわかりさえすればいいので,メネラウスの定理を使う方法も有効です。
というか,けっこうオススメです。
交点の位置ベクトル まとめ
交点の位置ベクトルの求め方を3通り紹介しました。
- 連立方程式でやる(教科書的)
- 1つの文字でやる
- メネラウスの定理で比を求める
「AP:PD(または「CP:PB)を求める」という目的はすべて同じです。
基本的には好きな方法でやってもらっていいのですが,
共通テストなどの穴埋め形式の問題の場合は,連立方程式の方法を指定されることがあります。
複数の方法で導けるようにしておきましょう。
このブログでは,自分で勉強しているとき,つまづきやすいポイントを解説。
「かゆいところに手が届く」情報を発信しています。
自分で勉強する際にオススメの参考書や,勉強が楽しくなる文房具も紹介していますので,よろしければご覧ください!